모두의 연구소 - 아이펠 리서치 과정 3주차 (2)

알파고라니·2023년 10월 1일

aiffel

목록 보기

4/15

3주차

3주차에 학습한 내용이 많기 때문에 앞선 포스팅과 3-2주차 포스팅을 나누어서 정리했다!

" 3주차 두번째 포스팅 내용"
6. 확률과 확률분포
7. likelihood와 MLE
8. 정보이론(information theory)
9. 비지도 학습(unsupervised learning)
10. 추천 시스템 기초 with sklearn

6. 확률과 확률 분포

딥러닝은 결정론적인 것이 아닌 확률적인 것을 기반으로 결과를 도출한다.
그렇다면 확률은 무엇일까?

6.1 확률이란?

확률을 알기 위해서는 여러 단어에 익숙해 질 필요가 있다.

우선 시행(random experiment)에 대해 알아야하는데,
시행은 같은 조건 하에서 여러 번 반복할 수 있는 어떤 실험에서, 결과를 알 수는 없지만 일어날 가능성이 있는 모든 결과를 사전에 알 수 있는 실험을 의미한다.

시행에서 일어날 수 있는 모든 가능성의 결과를 원소로하는 집합을 표본 공간(sample space)라고 한다.
예를 들어 주사위 던지기의 표본 공간은 A = {1, 2, 3, 4, 5, 6}으로 표현할 수 있다.

여기서 표본 공간을 구성하는 집합 원소가 이산적이면(discrete) 이산 표본 공간, 연속적이면(continuous) 연속 표본 공간이라고 표현한다.

이러한 표본 공간에서 특정한 규칙에 의해 정해진 결과의 부분 집합을 사건(event)이라고 한다.
주사위 던지기 예에서 짝수가 나올 경우의 집합과 같은 것이 사건에 해당된다.
짝수가 나올 경우 = {2, 4, 6}

수학적으로 확률은 다음과 같이 표현된다.
표본 공간 A에서 사건 B가 발생할 확률 = P(B).
위의 짝수가 나올 확률은 3/6 = 1/2가 될 것이다.

6.2 조건부 확률

확률이 0이 아닌 두 사건 A,B에 대해서 사건 A가 일어났을 때 사건 B가 일어날 확률을 사건 A가 일어났을 때 사건 B의 조건부 확률이라고 한다.
$P(B|A)$ 로 표현하며, $P(B|A) = {P(B∩A) \over P(A)}$ 와 같이 정의된다.

다시 주사위 던지기 예시로 돌아가보자.
첫번째 주사위가 4일 때, 두 주사위의 합이 7이 되는 확률은 어떻게 구할 수 있을까? 우선 4가 먼저 나올 경우는 (4,1), (4,2), (4,3), (4,4), (4,5), (4,6)의 6가지 경우이다. 두 주사위를 던지는 것을 감안하면 $6 \over 36$ 이다.

조건부 확률에 의하면 4가 나오는 사건을 A라고 하고, 두 수의 합이 7이 되는 사건을 B라고 하자.
이에 따라 다음과 같이 정리할 수 있다.

$P(B|A)={P((4,3)) \over P((4,1))+P((4,2))+P((4,3))+P((4,4))+P((4,5))+P((4,6))}$

= $(1/36)\over(6/36)$

= $1 \over 6$

6.3 확률 변수

어떤 시행에 대한 표본 공간 A의 한 표본 점을 B라고 하면, B를 하나의 실수에 대응시키는 것(함수와 같은 역할)을 확률 변수(random variables)라고 한다.

예를 들어 2개의 동전을 차례대로 던진다고 할 때 나올 경우의 수는 다음과 같다.
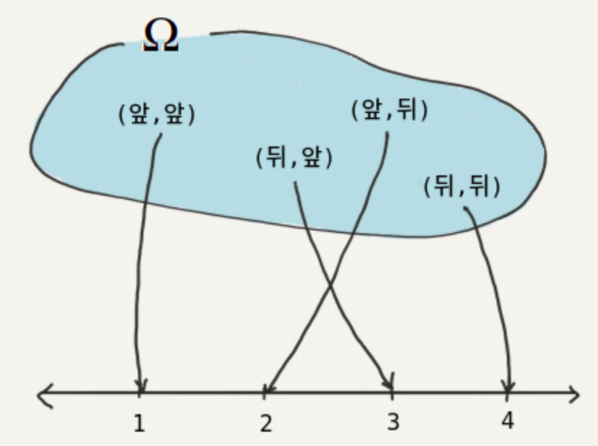
(앞,앞), (앞,뒤), (뒤,앞), (뒤,뒤)

이를 실수 1,2,3,4에 대응시키면(확률 변수로 표현하면)
X( (앞,앞)=1, (앞,뒤)=2, (뒤,앞)=3, (뒤,뒤) = 4 )

6.3 확률 분포

확률 분포는 어떤 사건이 일어날 가능성을 나타내는 수학적 모델로, 확률 변수라고 불리는 변수에 대한 가능한 값들과 그 값들이 나타날 확률을 정의한다.
이러한 분포는 이산적인 경우와 연속적인 경우로 나눌 수 있다.

앞서 언급한 것과 같이 여기서 표본 공간을 구성하는 집합 원소가
이산적이면(discrete) 이산 표본 공간 -> 이산 표본 분포,
연속적이면(continuous) 연속 표본 공간 -> 연속 표본 분포

1. 이산 확률 분포(Discrete Probability Distribution)

확률 변수가 이산적인 값을 가질 때 사용 된다.
확률 질량 함수(Probability Mass Function, PMF): 각 값에 대한 확률을 나타내는 함수
EX)
이항 분포, 포아송 분포 등
주사위의 눈금, 동전을 던졌을 때의 앞면, 뒷면, 로또의 당첨 번호 등

2. 연속 확률 분포(Continuous Probability Distribution)

확률 변수가 연속적인 값을 가질 때 사용 됨
확률 밀도 함수: 확률 변수의 특정 값에 대한 확률은 구간에 대한 적분으로 나타내는 함수
EX)
정규 분포, 균등 분포 등
사람의 키, 몸무게, 온도 등

7. likelihood와 MLE

Likelihood는 데이터가 주어졌을때 분포가 데이터를 얼마나 잘 설명하는가를 나타낸다.
이를 이해하기 위해서는 probability(확률)과 likelihood(우도)를 구분지어 비교할 필요가 있다.

확률 (=확률밀도함수의 면적)

고양이 몸무게를 예시로 이해해보면,

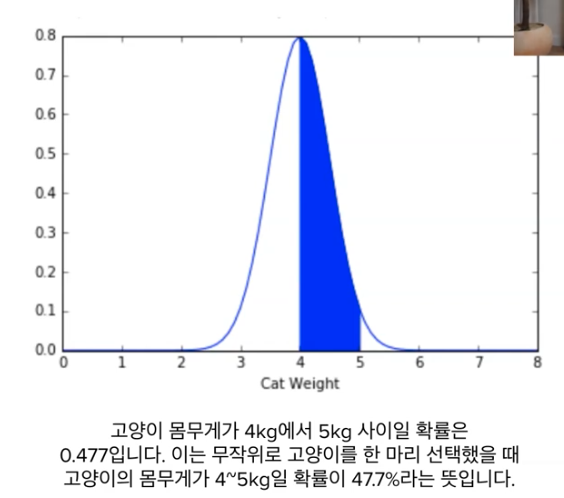
평균이 4 표준편차가 0.5를 따르는 확률 분포가 있다고 하면,
고양이 몸무게가 4~5kg일 확률은 47.7%이다.
이는 연속확률분포에서 확률밀도함수의 면적을 구하면 47.7이 나오기 때문이다.

즉, 여기선 입력 데이터는 변하지만 분포는 고정되어 있는 상황 "확률"  
=> p(data|distribution) = probability**

우도 (=확률밀도함수의 y값)

같은 고양이 몸무게 예시로 이해해보자.

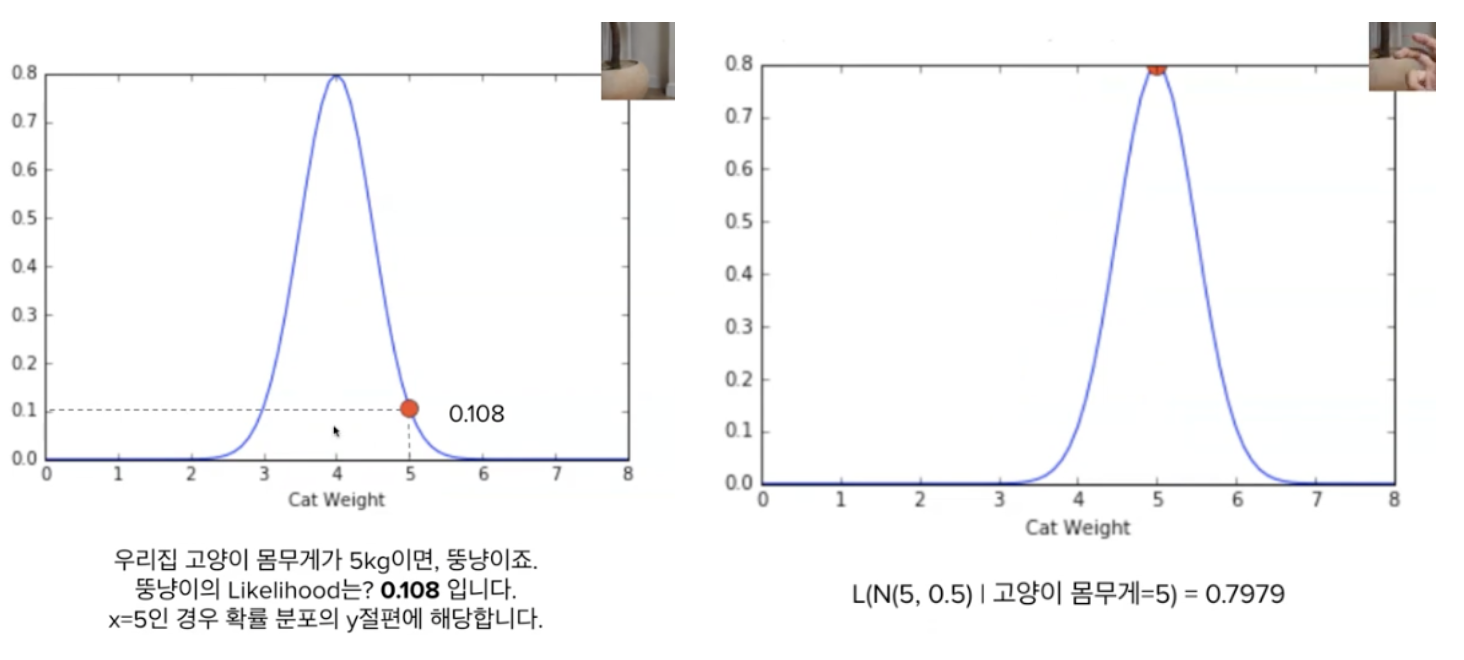
두 그림은 다른 확률 분포를 따른다.
고양이 몸무게가 5키로 인 경우 왼쪽의 likelihood는 0.108이다.
반면 오른쪽의 경우 0.7979이다.

즉, 좌측의 분포보다, 우측의 분포가 고양이 몸무게 5키로를 더 잘 설명한다. (=발생가능성이 더 높다)

이것이 의미하는 것은 다음과 같다.

입력 데이터는 고정되어있지만 분포는 변하는 상황에서 (=데이터가 주어졌을때)
분포가 데이터를 얼마나 잘 설명하는가를 의미한다.

MLE

머신러닝에서 우리가 구하고 싶은 것은 모델의 파라미터 값이다. 앞서 살펴본 것처럼 데이터는 고정된 값이기 때문에 파라미터 확률 분포를 모델이 잘 표현하도록 하는 것이 필요하기 때문이다.

위의 예시에서 알 수 있듯이 likelihood가 높다는 것은 학습된 파라미터 조건에서 데이터가 관찰될 확률이 높다는 것이고, 데이터 분포를 모델이 잘 표현한다고 할 수 있다.
이렇게 데이터들의 likelihood 값을 최대화하는 방향으로 모델을 학습시키는 방법을 최대 가능도 추정(MLE)이라고 한다.

우도 영상자료