
0. Intro
Stanford University의 CS231n 강의를 듣고 정리한 내용입니다.
궁금한 점이나 오류가 있다면 언제든지 댓글 남겨주시기 바랍니다.
1. Loss Functions
1) Definition of Loss Function
The loss function quantifes our unhappiness with predictions on the training set.
Loss function이란 기본적으로 우리의 classifier가 얼마나 잘 작동하고 있는 지를 나타내 주는 척도라고 생각하면 된다.
이름에서 알 수 있듯이 직관적으로 loss값이 크다면 그만큼 classifier가 잘 작동하지 못 하고 있음을 의미한다.
위의 식에서 볼 수 있듯이 각각의 example 별 loss 값을 계산한 뒤 평균을 내서 최종적인 loss 값을 산출한다.
2) Multiclass of SVM Loss - Hinge Loss
SVM(Support Vector Machine)이란 분류 문제에서 decision boundary를 설정할 때 데이터군으로부터 최대한 멀리 떨어지게끔 하는 분류 방법론을 뜻한다. 여기서는 SVM의 loss값을 주로 얘기할 예정이라 더 자세히는 다루지 못 하고 간단히만 설명하고자 한다.
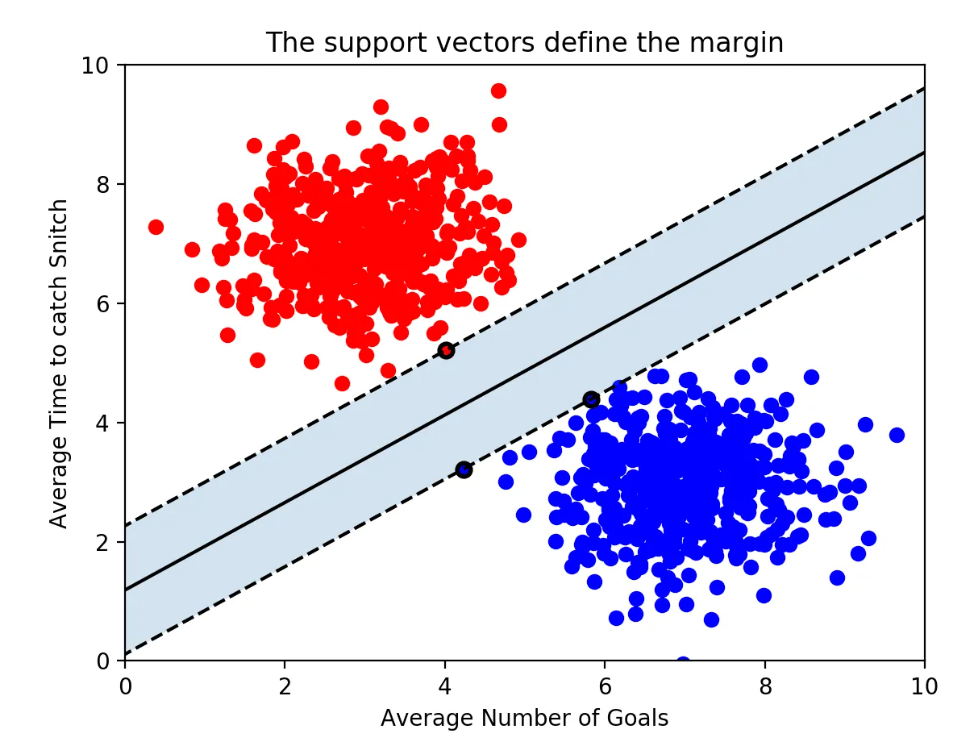
위의 그림에서 decision boundary와 가장 가까이 있는 각 그룹별 데이터를 support vector라고 한다. 이 support vector와 decision boundary 사이의 거리를 margin이라고 한다. 이 margin을 최대화 하는 것이 SVM의 목표라고 할 수 있다.
SVM을 다항 분류기로도 사용할 수 있는데 이것을 multiclass SVM이라고 하며 여기서 사용되는 loss function이 hinge loss이다.
Hinge loss를 살펴보기 전에 먼저 위의 예제를 보면서 이해해 보도록 하자. Classifier에 image를 넣었을 때 각 class 별 점수가 산출된다.

위의 그림을 보면 input 값으로 고양이 사진을 넣었을 때 각 class 별 점수는 다음과 같다.
- cat : 3.2
- car : 5.1,
- frog : -1.7
우리의 classifier는 이들 중 가장 높은 값을 지니는 class로 이미지를 분류하기 때문에 실제 정답 class인 cat보다 car의 점수가 더 높기 때문에 위의 예제에선 classifier가 잘 분류하고 있지 못 함을 알 수 있다.
이미지의 실제 label을 라고 하자. 인 나머지 class에 대해서 조사했을 때 classifer가 잘 작동한다는 것은 정답인 가 정답이 아닌 보다 더 커야한다. 이때 미리 정해둔 safety margin만큼의 여유를 두고 가 보다 크도록 하는 것이 SVM loss의 목표이다.
The Multiclass Support Vector Machine "wants" the score of the correct class to be higher than all other scores by at least a margin of delta.

Hinge loss는 이 점을 활용해서 계산된다. 이라면 옳바르게 분류한 것이기 때문에 이 된다. 반면에 그렇지 못하다면 그 차이인 만큼이 loss가 되는 것이다.

이런 방식으로 example에 대한 loss를 각각 구한 뒤 이것을 평균내어 최종 loss 값을 산출한다.
Sanity Check
Sanitiy check는 hinge loss의 다음과 같은 성질을 이용해서 학습 초기에 debug 할 때 사용하는 방식이다. 맨 처음 학습 때 가중치는 매우 작게 설정되기 때문에 모든 s 값이 0에 근사하게 된다. 이때 loss 값을 계산해보면 는 인 경우에서 각각 미리 설정된 margin만큼 loss가 발생하게 된다. 그것들의 합은 margin (# of classes - 1) 이 된다. 모든 example에서 같은 값이 발생함으로 최종 loss = margin ( # of classes - 1)이다.
만약에 margin을 1로 설정하였다면 초기에 loss 값이 # of classes - 1인지를 확인해보면서 디버깅을 하면 되는 것이다. 이를 sanity check라고 한다.
Squared hinge loss SVM (L2-SVM)
Squared hinge loss SVM 은 말그대로 기존의 hinge loss의 squared version이라고 생각하면 된다. 그 형태는 으로 표현된다. Unsquared version과는 차이가 있으나 어떤 형태가 더 알맞을 지는 cross-validation을 통해서 결정해야 한다.
3) Regularization
Regularization에 대한 논의는 다음과 같은 문제의 발생으로 시작된다. 이 된다고 가정할 때 그때의 가중치 가 unique 하지 않는다는 점에서 문제가 발생한다.

을 만족시키는 가 있다고 했을 때 도 역시 이 된다. 그 이유는 이 변환이 모든 score 값에 대해서 uniformly하게 적용되기 때문이다.
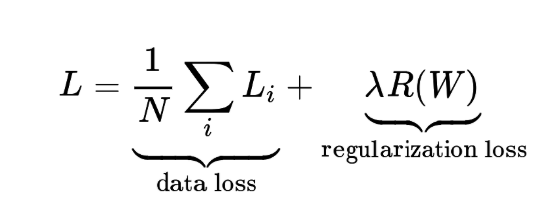
따라서 이러한 모호성을 해결하기 위해서 Loss function에 regularization term을 추가한다. 우선 앞서 봤던 loss는 data loss로 model이 training data 에 최적화 하는 것이 목표이다. 반면에 regularization term은 data가 아니라 오로지 가중치에만 기반한다. 이 항은 모델이 최대한 단순한 형태를 추구하며 test data에 잘 작동하는 것을 목표로 한다. 즉 regularization을 진행하면 진행할 수록 training error는 커지지만 test error는 감소하게 되는 효과를 볼 수 있다.
따라서 data loss와 regularization 사이의 trade off가 발생하기에 hyperparameter인 값을 cross-validation을 통해 조절하면서 적정 수준을 찾아나가야 한다.
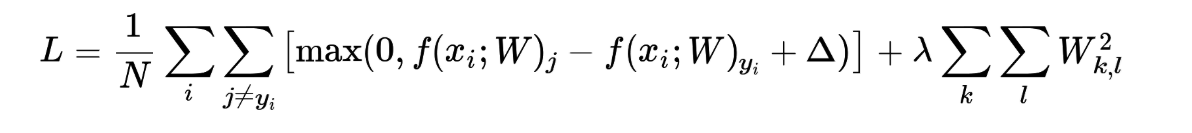

L2 regularization은 여러 regularization 방식 중 많이 사용되는 방식이다. 위의 결과에서도 볼 수 있듯이 L2 regularization은 가중치가 특정 값에만 영향을 주는 보다 모든 값에 영향을 주는 를 좀 더 선호한다. 따라서 L2 regularization을 진행하게 되면 가중치가 전반적으로 작고 분산된 형태로 가기 때문에 overfitting을 줄이고 test set에 대한 일반적인 성능을 향상시킬 수 있게 된다.
4) Softmax - Cross Entropy Loss
Softmax란 logistic regression의 다항 분류 version이며 softmax classifier를 통해 얻어진 score 값은 SVM과 다르게 확률적으로 해석할 수 있다. Softmax의 score에 대한 정의는 다음과 같다.
score = The unnormalized log probabilities for each class
Softmax에서는 cross-entropy loss를 loss function으로 사용하며 식은 다음과 같다.

Sanity check
SVM과 마찬가지로 sanity check를 진행할 수 있다. 초기에 W가 매우 작아 모든 s값이 거의 0에 가깝다고 할 때 그때의 loss 값은 다음과 같이 전개된다.
따라서 이 값을 이용해 sanity check를 진행할 수 있다.
2. Optimization
Optimization이란 기본적으로 loss를 최소화하는 weight를 찾아나가는 과정이라고 할 수 있다. Loss를 등고선의 형태로 표현하게 되면 다음과 같다.
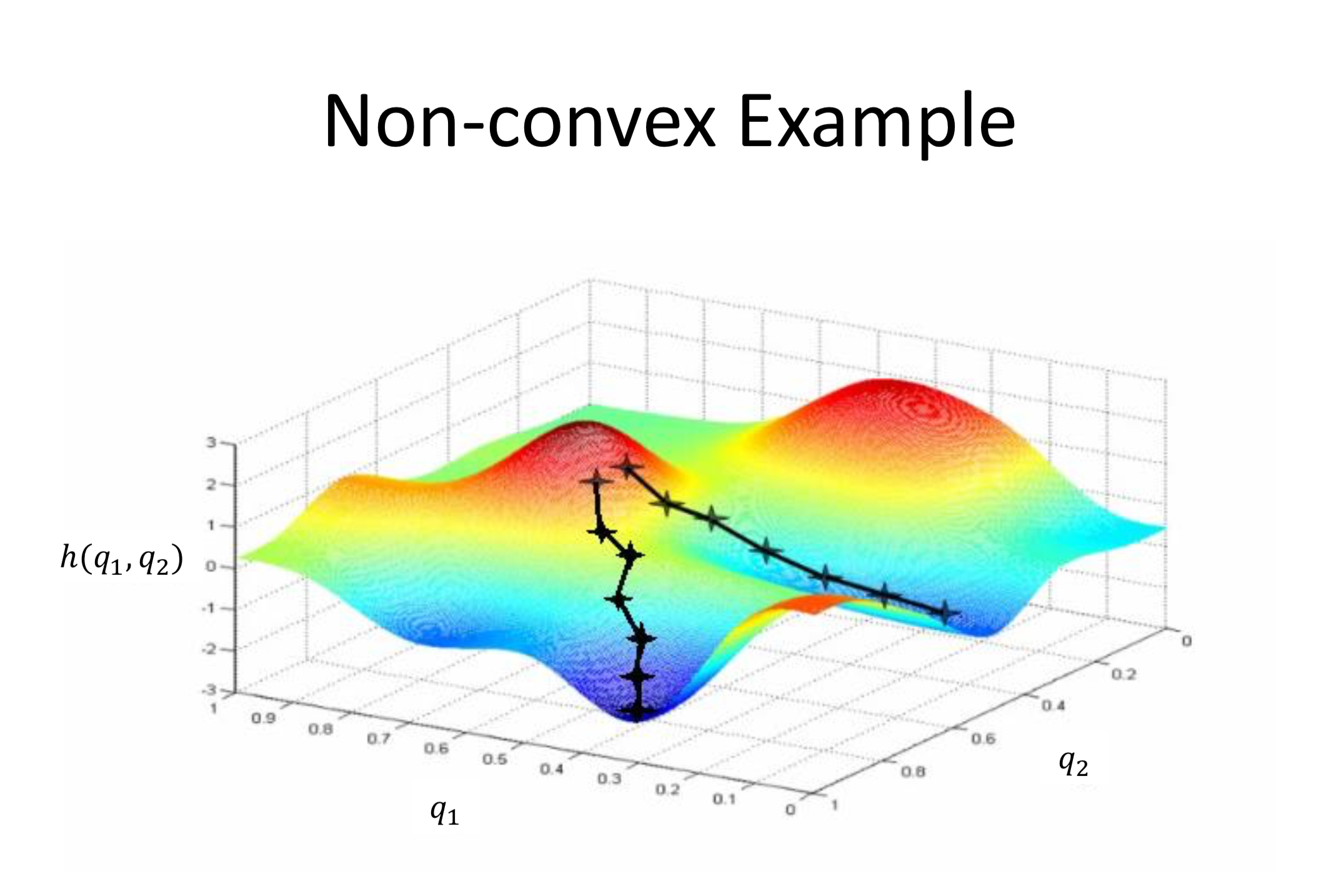
붉게 표현된 가장 높은 지점은 loss값이 가장 큰 지점이고 파랗게 표현된 가장 낮은 지점은 loss 값이 가장 낮은 지점이다. Optimization에서의 목표는 loss 값이 가장 낮은 지점을 찾아나가는 것이기 때문에 마치 산의 고지점에서 저지점을 향해 가는 형태와 비슷하다고 볼 수 있다.
Random Search
# assume X_train is the data where each column is an example (e.g. 3073 x 50,000)
# assume Y_train are the labels (e.g. 1D array of 50,000)
# assume the function L evaluates the loss function
bestloss = float("inf") # Python assigns the highest possible float value
for num in range(1000):
W = np.random.randn(10, 3073) * 0.0001 # generate random parameters
loss = L(X_train, Y_train, W) # get the loss over the entire training set
if loss < bestloss: # keep track of the best solution
bestloss = loss
bestW = W
print 'in attempt %d the loss was %f, best %f' % (num, loss, bestloss)
# prints:
# in attempt 0 the loss was 9.401632, best 9.401632
# in attempt 1 the loss was 8.959668, best 8.959668
# in attempt 2 the loss was 9.044034, best 8.959668
# in attempt 3 the loss was 9.278948, best 8.959668
# in attempt 4 the loss was 8.857370, best 8.857370
# in attempt 5 the loss was 8.943151, best 8.857370
# in attempt 6 the loss was 8.605604, best 8.605604
# ... (trunctated: continues for 1000 lines)그렇다면 어떻게 loss 값이 가장 작은 지점을 찾아낼 수 있는 지가 문제가 된다. 기본적으로 생각해 볼 수 있는 것은 Random Search인데 이를 통해 loss 값이 가장 작은 지점을 찾아내려는 방법은 성능이 매우 좋지 않다. 따라서 이러한 방식은 사용하면 안 된다.

그 다음 방식으로는 산 정상에서 하산하듯이 경사를 따라 내려가는 방식을 생각해 볼 수 있다. 상상해보자 산 정상에서 가장 빨리 하산하려면 내가 위치한 지점에서 가장 가파른 길로만 가면 된다. 이때 optimization에서 가파른 정도를 측정할 수 있는 값이 바로 gradient이다.
1) Gradient
Numerical Gradient
위의 식과 같이 계산하는 방식을 numerical gradient라고 한다. 컴퓨터에서 이를 구현할 때 h를 0에 가까운 매우 작은 값을 넣어 구한다.
코드 작성하기엔 쉽지만 근사치이며 모든 example에 대해서 이를 계산하는 것은 느리고 부담이 크다. 따라서 이 방식보다는 analytic gradient를 주로 활용하게 된다.
Analytic Gradient
Analytic gradient란 이미 알려진 미분법을 통해서 계산하는 방식이다. 따라서 정확하고 매우 빠르지만 error에 취약하다는 단점을 가지고 있다. 따라서 실제로 활용할 때 이 analytic gradient를 통해서 계산하고 numerical gradient를 통해 검산하는 방식을 취하는 데 이를 gradient check라고 한다.
Gradient Descent
이제 경사도를 찾았으니 내려가기만 하면 된다. 이를 gradient descent라고 부른다. 말그대로 경사를 따라 하강하는 방식이다.
Gradient descent의 기본적인 형태는 기존의 weight에서 weight의 gradient만큼을 뺀 값을 새로운 weight로 업데이트 한다. weight에서 gradient를 빼는 이유는 gradient의 반대 방향(negative gradient direction)으로 하강해야 하기 때문이다.
위 식에서 gradient 앞에 곱해진 step size는 learning rate라고도 불리는데 학습 정도를 결정하는 hyperparameter이다. Step size가 너무 작으면 학습이 더디고, 반대로 너무 크면 overshootting이 일어날 수 있기 때문에 cross-validation을 통해 적절한 step size를 잘 결정해야 한다.
Full Batch Gradient Descent
기본적인 gradient descent는 full batch gradient descent이다. 이는 gradient descent를 진행할 때 매 단계마다 모든 training examples을 이용하는 방식을 뜻한다.
# Vanilla Gradient Descent
while True:
weights_grad = evaluate_gradient(loss_fun, data, weights)
weights += - step_size * weights_grad # perform parameter updateMini-batch Gradent Descent
고차원의 data set에서 gradient descent를 진행하려고 할 때, full batch의 방식을 적용한다면 학습 시간이 너무 크게 소요된다는 단점이 있다. 매 학습마다 매우 큰 차원의 weight을 미분하고 update 하는 것은 사실 무리일 수 있다. 또한 거대한 data set을 메모리에 한번에 올리는 것 또한 불가능하다. 따라서 이러한 경우에 모든 example을 활용하는 것이 아니라 data set을 일정한 size로 나눈 mini-batch를 활용하는 방식을 사용한다.
# Vanilla Minibatch Gradient Descent
while True:
data_batch = sample_training_data(data, 256) # sample 256 examples
weights_grad = evaluate_gradient(loss_fun, data_batch, weights)
weights += - step_size * weights_grad # perform parameter update위의 코드를 보면 full-batch와는 다르게 sample_training_data를 256개로 쪼개서 활용하고 있는 것을 볼 수 있다. 이렇게 전체 학습 데이터를 일정한 batch size로 나눠 순차적으로 gradient descent를 진행하기 때문에 좀 더 빠르게 수렴할 수 있다는 장점이 있다.
Mini-batch의 size를 결정할 때 으로 결정하는 것이 좋다.
왜냐하면 vector 연산은 input size가 일 때 빠르기 때문이다.
Stochastic Gradient Descent (SGD)
mini-batch를 사용할 때 batch size가 1이라면 stochastic gradient descent라고 한다. 즉, 한 개의 데이터에 대해서만 gradient descent를 진행한다는 뜻인데 이렇게 되면 수렴 속도는 당연히 빠를 수 밖에 없지만 한 개의 데이터만 사용하기 때문에 병렬 연산에 강점을 보이는 gpu 자원을 낭비한다는 단점이 있다.
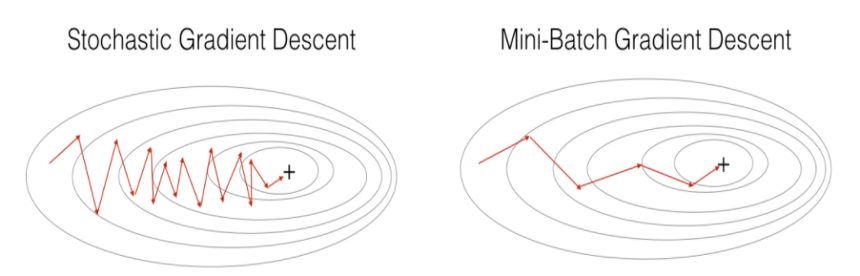
또 위의 그림처럼 shooting을 하면서 최저점을 찾아나가기 때문에 global minimum에 도달하지 못 할 수도 있다는 단점이 존재한다.
참고자료
CS231n youtube 강의
CS231n 강의노트
SVM 관련 블로그
Gradient Descent 관련 블로그
