0. Intro

Stanford University의 CS231n 강의를 듣고 정리한 내용입니다.
궁금한 점이나 오류가 있다면 언제든지 댓글 남겨주시기 바랍니다.

1. Gradient Descent & Backpropagation

1) Backpropagation을 사용하는 이유

지난 시간에 loss function을 이용해 optimization을 하며 이때 사용되는 방식이 gradient descent라고 배웠다. 즉 parameter를 업데이트 하기 위해서는 gradient, 즉 미분값이 필요하다. 간단한 모델에서는 analytic gradient을 손쉽게 구할 수 있지만 모델이 복잡해질 수록 한번에 미분하기는 어려울 것이다. 그래서 등장한 방식이 바로 Computational Graphs를 그려보는 것이다.

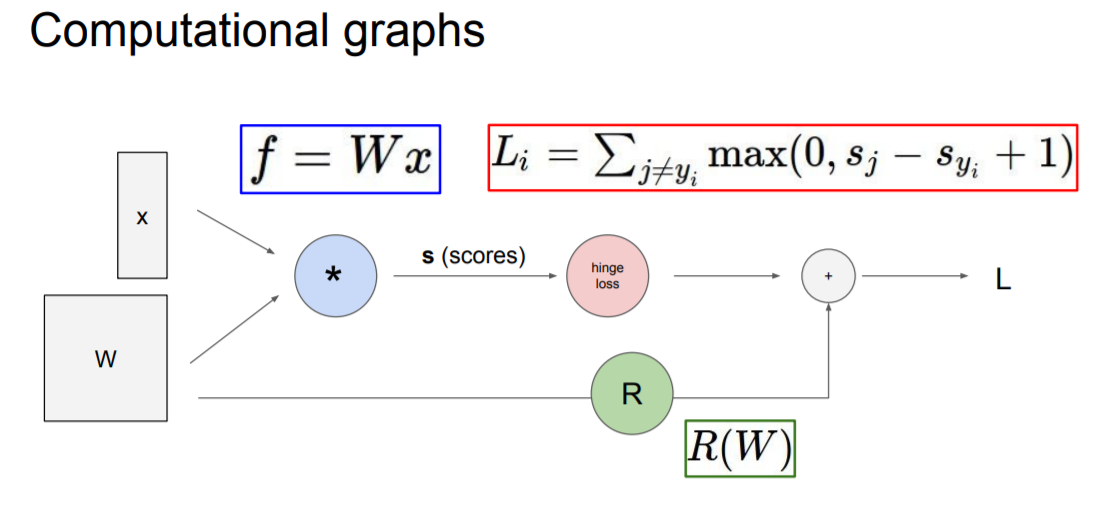
우선 지난 시간에 배운 hinge loss의 computational graphs 이다. 모든 연산과정을 세부적으로 나누어 표시한 것이다. 만일 모델이 여기서 더 복잡해진다면 다음과 같이 나타나기도 한다.

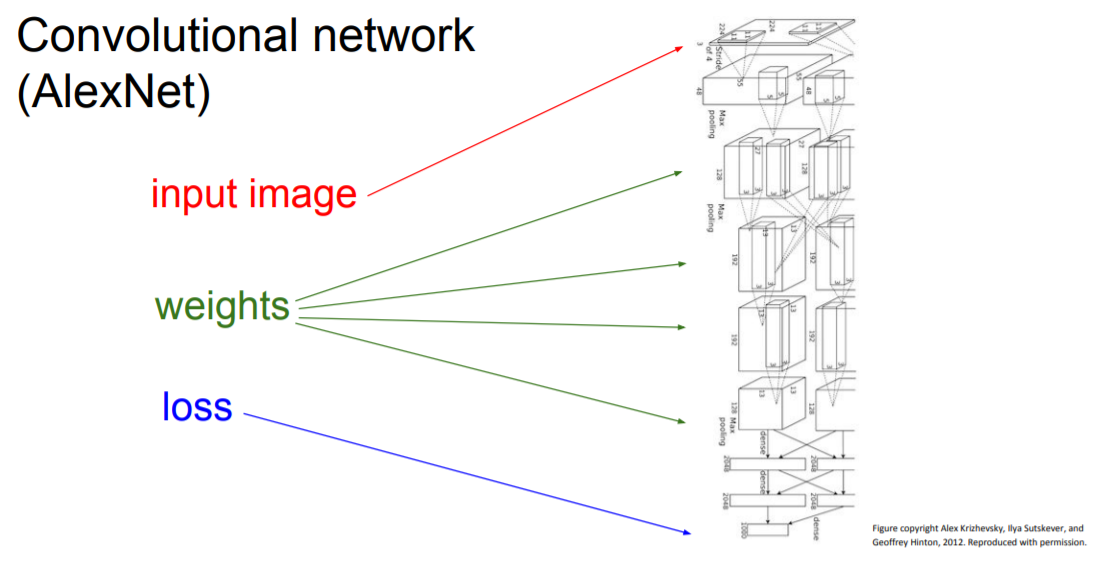
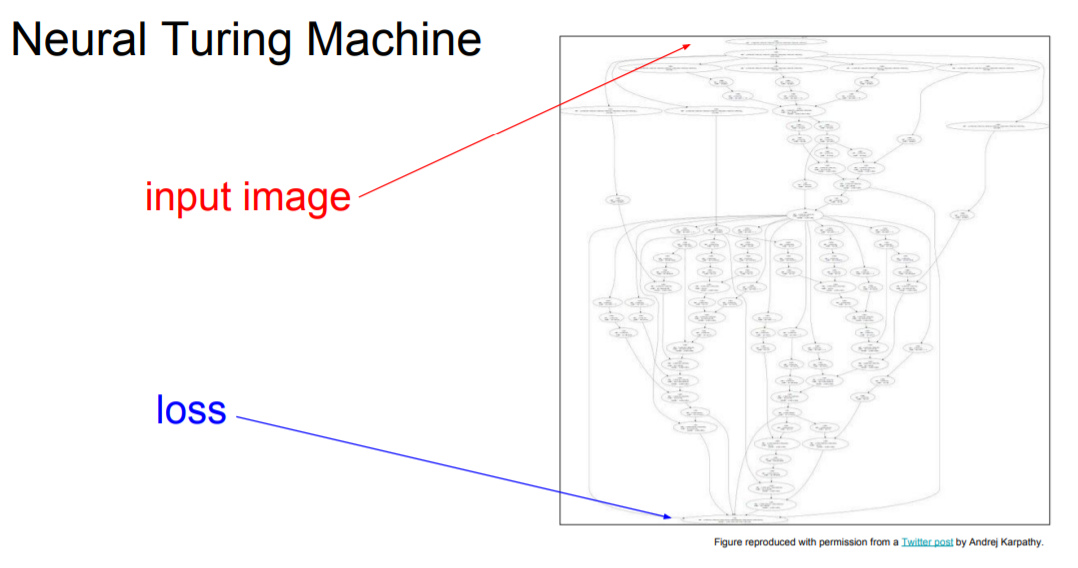
그렇다면 computational graphs를 그려가면서 세부적으로 나눈 것이 왜 gradient descent를 할 때 유용할까? 앞서 모델이 복잡해지면 미분하는데 시간이 오래 걸리고 복잡해진다고 했는데 computational graphs를 그리고 backpropagation을 진행하면 손쉽고 빠르게 미분을 할 수 있기 때문이다.

2) Backpropagation의 과정

간단한 예제를 보면서 backpropagation을 이해해보자.

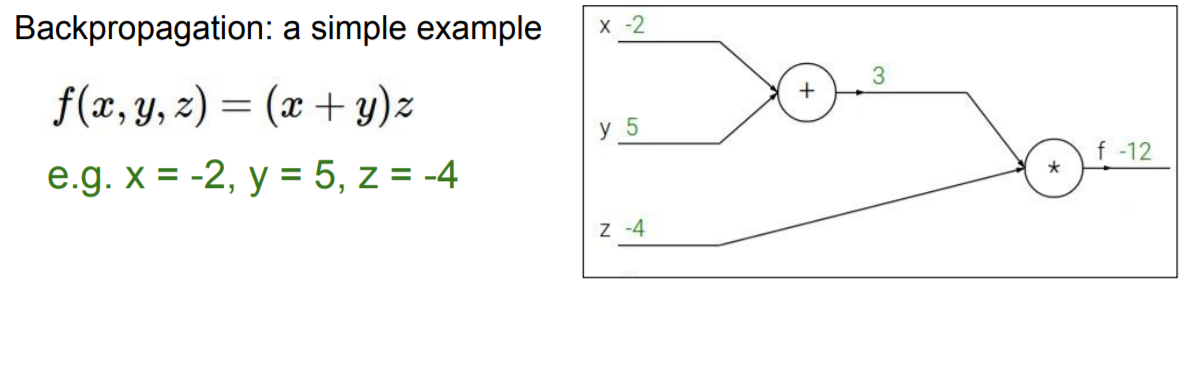
위와 같은 예제가 있다고 해보자. 우리의 목표는 각 parameter에 대한 편미분 값을 얻어 gradient descent를 진행하는 것이다.

우선 computational graph에서 순차적으로 값을 집어넣어 함수값을 구한다. 이를 forward pass라 한다.

그 이후엔 역방향으로 차례대로 미분을 하며 gradient를 구하는 데 이를 backward pass, 즉 backpropagation이라고 한다.

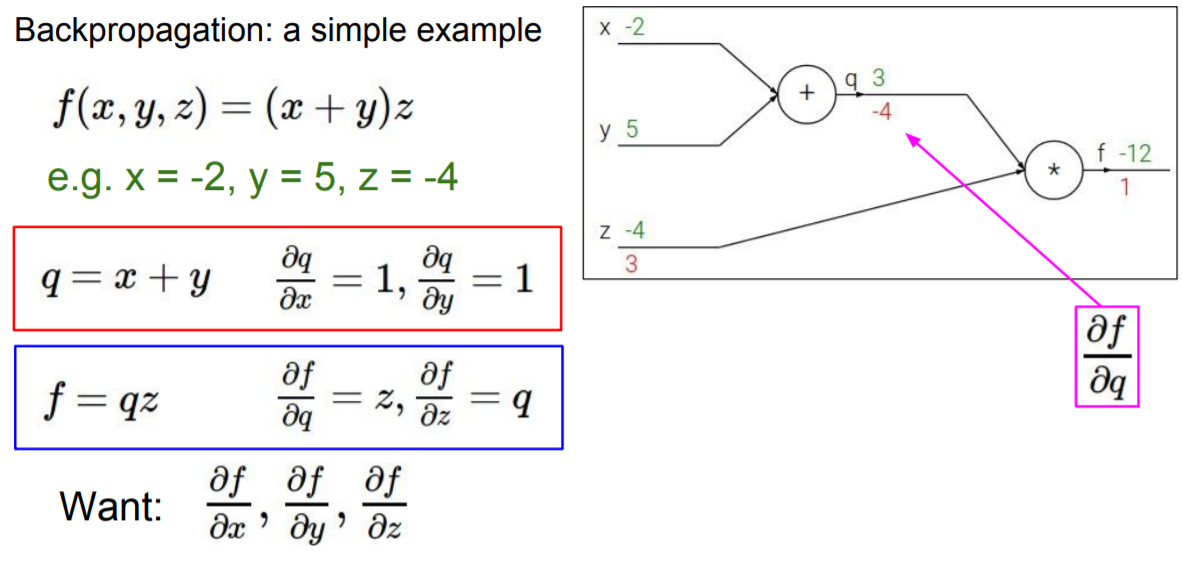
위의 그래프에서 볼 수 있듯이 $\frac{\partial f}{\partial f}$, $\frac{\partial f}{\partial z}$, $\frac{\partial f}{\partial q}$를 구하는 것은 어렵지 않다. 문제는 그 다음부터인데 그래프의 위쪽 nodes를 살펴보면 결국 parameter x에 대한 미분값이 필요한 데 $\frac{\partial f}{\partial y}$ 값을 한번에 구하기엔 그 사이에 다른 node가 들어 있어 불편하다는 것이다. 이때 사용할 수 있는 것이 바로 chain rule이다.

Chain rule

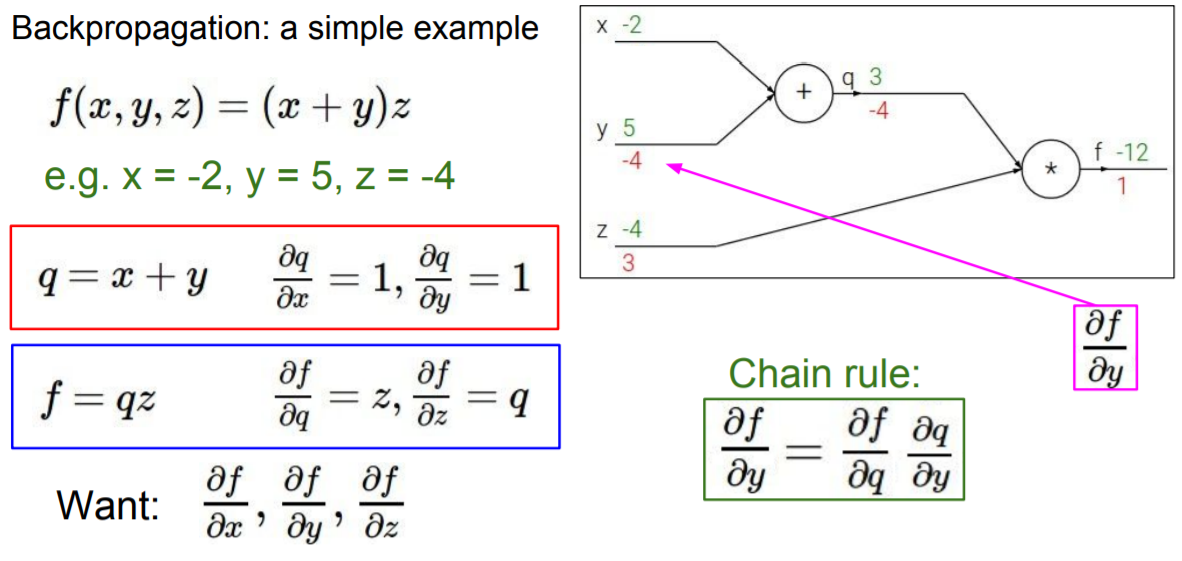
Chain rule이란 위의 식에서도 볼 수 있듯이 우리가 구할려고 하는 $\frac{\partial f}{\partial y}$를 $\frac{\partial f}{\partial q} \times \frac{\partial q}{\partial y}$ 로 분해해서 구할 수 있다는 내용을 말한다. 즉 한번에 $\frac{\partial f}{\partial y}$를 구할 필요없이 앞선 node에서 구했던 $\frac{\partial f}{\partial q}$에 $\frac{\partial q}{\partial y}$를 곱해서 $\frac{\partial f}{\partial y}$를 구할 수 있다는 것이다. 전체 함수인 $f$의 미분값은 global gradient라고 부르지만 $f$가 아닌 중간 nodes에 위치한 것의 미분값은 local gradient라고 부른다.

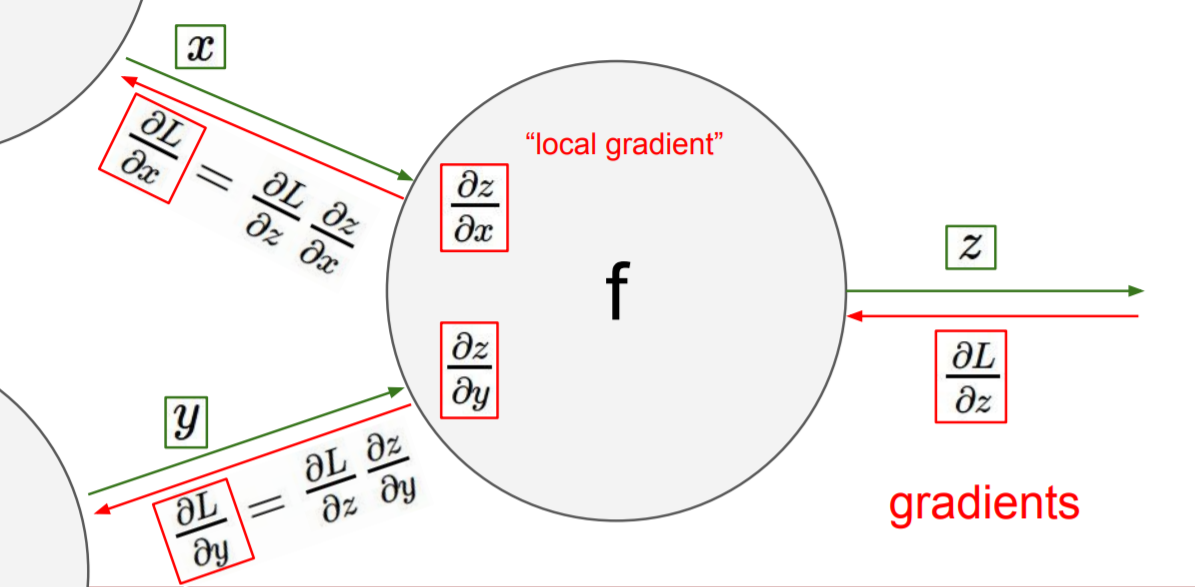
Forward pass 하는 과정에서 local gradient 를 구할 수 있다. 따라서 이를 메모리에 미리 저장해 두고 후에 backpropagation 을 진행할 때 global gradient를 구하고 chain rule을 이용해 하나씩 하나씩 각 node에 대한 미분값을 구하고 최종적으로는 parameters에 대한 미분값을 구해 update를 진행한다.

Module

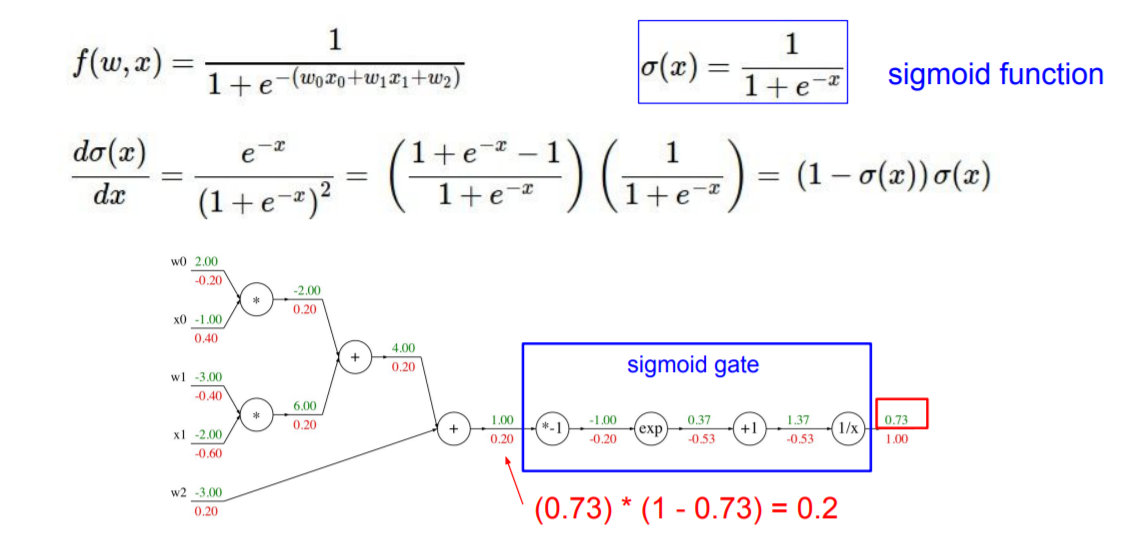
위의 그래프는 sigmoid function에 대해서 backpropagation을 진행한 다른 예제이다. 다만 sigmoid function은 직접 analytic gradient를 할 수 있기 때문에 위의 그래프에서 sigmoid gate를 하나로 묶어 직접 미분해서 구현하면 일일이 backpropagation을 하는 것보다 좀 더 빠르게 값을 구할 수 있다. 이렇게 직접 미분할 수 있는 함수들을 포함하고 있으면 이들을 모듈화해서 미분을 하는 것이 더 유용하다.

2. Neural Networks

앞서 배운 backpropagation은 Neural Networks를 학습시키는 데 매우 유용하다. Neural Networks란 deep learning에서 기본적으로 사용하는 틀로 생물학의 신경망에서 영감을 받아 만든 모델이다. 먼저 neural networks가 무엇인 지부터 살펴보려 한다.

1) Neural Networks란?

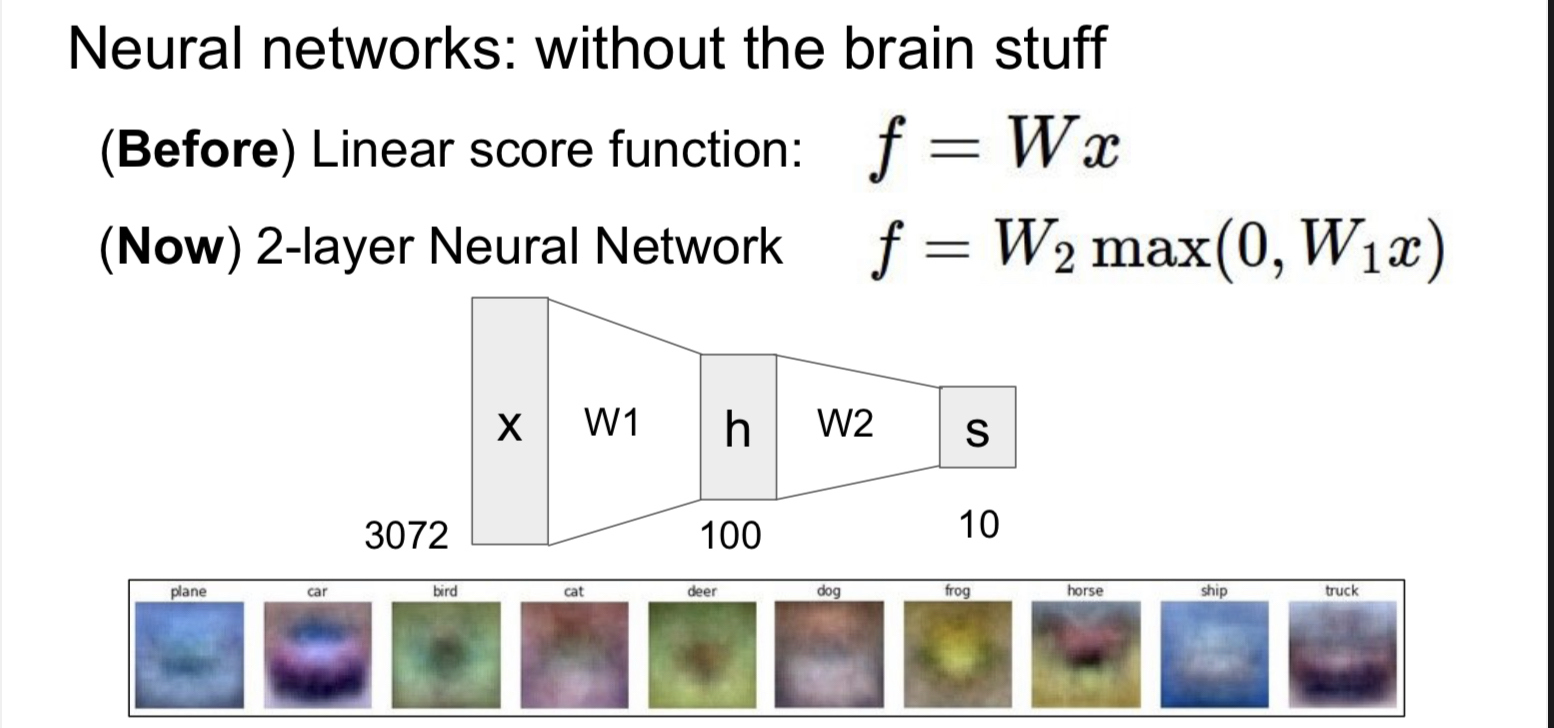
Neural network를 공부하기에 앞서 우리는 지난 시간이 linear function에 대해서 배웠다. 이 linear function을 non-linear한 다른 함수에 넣어 layer을 쌓는 방식이 바로 neural networks의 기본 구조이다. 레고 블록을 쌓듯이 층층이 layer를 쌓아 인공 신경망인 neural networks를 만드는 것이다. 그렇다면 왜 non-linear function이 필요한 것일까? 이는 neural network가 생물학적 신경망의 어떤 부분에서 아이디어를 얻었는 지를 살펴 보면 알 수 있다.

2) Activation Function

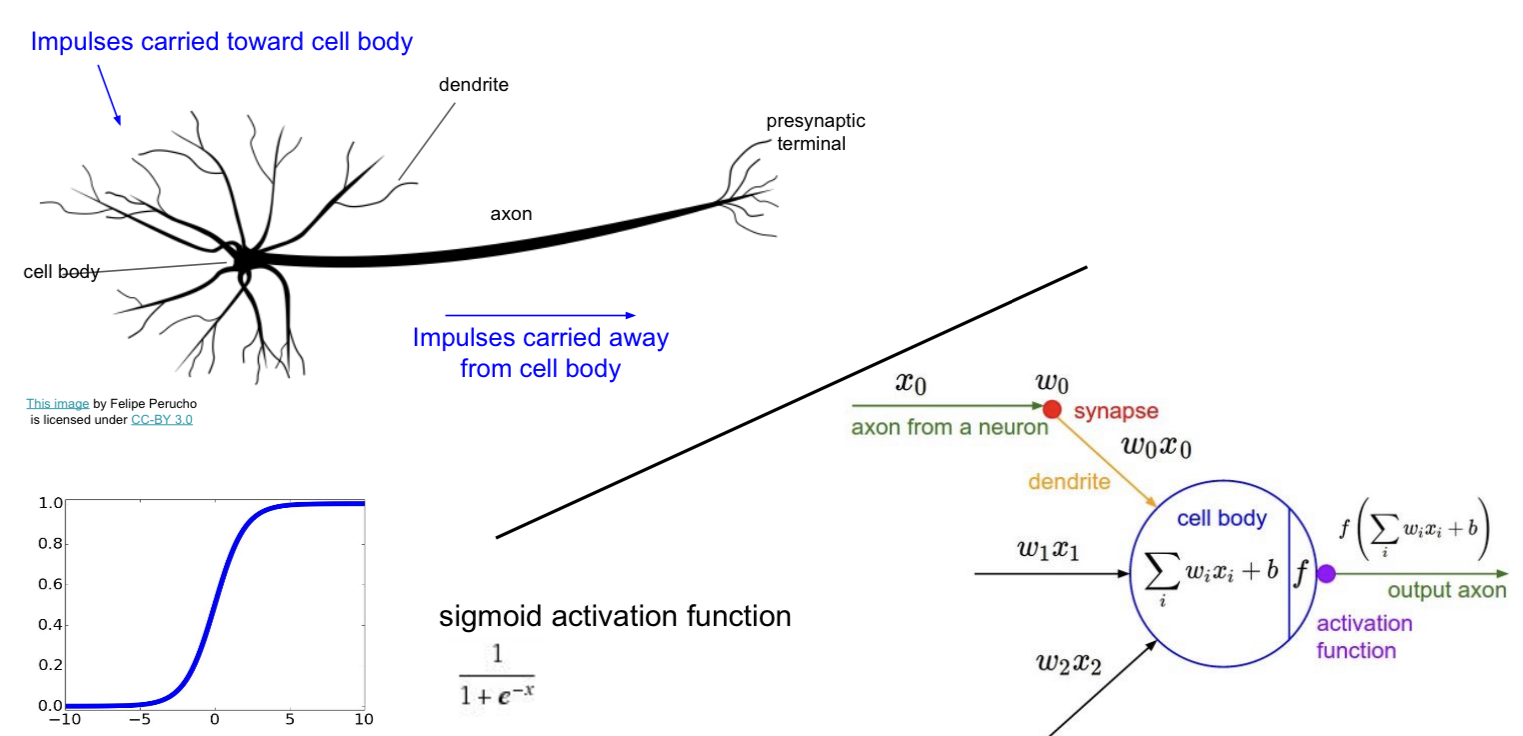
생물학적 뉴런은 앞선 뉴런으로부터 받은 신호가 특정 임계치를 넘으면 다음 뉴런으로 신호를 보내게 된다. 이 점에서 영감을 받아 만들어진 neural networks 역시 activation function을 이용해 활성인지 비활성인지를 표현한다.

요즘 기본적으로 많이 쓰이는 activation function은 ReLU라고 한다.

3) Architectures of Neural Networks

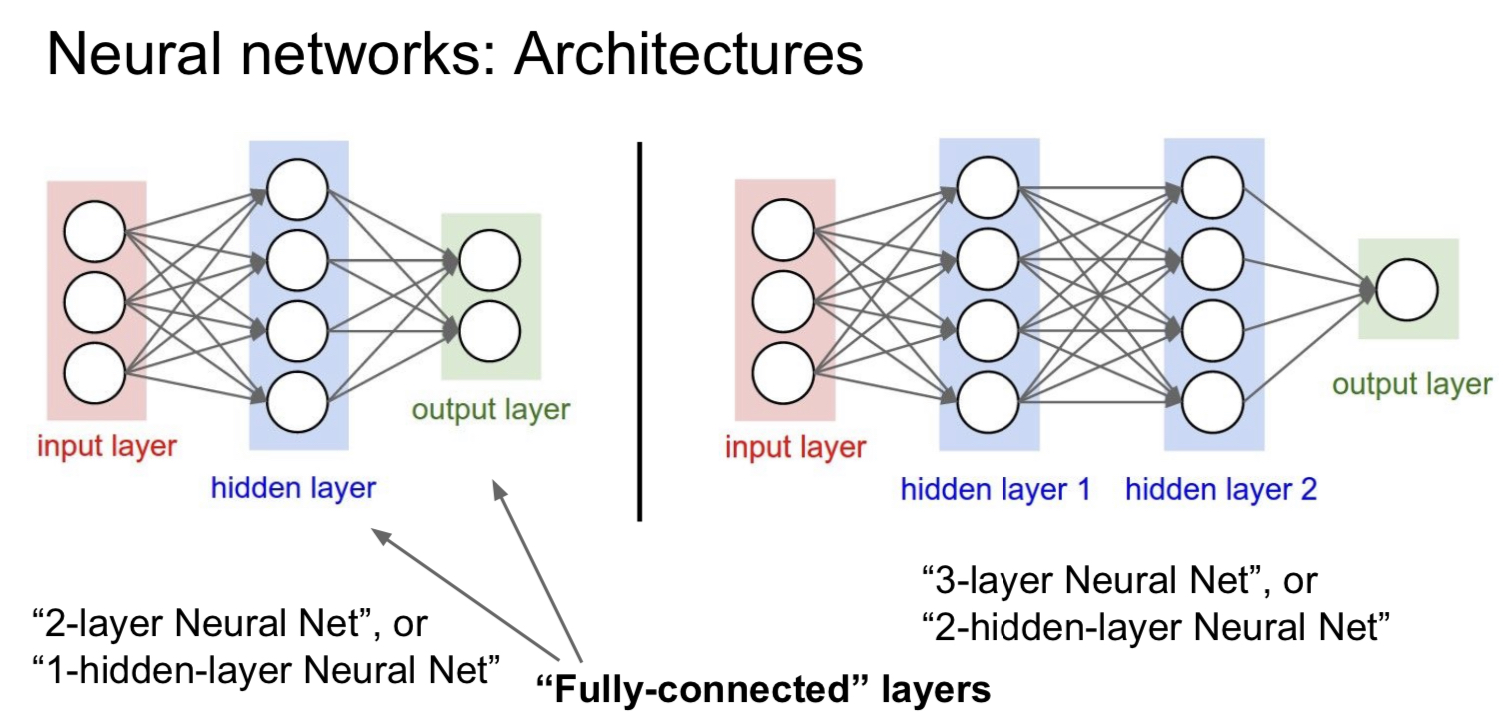
따라서 neural networks는 각 layer 별로 여러 nodes가 존재하고 이 nodes 들이 다음 layer의 또 다른 nodes에 연결 되어 있는 형태로 형성이 된다. 각 nodes들은 activation function으로 이루어져 있으며 이전 layer에서 들여온 값을 activation function에 넣어 값을 구하고 이 값을 다음 layer에 넘기는 방식이다.

참고자료

CS231n youtube 강의
CS231n 강의노트