Cross Entropy Loss

유승한·2024년 10월 21일

딥러닝

목록 보기

3/15

1. 엔트로피 (Entropy)란?

불확실성의 정도를 측정하는 척도입니다. 최적의 전략 하에서 그 사건을 예측하는데 필요한 질문개수에 대한 기댓값으로도 볼 수 있습니다.

어떤 확률 분포 p가 주어졌을 때, 그 분포의 엔트로피 H(p)는 다음과 같습니다.

H(p)=−∑^Cp_ilog(p_i)

C는 클래스의 수, $p_i$ 는 클래스 i에 속할 확률

엔트로피는 확률 분포가 얼마나 평평한지를 측정합니다. 모든 클래스가 동일한 확률을 가질 때 엔트로피는 최대가 되며, 특정 클래스의 확률이 커질수록 엔트로피는 감소합니다. 엔트로피가 감소한다는 것은 사건을 맞히기 위한 필요한 질문의 개수가 줄어드는 것을 의마하며 질문의 개수가 줄어든다는 사실은 정보량이 줄어든다는 의미입니다.

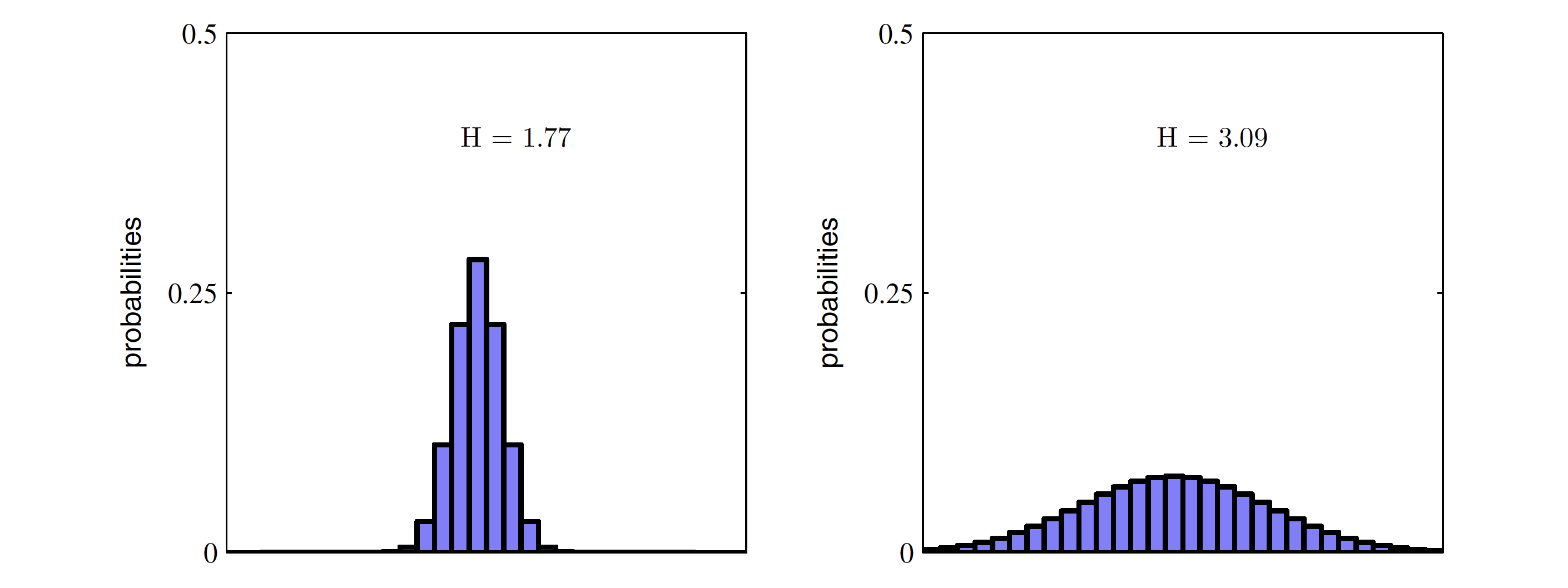
*Pattern Recognition and Machine Learning, C.M. Bishop*

Pattern Recognition and Machine Learning, C.M. Bishop

유도과정

$H=∑(사건발생확률)⋅log({1\over사건발생확률})=∑p_i log({1\over p_i})=−∑p_i log(p_i)$

2. 교차 엔트로피(Cross Entropy)

Cross Entropy는 두 확률 분포 p와 q간의 차이를 측정합니다. p가 주어졌을 때 q가 얼마나 잘 예측하는지를 나타냅니다.

H(p,q)=−∑^C{p_i}log(q_i)

이 식은 실제 분포 p와 예측된 분포 q간의 불일치를 측정합니다. p가 주어졌을 때 q가 얼마나 잘 예측하는지를 나타냅니다.

3. KL Divergence를 통한 Cross Entropy 도출

KL Divergence( $D_{kL}(p∥q)$ )는 두 확률분포 p와 q 간의 차이를 측정하는 또 다른 방법입니다. KL Divergence는 다음과 같습니다.

D_{KL}(p∥q)=∑^C{p_i}log({p_i\over q_i}) = H(p,q) - H(p)

KL Divergence는 두 분포가 동일할 때 0이 되며, 차이가 클수록 값이 커지며 위와과 같이 Cross Entropy와 연결될 수 있습니다.

4. Cross Entropy Loss 도출

모델의 손실 함수로 사용되는 Cross Entropy Loss는 실제 레이블이 원-핫 인코딩으로 표현된다고 가정합니다. 이 경우, 실제 분포 p는 한 클래스에서만 1이고 나머지 클래스에서는 0인 벡터입니다.

따라서 Cross Entropy는 다음과 같이 단순화됩니다.

Cross Entropy Loss=−∑^C{p_i}log(q_y)

여기서 실제 pi는 원-핫 벡터이므로, 실제로 $p_i = 1$ 인 위치에서만 값이 남고 나머지는 사라집니다. 즉, Cross Entropy Loss는 모델이 예측한 $q_i$ 중에서 실제 레이블에 해당하는 위치의 $q_i$ 에 대한 로그 확률만을 계산하는 형태로 나타냅니다.

Cross Entropy Loss=−log(q_y)

여기서 y는 실제 레이블에 해당하는 클래스입니다.

5. Binary Cross Entropy Loss 도출

이제 이 개념을 이진 분류(Binary Classification) 문제에 적용해봅시다. 이 경우, C = 2이고, 실제 레이블 y는 0 또는 1이 될 수 있습니다. 모델이 예측한 확률을 p라고 할 때, 이진 교차 엔트로피 손실(Binary Cross Entropy Loss)은 다음과 같이 도출됩니다

Binary Cross Entropy Loss=−[ylog(p)+(1−y)log(1−p)]

여기서:

y는 실제 레이블 (0 또는 1).
p는 모델이 예측한 양성 클래스에 대한 확률입니다.

이 손실 함수는 y=1일 때는 −log⁡(p)를 최소화하고, y=0일 때는 −log⁡(1−p)를 최소화하도록 모델을 학습시킵니다.

6. Cross Entropy Loss의 직관적 의미

모델 학습: Cross Entropy Loss는 모델이 실제 레이블에 대한 예측 확률을 높이도록 최적화합니다. 예측 확률 $p_i$ 가 실제 레이블에 가까워질수록 손실이 줄어들고, 모델이 잘못된 예측을 할수록 손실이 커집니다.
확률 해석: 이 손실 함수는 확률 분포 간의 차이를 측정하므로, 모델의 예측을 확률적으로 해석할 수 있게 합니다.