KL-divergence

유승한·2024년 10월 21일

딥러닝

목록 보기

4/15

0. Kullback-Leibler Divergence란?

Kullback-Leibler Divergence (KL Divergence)는 두 확률 분포 간의 차이를 측정하는 비대칭적인 척도입니다. 주로, 한 확률 분포가 다른 확률 분포와 얼마나 다른지 또는 얼마나 멀리 떨어져 있는지를 계산할 때 사용됩니다. 정보 이론에서 KL Divergence는 두 분포 간의 "상대 엔트로피"라고도 불립니다.

위키피디아 설명

쿨백-라이블러 발산(Kullback–Leibler divergence, KLD)은 두 확률분포의 차이를 계산하는 데에 사용하는 함수로, 어떤 이상적인 분포에 대해, 그 분포를 근사하는 다른 분포를 사용해 샘플링을 한다면 발생할 수 있는 정보 엔트로피 차이를 계산한다. 상대 엔트로피(relative entropy), 정보 획득량(information gain), 인포메이션 다이버전스(information divergence)라고도 한다.

1. 정의

KL Divergence는 두 확률 분포 P와 Q가 있을 때, 분포 P가 Q와 얼마나 다른지 나타내는 값을 계산합니다. KL Divergence의 수식은 다음과 같이 정의됩니다:

$D_{KL}(P∥Q)=∑_xP(x)log{⁡P(x)\over Q(x)}$

또는, 연속적인 확률 분포의 경우:

$D_{KL}(P∥Q)=∫P(x)log{⁡P(x)\over Q(x)}dx$

여기서:

P(x)는 실제 분포 또는 참조하는 분포입니다.
Q(x)는 근사하거나 비교하려는 분포입니다.
x는 확률 변수입니다.

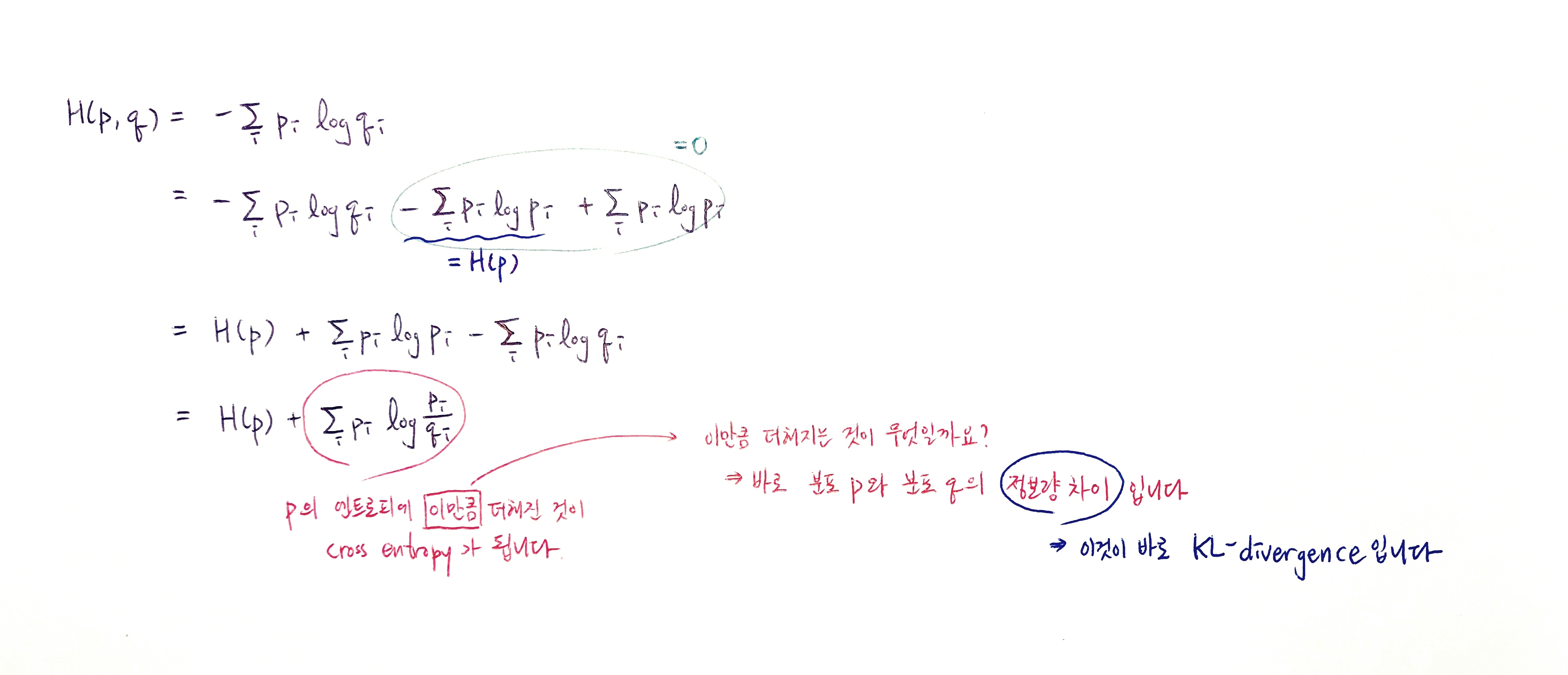
출처 : https://hyunw.kim/blog/2017/10/27/KL_divergence.html

Cross Entropy를 통해 위의 수식과 같이 KL을 도출해낼 수 있습니다.

$KL(p∥q)=H(p,q)−H(p)$

따라서 cross entropy를 최소화하는 것은, H(p)가 고정된 상수값이기에 KL Divergence를 최소화하는 것과 같습니다.

2. KL-divergence의 특성

$KL(p|q)≥0$

$H(p,q)≥H(p)$ 이므로 $H(p,q)−H(p)≥0$ 이 도출됩니다. $H(p,q)≥H(p)$ 인 이유는 cross entropy의 lower bound가 entropy이기 때문입니다.

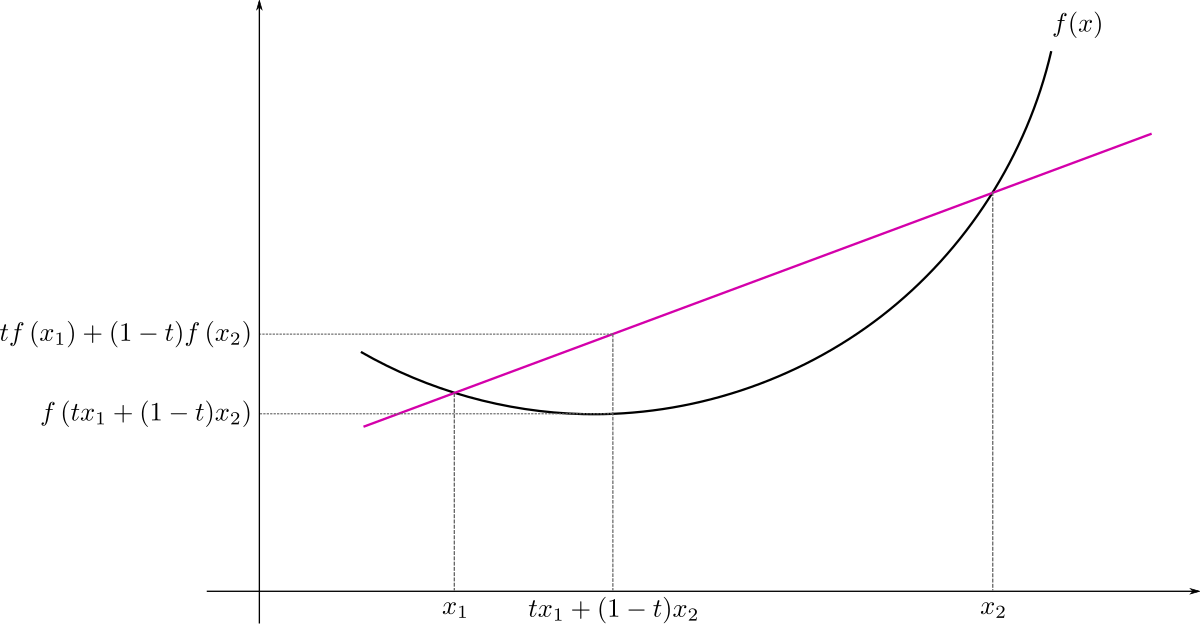
convex function, wikipidia

이 부등식을 사용하려면 우선 convex function, 소위 말하는 아래로 볼록한 함수를 엄밀하게 정의해보겠습니다. 위 그림을 위키피디아에서 가져와봤습니다. 두 점 x1,x2x1,x2와 그 사이에 있는 점 tx1+(1−t)x2tx1+(1−t)x2을 생각해보겠습니다( $t∈ [0,1]$ ). 가운데 점의 식은 두 점 $x_1,x_2$ 의 weighted sum입니다. 그리고 이제 그 가운데 점을 함수 $f(x)$ 에 넣었을 때 나온 값 $f(tx_1+(1−t)x_2)f(tx_1+(1−t)x_2)$ 와 두 점 $x_1,x_2$ 를 각각 $f(x)$ 에 넣은 값의 weighted sum인 $t(f(x_1))+(1−t)f(x_2)$ 을 비교합니다. Convex function이라면 이 두 가지 값을 크기 비교했을 때 언제나 이런 결과가 나옵니다.

$f(tx_1+(1−t)x_2)≤t(f(x_1))+(1−t)f(x_2)$

이를 확률론의 맥락에서는 X가 random variable이고, f(⋅)f(⋅)가 convex function일 때, 이렇게 표현합니다.

$f(E[X])≤E[f(X)]$

이제 준비운동을 다 마쳤으니 KL-divergence에 관련해서 증명을 해보겠습니다. 우리의 KL-divergence 식에 있는 $−log$ 를 $f(x)$ 로 두고 가운데의 weighted sum 또는 $E[X]$ 를 $q_i\over p_i$ 로 두면 Jensen’s 부등식에 넣을 수 있습니다.

$KL(p∥q)=−∫p(x)log{q(x) \over p(x)}dx≥−log∫p(x){q(x)\over p(x)}dx =−log∫q(x)dx=−log1=0$

$∴KL(p∥q)≥0$

따라서 KL-divergence은 non-negative의 특성을 가집니다.