1. Manifold Learning이란?
manifold learning이란 고차원 데이터를 저차원에 매핑하는 비선형 차원 축소 기법입니다. 이는 데이터의 복잡성을 낮추고 중요한 패턴을 발견하는데 유용합니다.
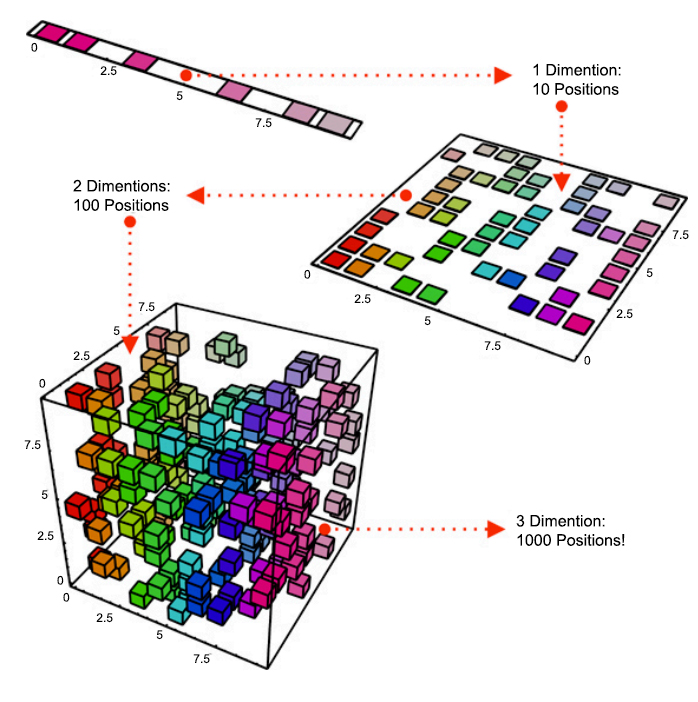

직관적으로 알아봅시다. 위 사진은 이활석 교수님의 오토인코더의 모든 것 강의에서 발췌했습니다. d를 2차원으로 가정하고 m을 3차원으로 가정할 시에, manifold는 3차원에 분포된 훈련 데이터들을 표현할 수 있는 subspace를 의미합니다. 이러한 subspace를 2차원 공간으로 프로젝션 함으로써 데이터 차원을 축소하는 것이 manifold learning이라고 할 수 있습니다.
2. Manifold Learning이 사용될 때
-
데이터 압축
jpeg 보다 압축 후 복원할 시에 복원 정도가 상당히 높음
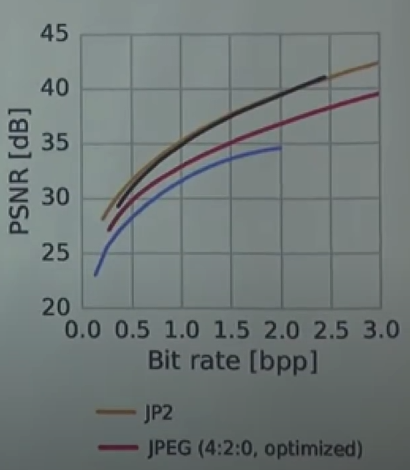
-
데이터 시각화
t-SNE
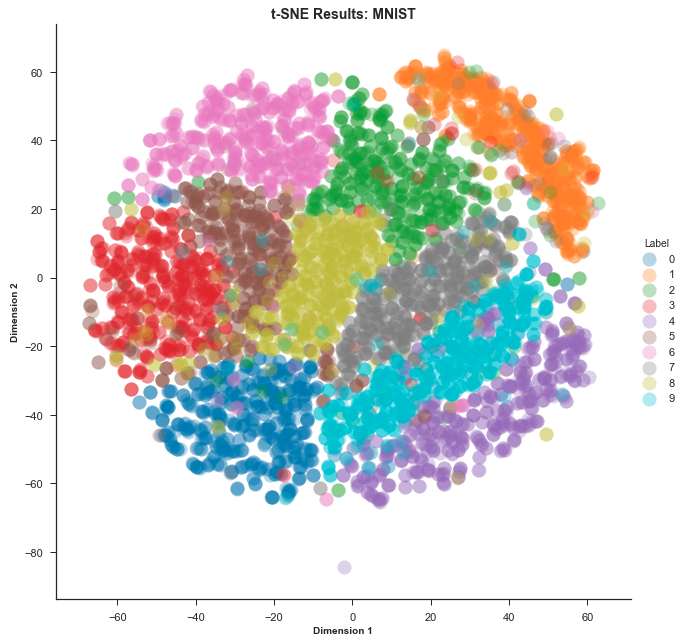
-
차원의 저주(Curse of dimensionality)
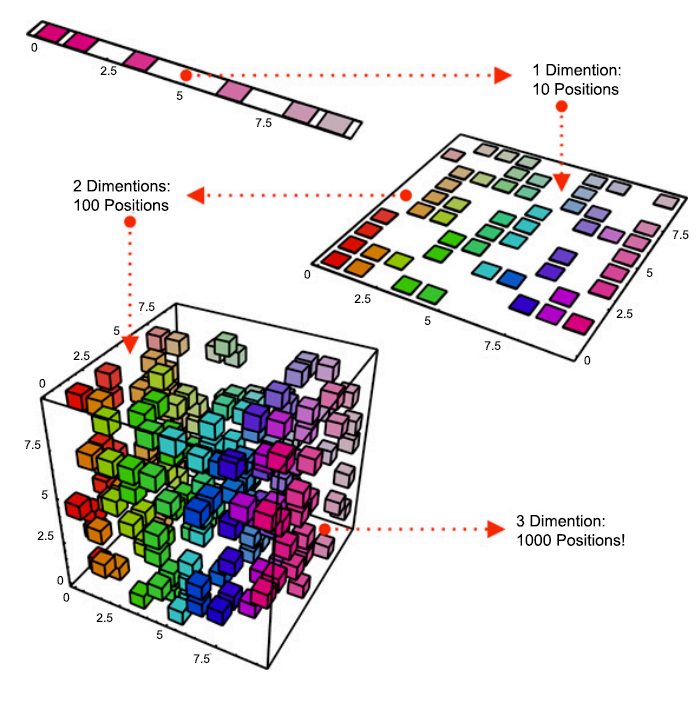
같은 데이터 샘플에서 차원이 증가할수록 밀도가 희박해집니다. 밀도가 희박해짐으로써 데이터의 분포 분석 또는 모델 추정에 필요한 샘플 데이터 개수가 기하급수적으로 증가하게 됩니다.
-
가장 중요한 특징(feature) 도출
3. Manifold의 가정

위 가정을 통해 고차원의 데이터 밀도는 낮지만, 고차원 데이터를 표현하는 저차원의 Manifold는 밀도가 높으며, 데이터의 샘플 데이터의 특징을 표현하고 있음을 알 수 있습니다. 따라서 특정 데이터 포인터와 비슷한 종류의 데이터를 매니폴드 상 근처에 있는 데이터들에게 기대할 수 있습니다.
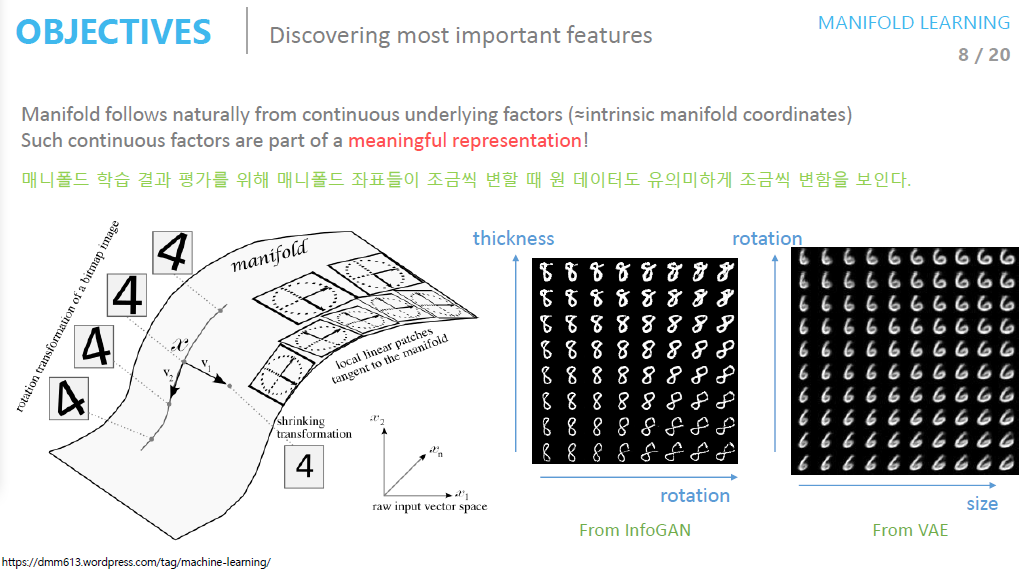
앞서서 설명한 대로 고차원의 데이터를 잘표현한 매니폴드는 곧 중요한 특징을 발견할 수 있게됩니다. 위의 예시에서는 세로축이 곧 방향이 되고 가로축은 두께라는 특징을 가지고 있음을 알 수 있습니다.
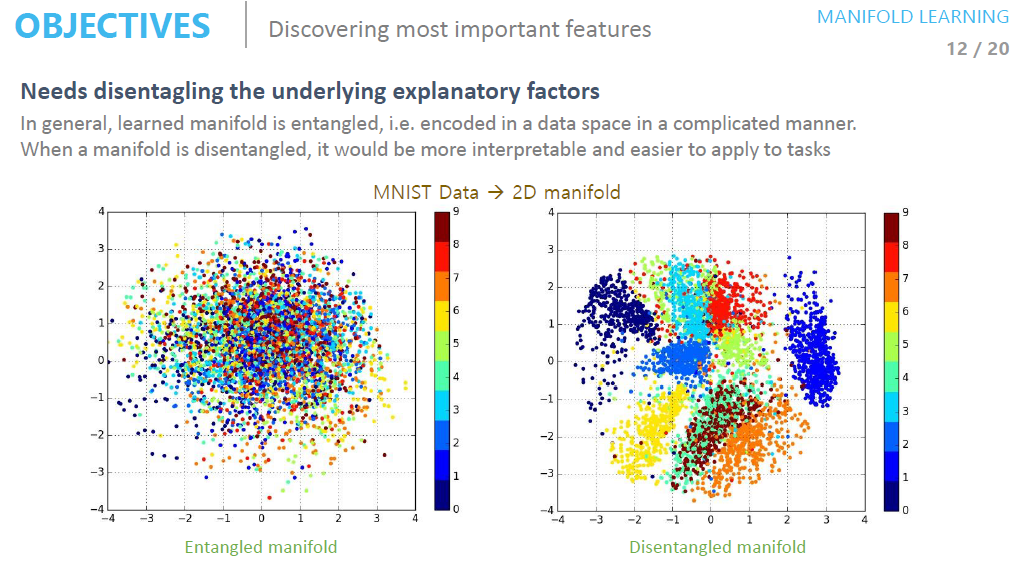
이렇듯 학습이 잘된 manifold는 주요 특징을 찾아내 전보다 명확히 분류됨을 알 수 있습니다.
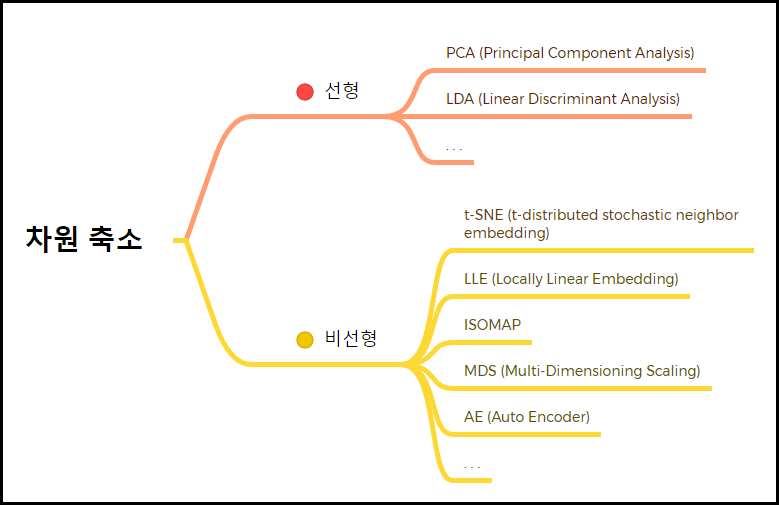
4. 그 외 차원축소기법
Reference
https://www.youtube.com/watch?v=o_peo6U7IRM&list=PLsFtzQAC8dDetav3jSCKB_MXwvUn7yfJS&t=1863s
