1. 오토인코더란?
입력 데이터를 주요 특징으로 효율적으로 압축(인코딩)한 후 이 압축된 표현에서 원본 입력을 재구성(디코딩)하도록 설계된 일종의 신경망 아키텍처입니다.
IBM 발췌
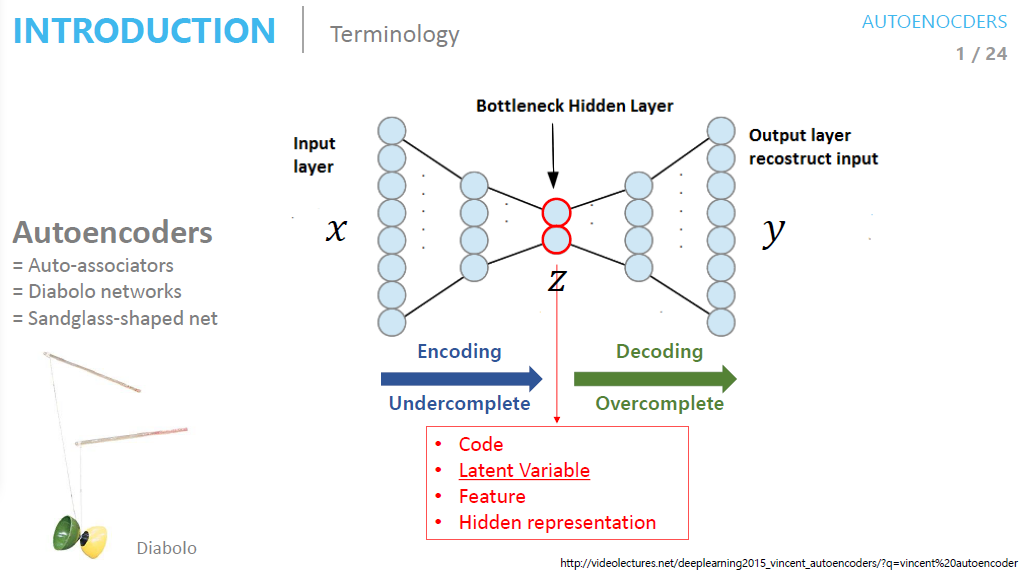
Autoencoder는 다양한 이름으로 불립니다.
- Auto-associators : 입출력에 자기 관계가 있다
- Diabolo networks, Sandglass-shaped net : diabolo와 sandglass 모양과 비슷하다
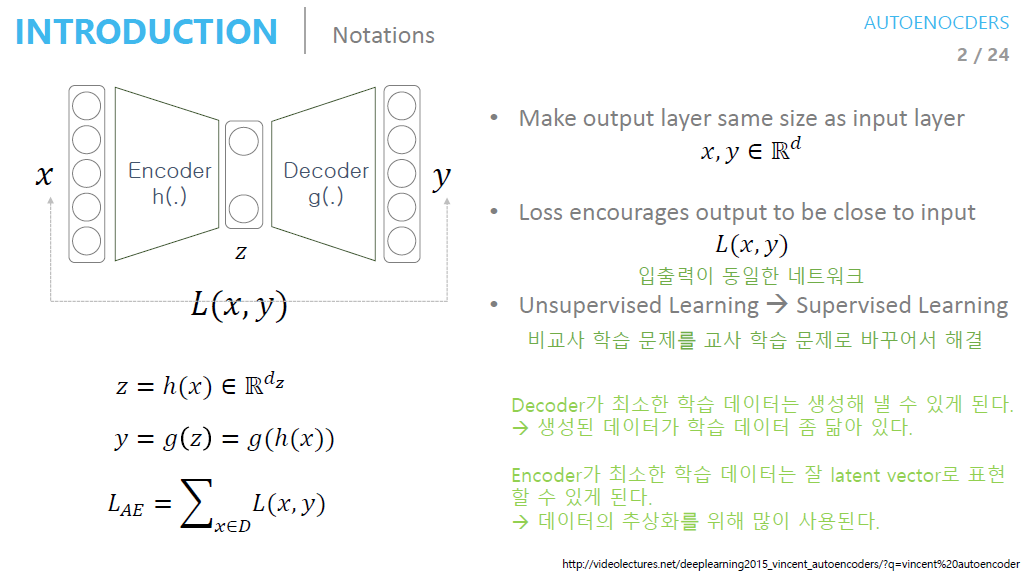
입력 레이어와 출력 레이어가 같은 크기입니다
손실함수 L(x,y)
- 입출력이 동일한 네트워크입니다
- 예를 들어 차원 축소 알고리즘의 정답을 매길 수 없기에 unsupervised로 진행해야하지만 autoencoder를 통해 self learning 등을 통해 supervised learning을 수행할 수 있습니다
Encoder가 최소한 학습 데이터는 latent vector로 잘 표현 할 수 있게 됩니다
- 데이터의 추상화를 위해 많이 사용됩니다
Decoder가 최소한 학습 데이터는 생성해낼 수 있게 됩니다.
- 생성된 데이터가 학습 데이터를 닮아 있기 때문입니다
p.s. GANs와 달리 autoencoder는 이러한 특성 덕에 최소한의 성능을 보장합니다
p.p.s autoencoder의 목적은 manifold learning에 있습니다.
2. Stacked autoencoder
Stacked Autoencoder(SAE)는 여러 개의 Autoencoder를 층(layer)으로 쌓아올려 심층 신경망을 형성한 구조입니다. Autoencoder는 입력 데이터를 압축(encoding)하고, 다시 이를 복원(decoding)하는 과정을 학습하는 비지도 학습 방식의 신경망입니다. Stacked Autoencoder는 이러한 Autoencoder를 여러 층으로 쌓아 더 복잡한 데이터 구조를 학습할 수 있게 하는 방법입니다.
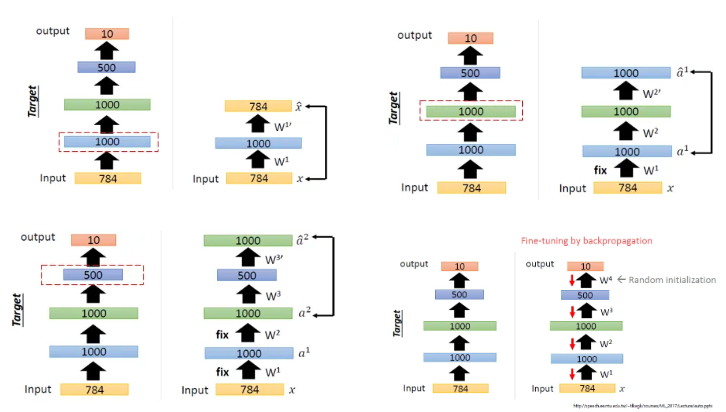
autoencoder의 input data에 대해서 복원을 잘하는 특징을 이용해 모델의 가중치를 초기화하는데 사용되었습니다. 초기화된 모델은 역전파를 이용해 학습을 진행하게 됩니다.
3. Denoising autoencoder
Denoising Autoencoder(DAE)는 Autoencoder의 변형 중 하나로, 입력 데이터에 노이즈를 추가하여 그 데이터를 복원하도록 학습시키는 신경망 구조입니다. Denoising Autoencoder의 핵심 아이디어는 데이터에 일부 손상이 있더라도 원본 데이터를 정확히 복원하는 능력을 신경망이 학습하도록 하는 것입니다. 이는 일반적인 Autoencoder보다 더 강력한 표현 능력을 가지며, 노이즈 제거, 특징 학습, 차원 축소 등 다양한 응용에서 사용됩니다.
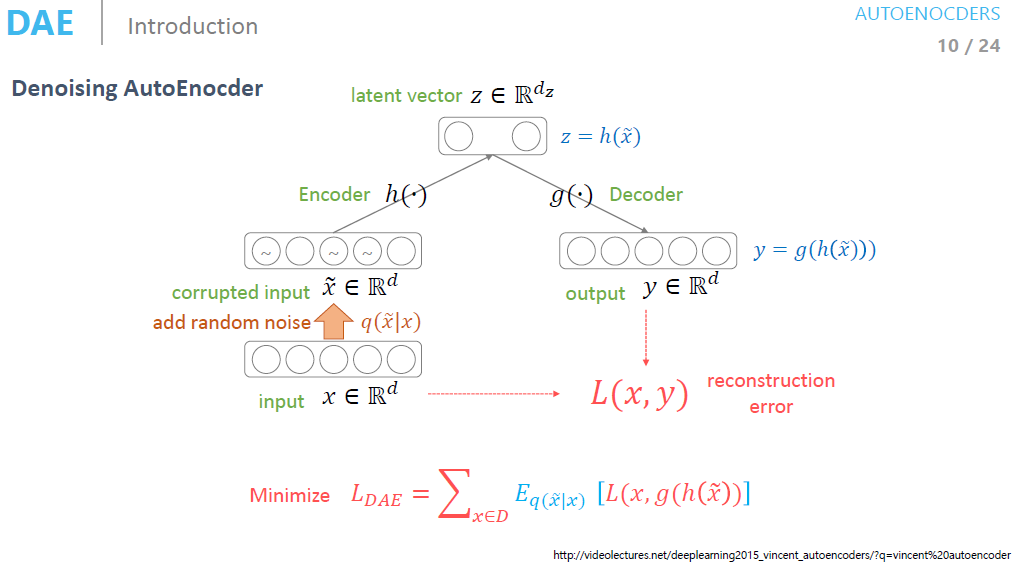
쉬운 예시를 들어보겠습니다. 특정 사진, 음성에 노이즈가 발생한다 하여도 사람의 인식 상으로는 사진과 음성을 특정하는 데에는 크게 무리가 없을 수 있습니다. 해당 예시와 denosing autoencoder의 원리는 동일합니다. autoencoder에서 일정 수준의 노이즈가 추가된 입력 데이터라고 하더라도 manifold는 상에서의 분포에는 변화가 없다는 가정 하에 원본데이터를 정확히 복원하게끔 학습됩니다.

denoising autoencoder가 autoencoder과 비교하여 filter가 edge 추출이 잘됨을 볼 수 있습니다. 이는 곧 학습이 잘되었고 성능이 뛰어남을 의미합니다.
4. Stacked Denoising Autoencoder(SDAE)
Stacked Denoising Autoencoder (SDAE)는 여러 개의 Denoising Autoencoder를 계층적으로 쌓아 구성된 심층 신경망입니다. 이는 원본 데이터에 노이즈를 추가하고, 이 노이즈를 제거하여 원본 데이터를 복원하는 과정을 학습하는 Denoising Autoencoder를 여러 층으로 연결한 심층 구조로, 복잡한 데이터의 특징을 학습하고 표현하는 데 유용합니다.
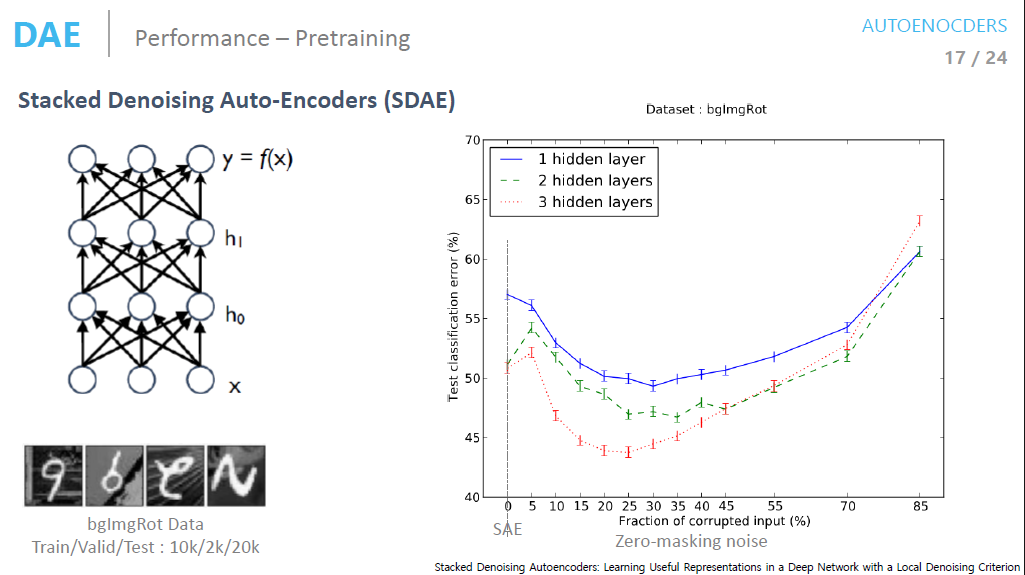
zero-masking noise 정도에 따른 error 정도를 분석할 시에 특정 noise 정도까지는 에러율이 개선됨을 알 수 있지만 그 이상으로 노이즈가 많아질 시에 에러율이 높아짐을 알 수 있습니다. 노이즈가 과도하게 많아질 시에 기존 데이터의 특성을 잃게 되기 때문입니다.
Reference
https://www.youtube.com/watch?v=rNh2CrTFpm4&list=PLsFtzQAC8dDetav3jSCKB_MXwvUn7yfJS&index=8
