강화학습 기초 2

김민수·2024년 12월 25일

reinforce learing 강화학습 수업자료

수업자료_강화학습

목록 보기

2/3

강화학습 개념 및 Markov Decision Process (MDP) 이해

1. 강화학습의 주요 구성 요소

강화학습은 에이전트가 환경과 상호작용하며 최적의 행동을 학습하는 방식입니다. 이 과정에서 중요한 구성 요소들이 있습니다: 에이전트, 환경, 상태, 행동, 보상입니다.

1.1 에이전트 (Agent)

에이전트는 강화학습의 주체로, 환경과 상호작용하며 행동을 취하고 보상을 받습니다. 에이전트는 주어진 목표를 달성하기 위해 정책(policy)을 학습하고, 이를 통해 최적의 행동을 선택합니다.

에이전트의 역할: 주어진 환경에서의 최적의 행동을 학습하는 주체
에이전트의 목표: 보상을 최대화하는 행동을 찾아내는 것

1.2 환경 (Environment)

환경은 에이전트가 상호작용하는 외부 세계입니다. 에이전트의 행동에 반응하여 상태를 변화시키고, 보상을 제공합니다. 환경은 에이전트가 받는 피드백의 출처이며, 에이전트는 이 환경에 의해 행동 결과를 인식합니다.

환경의 역할: 에이전트의 행동에 따라 상태를 변화시키고 보상을 제공
환경의 목표: 에이전트가 최적의 행동을 학습하도록 돕는 것

1.3 상태 (State)

상태는 환경의 특정 순간을 나타내며, 에이전트가 어떤 행동을 취할지 결정하는 중요한 정보입니다. 환경은 여러 개의 상태로 구성되며, 에이전트는 현재 상태를 기반으로 행동을 선택합니다.

상태의 정의: 환경의 특정 시점에서의 정보나 조건
상태의 예: 체스에서의 보드 상태, 로봇의 위치와 속도

1.4 행동 (Action)

행동은 에이전트가 선택하는 결정으로, 환경에 영향을 미칩니다. 에이전트는 다양한 가능한 행동 중 하나를 선택하고, 그 행동이 결과적으로 상태를 변화시키고 보상을 초래합니다.

행동의 정의: 에이전트가 선택할 수 있는 행동들
행동의 예: 체스에서의 기물 이동, 로봇의 회전

1.5 보상 (Reward)

보상은 에이전트가 행동을 통해 얻는 피드백입니다. 에이전트는 보상을 최대화하려는 목표를 가지고 학습합니다. 보상은 긍정적일 수도, 부정적일 수도 있으며, 장기적으로 보상을 극대화하는 행동을 학습하는 것이 목표입니다.

보상의 정의: 에이전트가 행동을 통해 받는 피드백
보상의 예: 체스에서 상대의 기물을 잡았을 때 얻는 점수, 로봇이 목표 지점에 도달했을 때 받는 보상

2. Markov Decision Process (MDP)

Markov Decision Process(MDP)는 강화학습 문제를 모델링하는 수학적 틀입니다. MDP는 에이전트가 환경과 상호작용하며 최적의 정책을 학습하는 과정을 정의합니다. MDP는 네 가지 주요 구성 요소로 이루어져 있습니다:

상태(State, S): 환경의 특정 시점에서의 상태
행동(Action, A): 에이전트가 선택할 수 있는 행동
전이 확률(Transition Probability, P): 에이전트가 특정 상태에서 행동을 선택했을 때, 다음 상태로 전이될 확률
보상 함수(Reward Function, R): 에이전트가 특정 상태에서 행동을 취할 때 받는 보상

2.1 Markov Property

MDP는 Markov Property를 따릅니다. 이는 "현재 상태는 이전 상태들과 상관없이 다음 상태를 결정하는 데 충분하다"는 성질입니다. 즉, 에이전트가 현재 상태에서 어떤 행동을 선택하면, 그 결과로 다음 상태와 보상이 결정됩니다. 과거의 상태나 행동은 현재 상태와 보상에 영향을 미치지 않습니다.

2.2 MDP의 수학적 정의

MDP는 5개의 주요 요소로 정의됩니다:

S: 상태 공간 (가능한 모든 상태들의 집합)
A: 행동 공간 (가능한 모든 행동들의 집합)
P(s'|s, a): 전이 확률 함수 (현재 상태 s에서 행동 a를 취했을 때, 상태 s'로 전이될 확률)
R(s, a): 보상 함수 (현재 상태 s에서 행동 a를 취했을 때 얻는 보상)
γ (Gamma): 할인 인자 (미래의 보상에 대한 현재 가치 평가)

2.3 최적 정책(Optimal Policy)

MDP에서 최적의 정책은 에이전트가 각 상태에서 어떤 행동을 선택해야 하는지를 결정합니다. 이를 통해 에이전트는 장기적으로 보상을 최대화할 수 있습니다. 최적 정책을 찾는 과정은 벨만 방정식을 통해 해결됩니다.

2.4 Bellman 방정식

벨만 방정식은 상태에서 최적 행동을 선택하는 수학적 방법을 제공합니다. 이 방정식은 각 상태에서 최적의 보상 값을 계산하는 데 사용됩니다. 최적 정책을 찾는 것은 이 방정식을 풀어 최적의 값을 찾아내는 과정입니다.

2.4.1 벨만 방정식의 기본 형태

벨만 방정식은 강화학습에서 가치 함수를 계산하고, 최적의 정책(Optimal Policy)을 찾는 데 중요한 역할을 합니다. 이 방정식은 벨만 기대방정식 (Bellman Expectation Equation)과 벨만 최적방정식 (Bellman Optimality Equation) 두 가지로 나뉩니다.

2.4.2 벨만 기대방정식 (Bellman Expectation Equation)

벨만 기대방정식은 주어진 정책 $\pi$ 에 대해 각 상태에서의 가치 함수를 계산하는 식입니다. 특정 정책 $\pi$ 에 대해 상태 (s)의 가치 $V^\pi$ 는 다음과 같이 정의됩니다:

$V^\pi(s) = \mathbb{E}_{\pi} \left[ R(s, a) + \gamma V^\pi(s') \right]$

여기서:
- $V^\pi(s)$ : 정책 $\pi$에 따른 상태 (s)의 가치 함수
- $R(s, a)$ : 상태 $s$ 에서 행동 $a$ 를 취했을 때 얻는 보상
- $\gamma$ : 할인 인자 (0과 1 사이의 값)
- $s'$ : 다음 상태
- $\mathbb{E}_{\pi}$ : 정책 $\pi$ 에 따른 기대값
이 방정식은 상태 $(s$ )에서 특정 정책 $\pi$ 를 따를 때, 상태 $(s$ )의 가치가 현재 보상과 미래 상태의 기대 가치의 합으로 구성된다는 것을 나타냅니다.

2.4.3 벨만 최적방정식 (Bellman Optimality Equation)

벨만 최적방정식은 최적 정책을 구하는 데 사용되는 방정식입니다. 상태 (s)에서의 최적 가치 함수 $(V^*(s)$ )는 다음과 같이 정의됩니다:

$V^*(s) = \max_a \left[ R(s, a) + \gamma \sum_{s'} P(s'|s, a) V^*(s') \right]$

여기서:
- $V^*(s)$ : 상태 $s$ 에서의 최적 가치 함수
- $R(s, a)$ : 상태 $s$ 에서 행동 $a$ 를 취했을 때 얻는 보상
- $\gamma$ : 할인 인자(감가율)
- $P(s'|s, a)$ : 상태 $s$ 에서 행동 $a$ 를 취했을 때, 상태 $s'$ 로 전이될 확률
이 방정식은 상태 (s)에서 가능한 모든 행동 중 가장 높은 보상을 제공하는 행동을 선택할 때의 가치를 계산합니다. 즉, 최적 가치 함수는 현재 보상과 미래 상태의 가치를 결합한 값 중 최댓값을 취하게 됩니다.

2.4.4 최적 정책 (Optimal Policy)

최적 정책 $(\pi^*(s)$ )는 주어진 상태 (s)에서 최적의 행동 $(a^*$ )를 선택하는 정책으로, 벨만 최적방정식을 사용하여 계산할 수 있습니다. 최적 정책은 다음과 같이 정의됩니다:

$\pi^*(s) = \arg\max_a \left[ R(s, a) + \gamma \sum_{s'} P(s'|s, a) V^*(s') \right]$

여기서:
- $\pi^*(s)$ : 상태 (s)에서 최적의 행동을 선택하는 정책
- $\arg\max$ : 가능한 행동 중 가장 큰 값을 주는 행동을 선택
2.4.5 벨만 방정식의 활용
- 벨만 방정식은 가치 반복(Value Iteration) 및 정책 반복(Policy Iteration) 알고리즘에서 중요한 역할을 하며, 이를 통해 에이전트는 최적 정책을 학습하고, 주어진 환경에서 장기적인 보상을 최대화할 수 있습니다.

3. 결론

에이전트, 환경, 상태, 행동, 보상은 강화학습에서 중요한 구성 요소입니다. 에이전트는 환경과 상호작용하며, 상태를 고려하여 행동을 선택하고 보상을 받습니다.
Markov Decision Process(MDP)는 강화학습 문제를 모델링하는 수학적 틀로, 상태, 행동, 전이 확률, 보상 함수 등의 요소를 통해 최적의 정책을 학습할 수 있게 합니다.
Markov Property를 따르는 MDP에서는 현재 상태만이 다음 상태를 결정하는 데 필요한 모든 정보를 제공하므로, 이전 상태는 필요하지 않습니다. 이를 통해 에이전트는 장기적인 보상을 최대화하는 최적의 정책을 학습할 수 있습니다.

1. OpenAI Gym

OpenAI Gym은 강화학습 환경을 제공하는 라이브러리로, 다양한 시뮬레이션 환경을 구축하여 강화학습 실험을 쉽게 할 수 있게 돕습니다. Gym은 강화학습을 위한 여러 환경을 제공하고, 이 환경들에서 에이전트를 훈련시킬 수 있습니다.

주요 특징:

다양한 환경(게임, 로봇 시뮬레이션, 제어 문제 등)을 제공합니다.
Python에서 쉽게 사용할 수 있으며, 강화학습 실험을 위한 표준화된 API를 제공합니다.
강화학습 알고리즘을 실험하는 데 필요한 모든 도구를 제공합니다.

환경 예시:

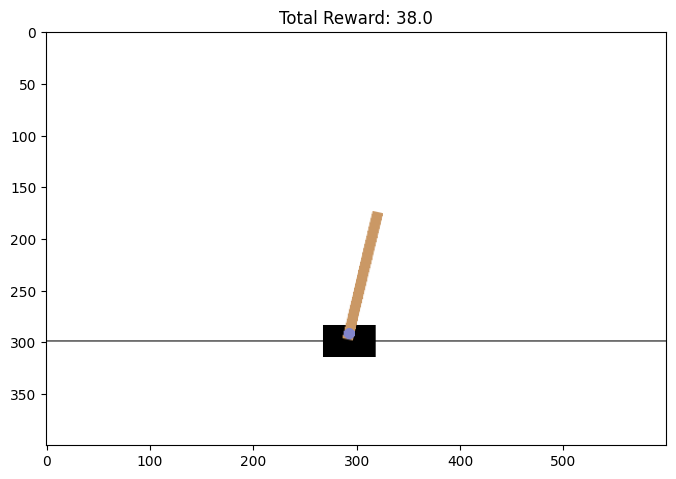
CartPole: 막대기를 수직으로 세우고 균형을 맞추는 환경
MountainCar: 두 개의 경사를 오르며 목표를 향해 움직이는 환경
Atari Games: 다양한 아타리 게임을 강화학습 환경으로 제공

강화학습 실습 환경 설정 및 기본 사용법

강화학습을 실습하려면 먼저 Python 환경을 설정하고 라이브러리를 설치해야 합니다. 여기서는 OpenAI Gym을 사용하여 실습 환경을 설정하는 방법을 소개합니다.

1. Python 환경 설정

Python 설치: Python 3.6 이상의 버전이 필요합니다.
필요한 라이브러리 설치:
- gym: OpenAI Gym을 설치합니다.

!pip install gym

import gym
import matplotlib.pyplot as plt
from IPython.display import display, clear_output

# 환경 생성
env = gym.make('CartPole-v1')

# 환경 초기화
state = env.reset()

# 환경 시뮬레이션 실행
done = False
total_reward = 0

# 시각화를 위한 설정
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111)

while not done:
    # 랜덤 행동 선택
    action = env.action_space.sample()  # 행동을 랜덤으로 선택

    # 환경에 행동을 적용하고 결과를 받음
    next_state, reward, done, info = env.step(action)

    # 총 보상에 추가
    total_reward += reward

    # 화면에 환경을 렌더링 (matplotlib 사용)
    ax.clear()
    ax.imshow(env.render(mode='rgb_array'))  # 화면을 이미지로 반환
    ax.set_title(f"Total Reward: {total_reward}")
    display(fig)

    # 이전 출력 지우기
    clear_output(wait=True)

# 시뮬레이션 종료 후 총 보상 출력
print(f"총 보상: {total_reward}")

# 환경 종료
env.close()

김민수

인공지능을 공부하고 가르치는 김민수 강사입니다. 공부한 내용 및 수업 자료가 업로드 됩니다.