Pulse Code Modulation(PCM)
- Most basic analog-to-digital conversion scheme
- sample analog data
- Quantize signals
- Encode signals into digital bitsteam
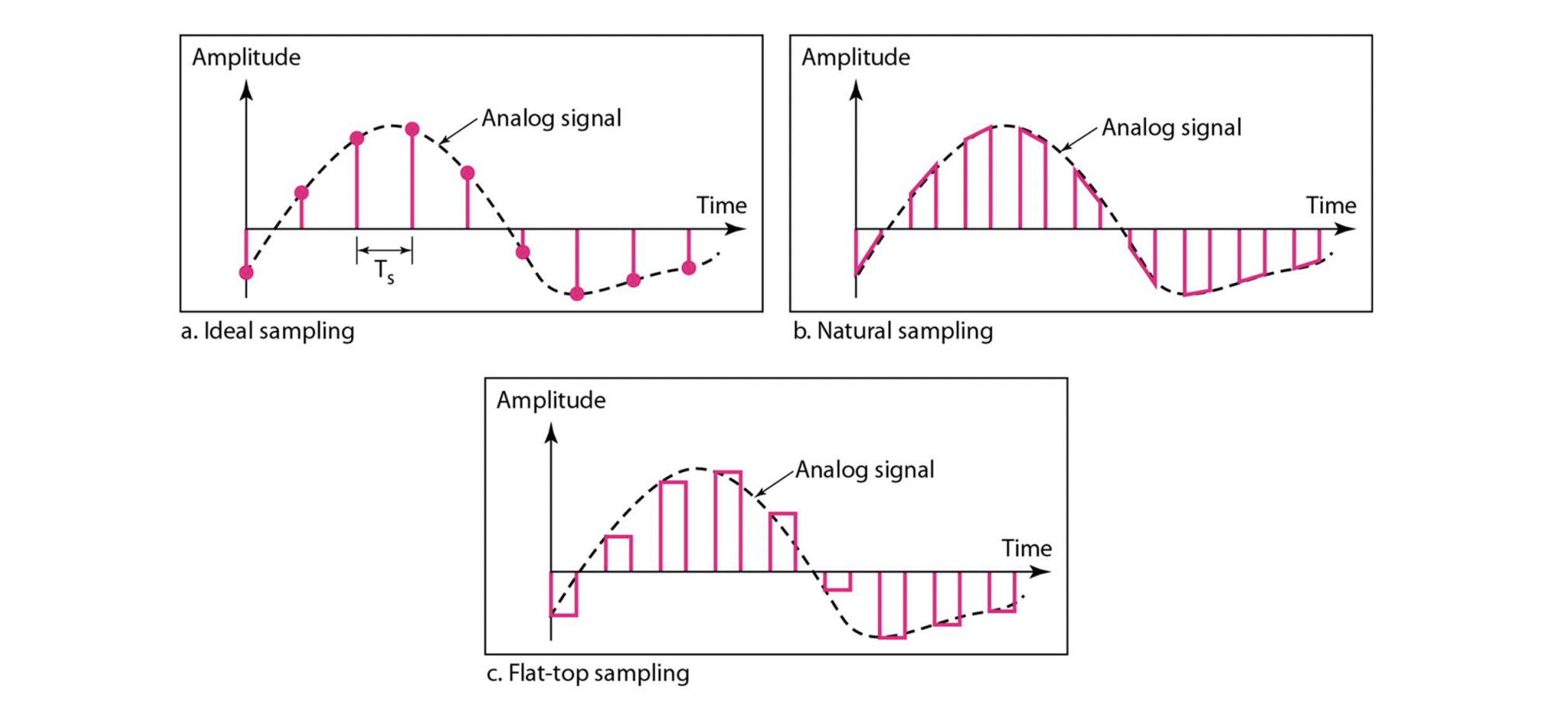
Sampling
- 주기적으로 signal amplitude를 읽는다.
- 주기는 내가 정한다. (sampling period)
- 그거 역수가 sampling rate
- sampling period x sampling rate = 1
- Nyquist theorem
: The sampling rate should be higher than twice the maximum frequency of the signal
(2배는 되어야 복원이 가능하다)
Q. Telephone companies digitize voice by assuming a maximum frequency of 4000Hz. What is the minimum sampling rate?
A. 8000Hz
Q. A complex low-pass signal has a bandwidth of 200kHz. What is the minimum sampling rate for this signal?
A. 400kHz
Quantizing
- The scheme to determine signal levels in a discrete manner
- The sampled signal level can be anywhere between minimum and maximum amplitude
- We need to quantize the signal into discrete signal levels in order to encode them into a digital bit stream
- analog signal의 진폭이 Vmin부터 Vmax 사이라고 하자.
- (Vmin, Vmax) 범위를 size D, L section으로 나눠라
- D = (Vmax - Vmin) / L
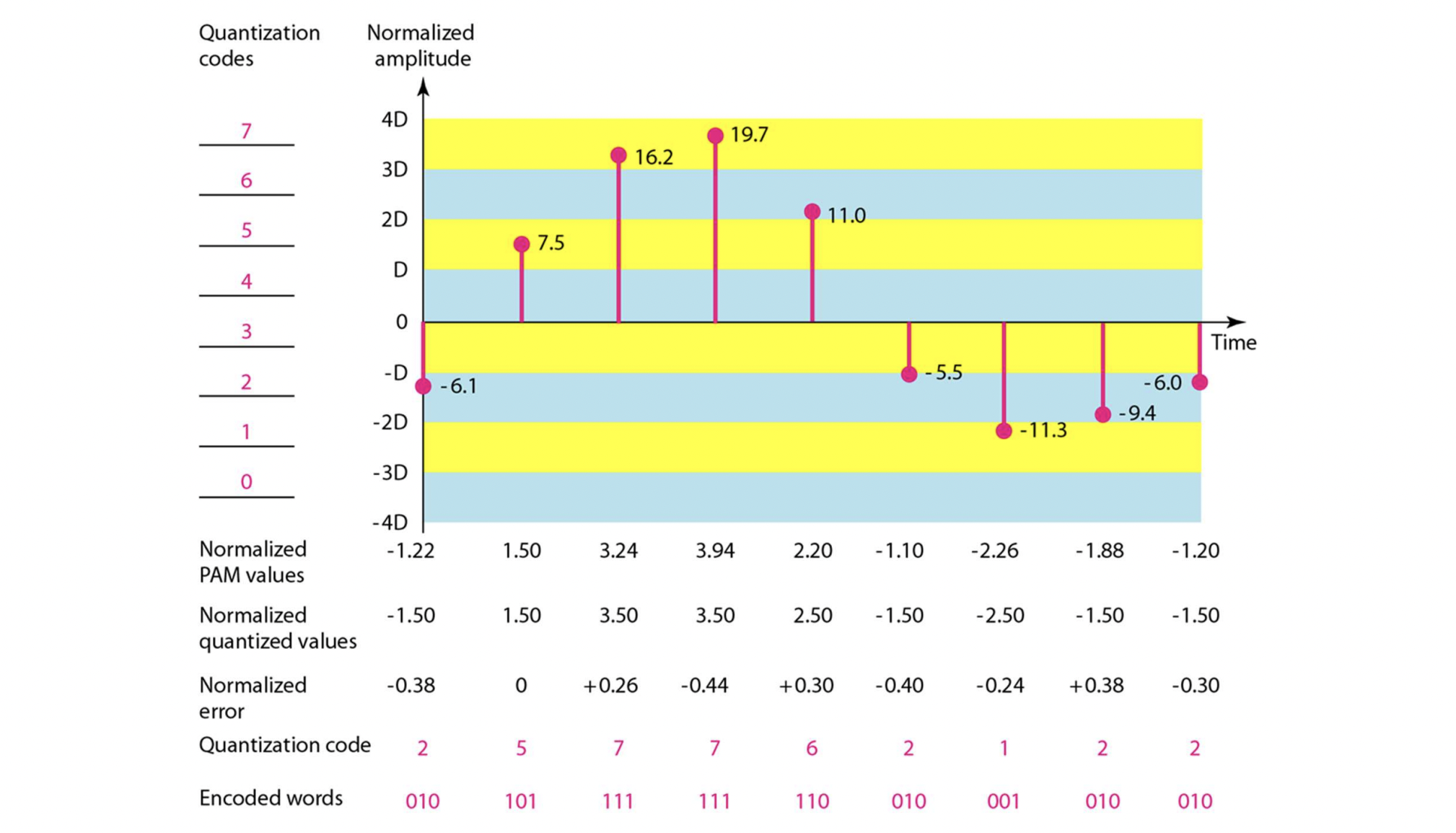
- D = 5. 하나의 점을 3bit로 해서 8개의 서로 다른 값을 갖도록 한다.
- 더 촘촘히 나누면 당연히 더 좋겠지. 그만큼 더 많은 bit가 필요하다. trade-off
- Quantization Error
- Difference between real value and quantized value
- -D/2 < error < D/2
- quantization level의 개수가 많아질수록, error는 줄어든다.
- SNRdB = 6.02nb + 1.76dB
nb : bits per sample
(X) Q. What is the SNRdB in the previous example?
(X) Q. A telephone subscriber line must have an SNRdB above 40. What is the minimum number of bits per sample
Encoding
- Convert quantized levels into bit patterns
- L개의 level이 있으면, nb = log2L
- Unit : bit rate
- Bit rate = sampling rate x nb
Q. 사람의 목소리를 digitize하려고 한다. 사람 목소리의 진동수는 0부터 4000Hz 사이이다. What is the bit rate, assuming 8 bits per sample?
A. Nyquist theorem에 의해, minimum sampling rate = 8000
8000 x 8 = 64000 bps = 64kbps