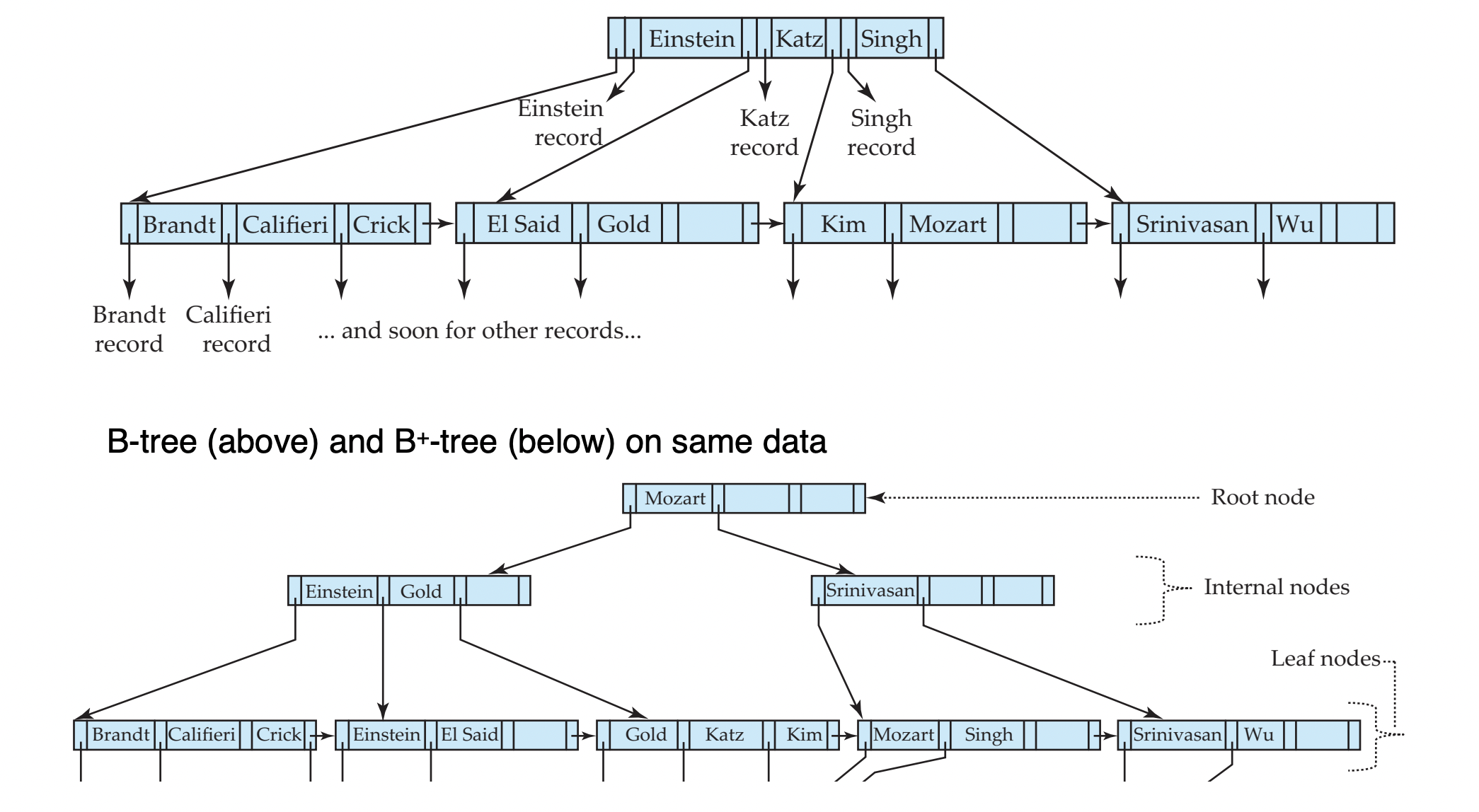
indexed-sequential file의 단점
- file size가 커질수록 성능이 저하된다 (overflow block이 계속 생긴다)
- file 전체에 대한 주기적인 reorganization이 필요하다
B+ tree index file의 장점
- insertion과 deletion이 발생했을 때,
small and local change로 자동으로 reorganization을 마친다. - 성능을 유지하기 위해 file 전체에 대한 reorganization이 필요하지 않다.
B+ tree index file의 약간 단점
- 애초에 B+ tree 자체가 추가적인 자료구조이기 때문에,
extra insertion and deletion overhead, space overhead
하지만, advantages of B+ tree outweigh disandvantages
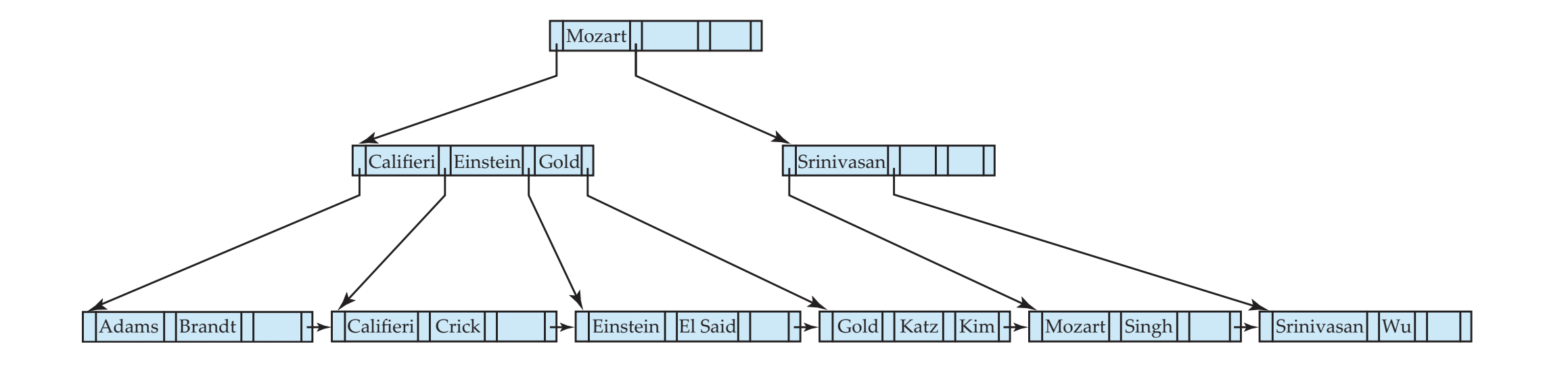
B+ Tree
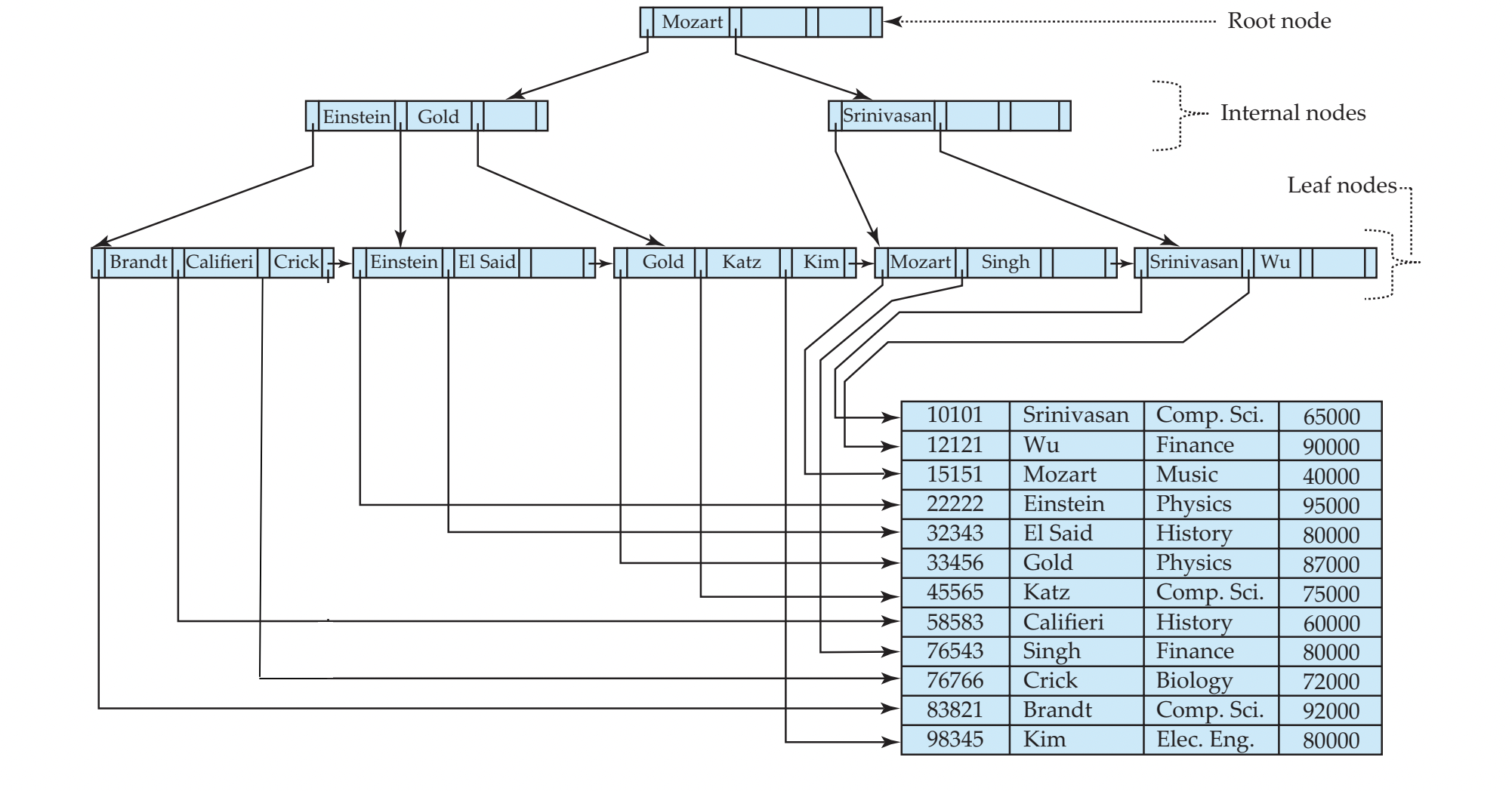
- binary search tree의 일반화 느낌
Properties
-
root에서 leaf까지 모든 path가 같은 길이 (height balenced tree)
-
root나 leaf가 아닌 node는 반드시
ceil(n/2) ≤ child node 개수 ≤ n -
leaf node는
ceil(n-1/2) ≤ child node 개수 ≤ n-1 -
If root is NOT a leaf,
최소 2개의 child node를 갖는다 -
If root is a leaf, (there is NO other nodes in the tree)
**0 ≤ child node 개수 ≤ n-1
Structure

-
Ki : search-key value
-
Pi : pointer to children (for non-leaf node)
or pointer to records or bucket of records (for leaf node) -
search-key는 오름차순으로 정렬되어있다. (중복 값은 없다고 가정한다)
K1 < K2 < ... < Kn-1
Leaf Node
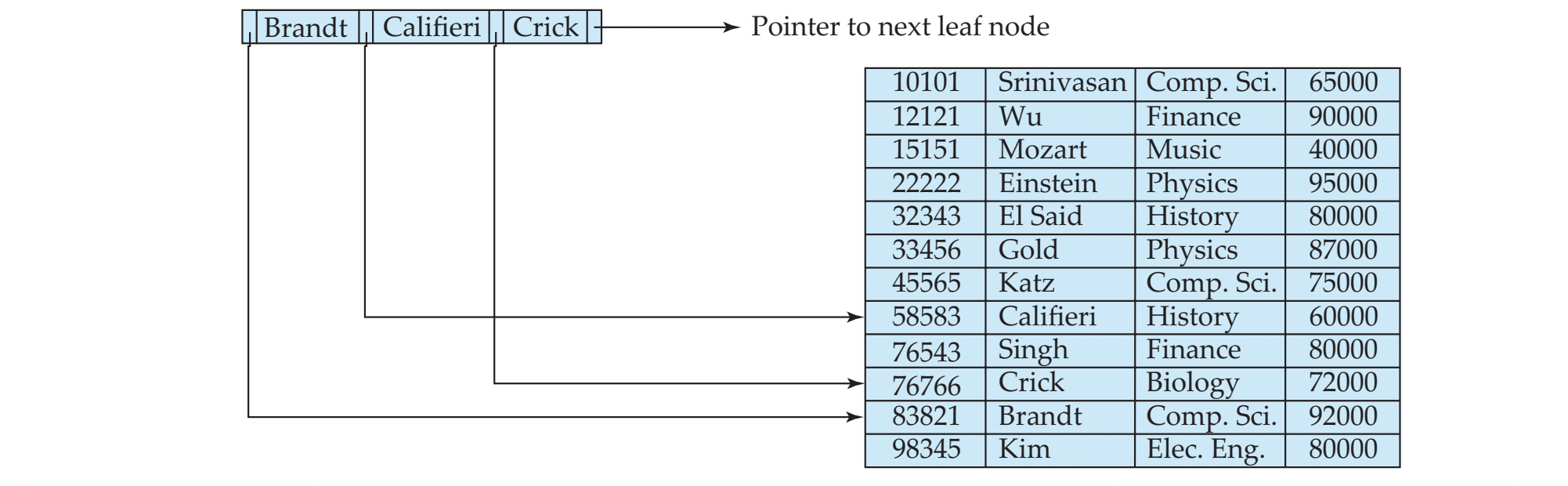
- Pi는 Ki에 대한 file record를 point한다
- i < j이면, search key value는 i ≤ j이다.
(일단 중복 없다고 가정했으니까 아예 작다고 하면 될 듯) - 마지막 Pn은 next leaf node를 point한다
Non-Leaf Node
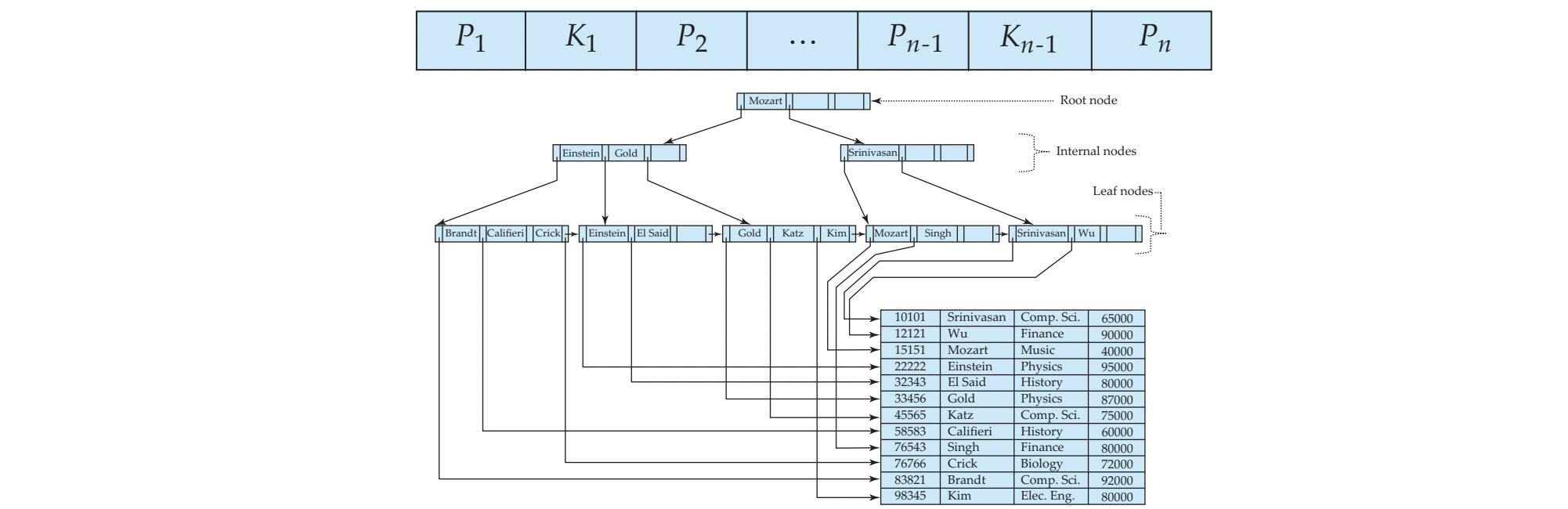
Non leaf node는 leaf node에 대해 multi-level sparse index를 형성한다.
- P1이 point하는 subtree의 모든 search key 값은 K1보다 작다.
- Pi가 point하는 subtree의 모든 search key 값은
Ki-1보다 크거나 같고 Ki보다 작다 - Pn이 point하는 subtree의 모든 search key 값은 Kn-1보다 크거나 같다.
Observation about B+ trees
-
서로 붙어있는 node끼리의 연결이 pointer로 이루어져 있기 때문에,
"logically" close blocks need NOT be "physically" close -
Non-leaf level은 sparse indices의 계층을 형성한다
- B+ tree는 비교적 작은 level 개수를 갖는다.
- root 바로 아래에 있는 level은 최소 2 * ceil(n/2) values
- 그 아래에 있는 level은 최소 2 * ceil(n/2) * ceil(n/2) values
- ...
- 이런 식으로 내려가면, tree의 height(depth)는 최대
- tree의 depth가 보장된다는 의미
- disk I/O는 tree depth만큼 발생하게 된다.
즉, worst case가 보장된다.
안정적인 성능을 보장한다고 할 수 있다 - Thus, searches can be conducted efficiently
- disk I/O는 tree depth만큼 발생하게 된다.
Query
Find
function find(v) { // v(search key) 찾는다
C = root
while (C is NOT a leaf node) {
Let i be least number such that v ≤ Ki
if (there is NO such number i) // 얘보다 큰 search key가 없다
Set C = last non-null pointer in C // 맨 오른쪽 pointer
else if (v = C.Ki) // 값이 같아
Set C = Pi+1 // 오른쪽 pointer
else
Set C = C.Pi // 왼쪽 pointer
}
if for some i, Ki = v
return C.Pi
else
return null
}Range
- find all records with search key in a given range
/*returns all records ith search key value V such that lb ≤ V ≤ ub*/
function findRange(lb, ub) {
Set resultSet = {};
Set C = root node
while (C is NOT a leaf node) {
Let i = least number such that lb ≤ C.Ki // lb보다 큰 애중에 가장 작은거
if (there is NO such number i) // 얘보다 큰 애가 없어
Set C = last non-null pointer in C
else if (lb = C.Ki)
Set C = C.Pi+1
else
Set C = C.Pi
}
/*여 위에는 그냥 find랑 똑같다*/
/*지금부터 C는 leaf node*/
Let i be the least value such that lb ≤ C.Ki
if (there is NO such i) // 현재 노드들 중에 가장 커
then Set i = 1 + number of keys in C // 다음 노드로 넘어가자
Set done = false
while (not done) {
Let n = number of keys in C
if (i <= n and C.Ki <= ub) // ub보다 작은 애들을 resultSet에 추가해
Add C.Pi to resultSet
Set i = i+1
else if (i <= n and C.Ki > ub) // ub보다 더 큰 애가 나왔어
Set done = true
else if (i > n and C.Pn+1 is NOT null) // 노드에 있는 애들 다 비교했는데 size보다 커졌어
Set C = C.Pn+1 and i = 1 // 다음 노드로 넘어가자
else
Set done = true // 더 이상 넘어갈 노드가 없다
}
return resultSet
}
- I/O 횟수를 계산하라고 하면, access한 block의 개수를 세면 된다
(ppt 필기 참고)
Non-Unique Keys
- search key ai가 unique하지 않으면, 새로운 index를 만든다 :
composite key (ai, Ap), which is unique
key의 pair가 unique하게 만든다- Ap는 primary key도 되고, 다른 attribute도 상관 없다.
단, uniqueness만 보장해주면 된다
- Ap는 primary key도 되고, 다른 attribute도 상관 없다.
- ai = v를 searching하는 건 composite key에 대한 range search로 구현할 수 있다.
range : (v, -∞) to (v, + ∞)
- More I/O operations are needed to fetch the actual records
- If the index is clustering, all accesses are sequential
- If the index is non-clustering, each record access may need an I/O operation (여기저기 흩어져 있기 때문에, 추가적인 I/O가 랜덤으로 발생한다)
Updates on B+ Tree
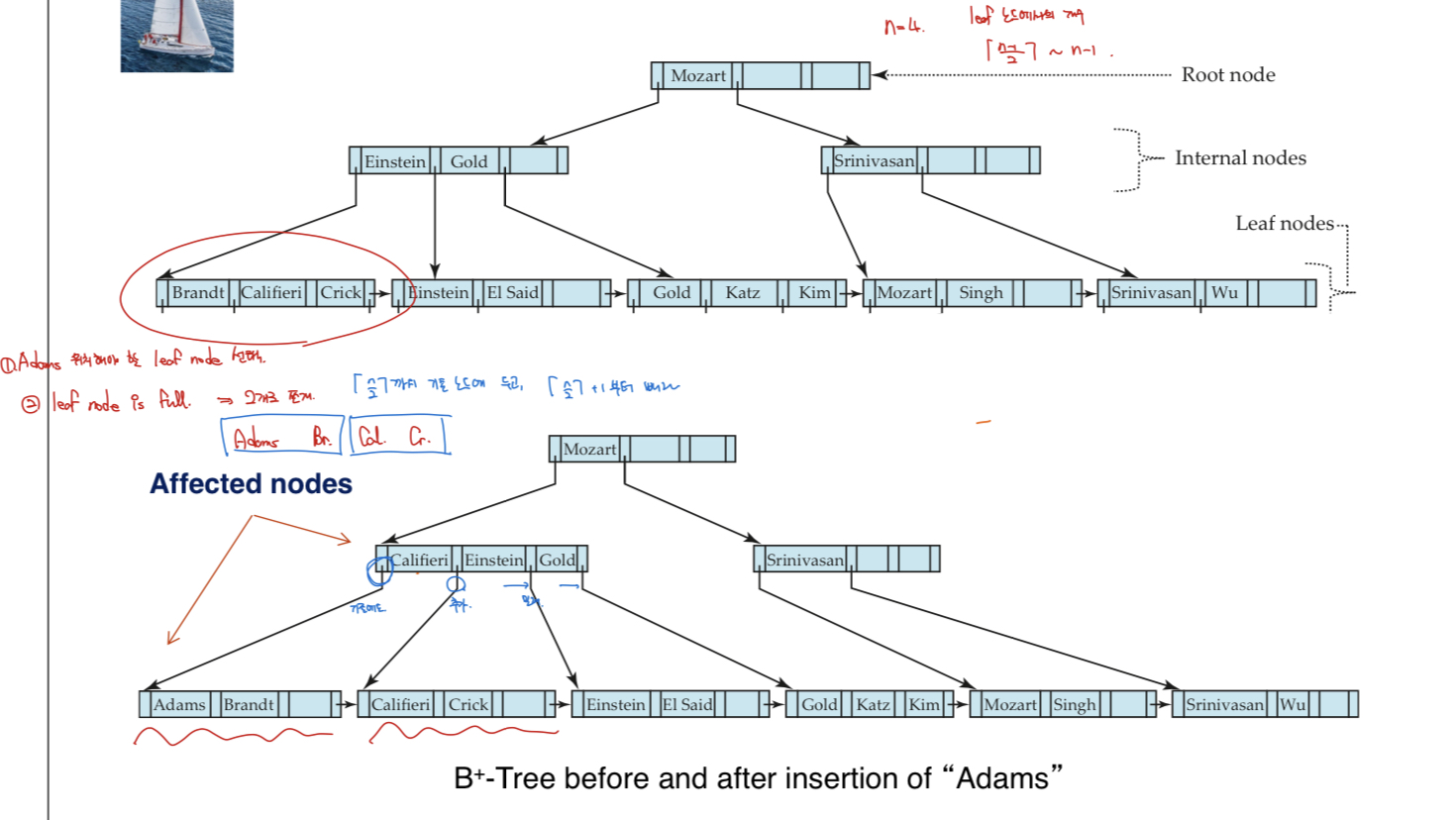
Insertion
추가해야 할 record가 file에는 이미 올라갔다고 가정하자.
- pr : pointer to the record,
- v : search key value of the record
- search key value가 들어가야 할 leaf node를 찾고,
- 공간이 있으면 insert (v, pr) pair in the leaf node
- 그렇지 않으면 (leaf node가 꽉 차있으면),
(1). node를 쪼개(split)고, (2). parent node도 update
Splitting a leaf node

- 우선 n개의 pair ( (v, pr) 포함 )를 정렬시킨다
- K 기준으로
(1, ..., ceil(n/2) )는 기존 노드,
(ceil(n/2) + 1, ..., n )은 새로운 노드로 만든다.
- 그럼 새로운 노드의 맨 앞에 있는 search key value와,
그 새로운 노드를 가리키는 pointer를 pair로 만들어서
parent node에 추가한다
- 만약에, parent도 꽉 차있으면, parent도 쪼갠다 -> 방법 곧 나옴
(propagate the split further up)
- 계속 올라가다라 root까지 꽉 차있으면,
root 쪼개고 새로운 root를 만든다
이 때, height는 1 증가한다
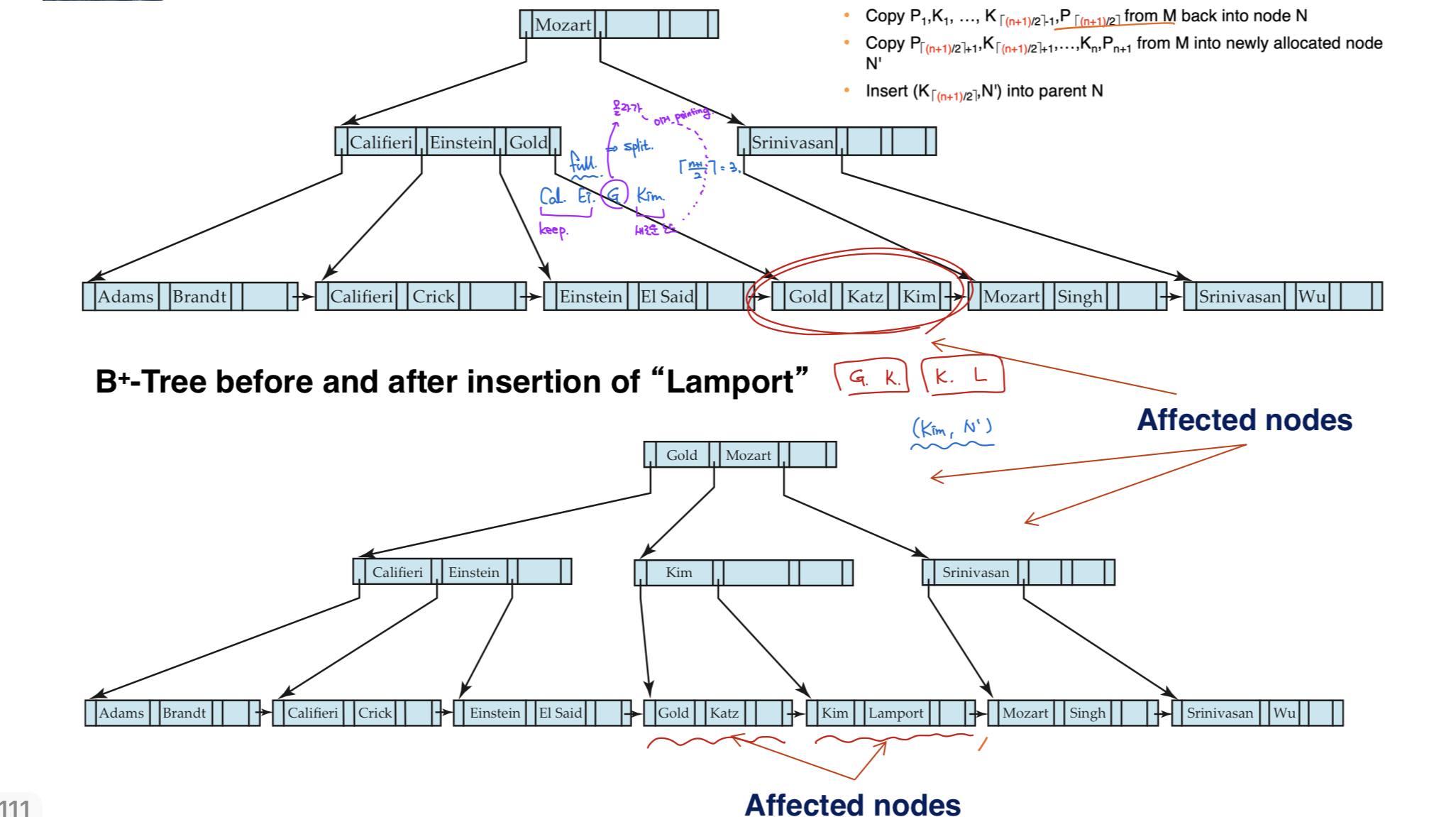
Splitting a non-leaf node
- K 기준으로
(1, ..., ceil(n+1/2) - 1)는 기존 노드
ceil(n+1/2)는 위로 올릴 pair
(ceil(n+1/2) + 1, ..., n)은 새로운 노드
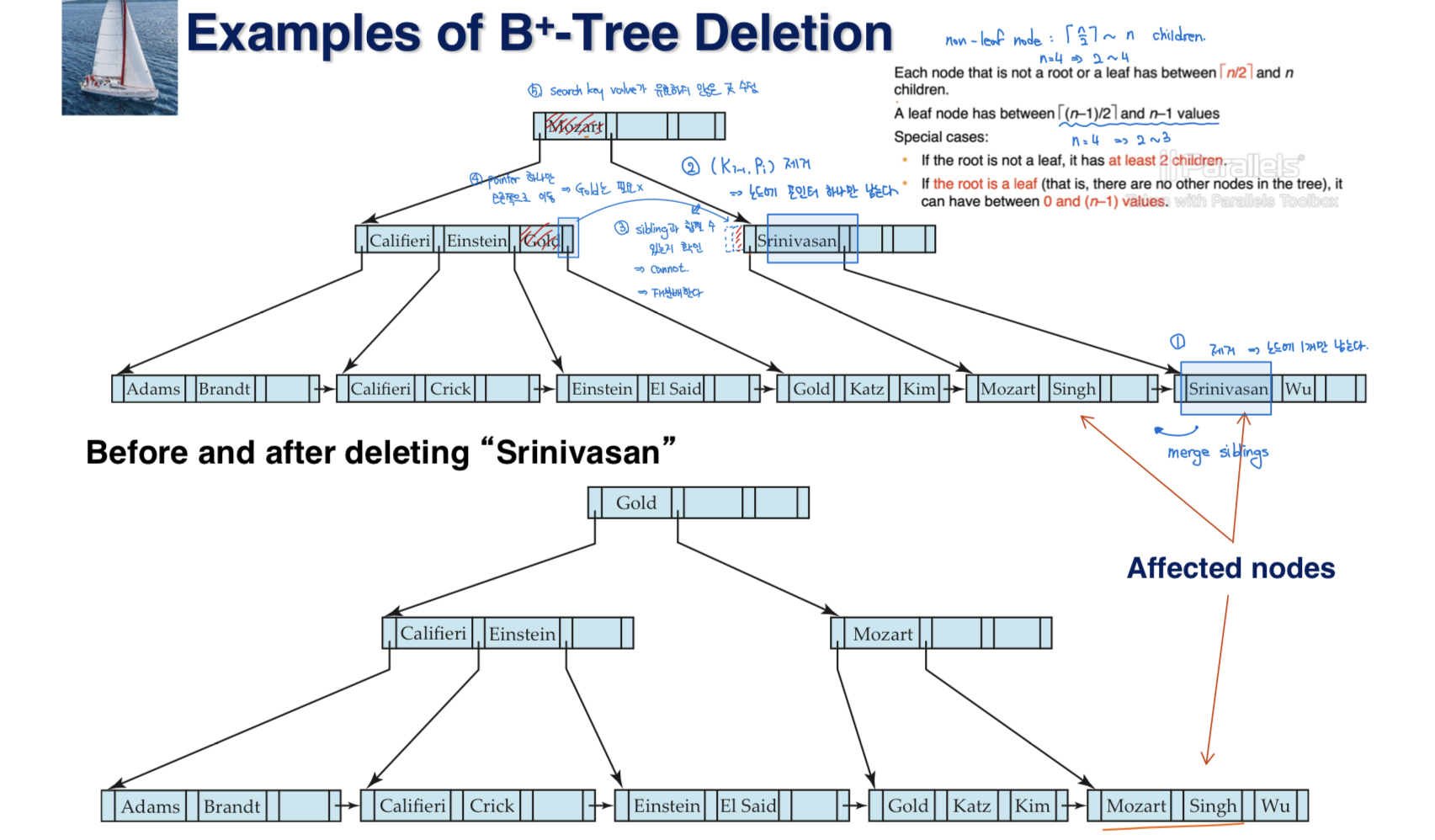
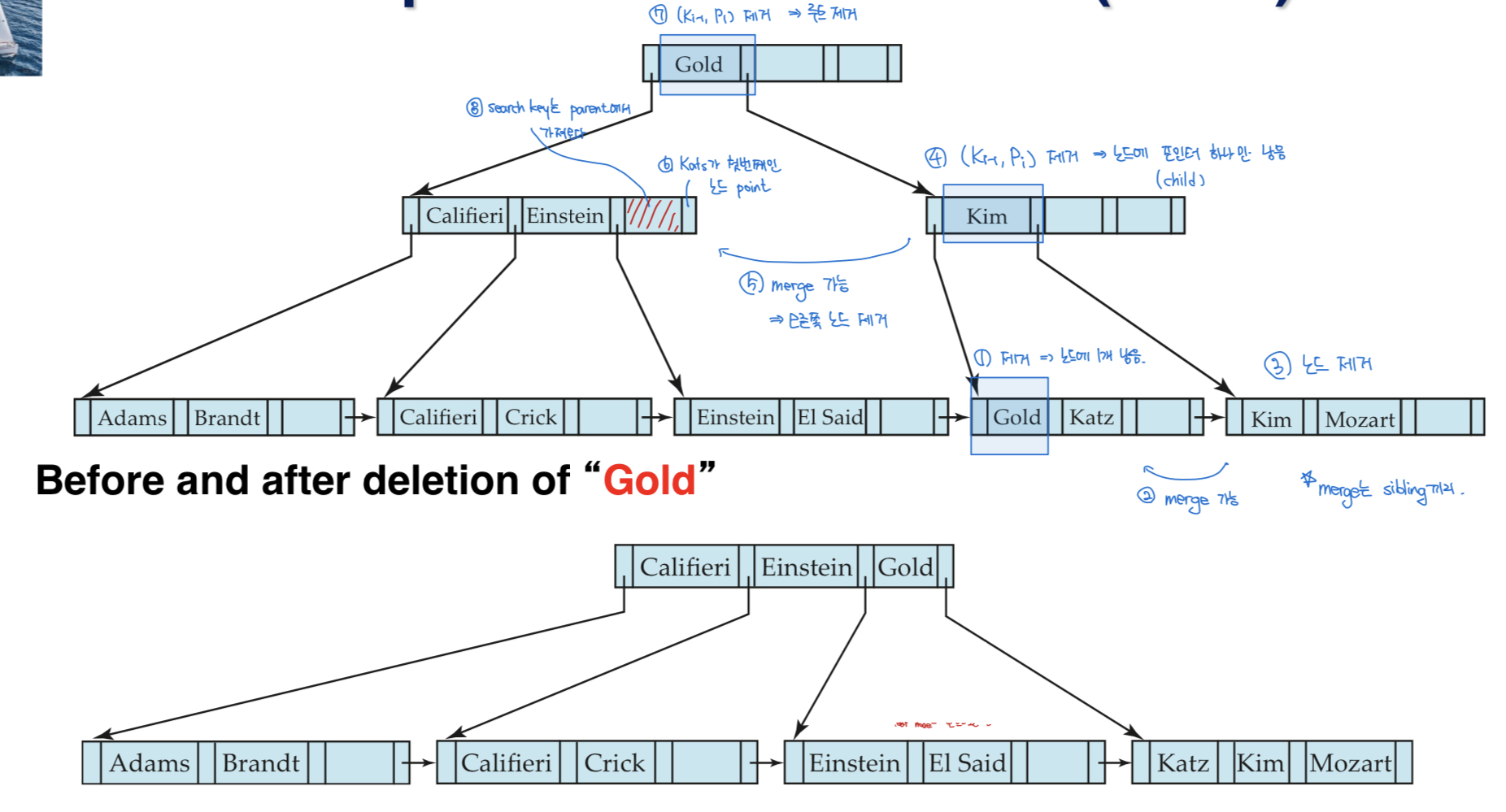
Deletion
삭제해야할 record가 file에서는 이미 삭제되었다고 가정하자
remove (pr, v) from the leaf node - 헷갈리게 왜 순서를 바꿔놨냐...
- 만약 pair를 제거함으로써 노드가 너무 적은 entry를 갖게 된다면 sibling과 합친다. merge siblings
- 두 노드에 있는 모든 searche key value를 single node로 합친다. (왼쪽으로 합친다). 그리고 나머지 노드를 제거한다.
- 부모 노드에서 pair(Ki-1, Pi)를 제거한다. Pi : 제거한 노드를 가리키는 pointer
- 마찬가지로 이런 식으로 계속 부모 노드로 올라가다 보면
root 노드가 제거될 수도 있다. (height -= 1)
- sibling과 합치려고 했는데 걔가 이미 full인 상황
-> 재분배 (redistribute)- 각 노드가 최소 entry를 갖도록 재분배한다.
- parent 노드의 search key value를 수정한다
Example
Example
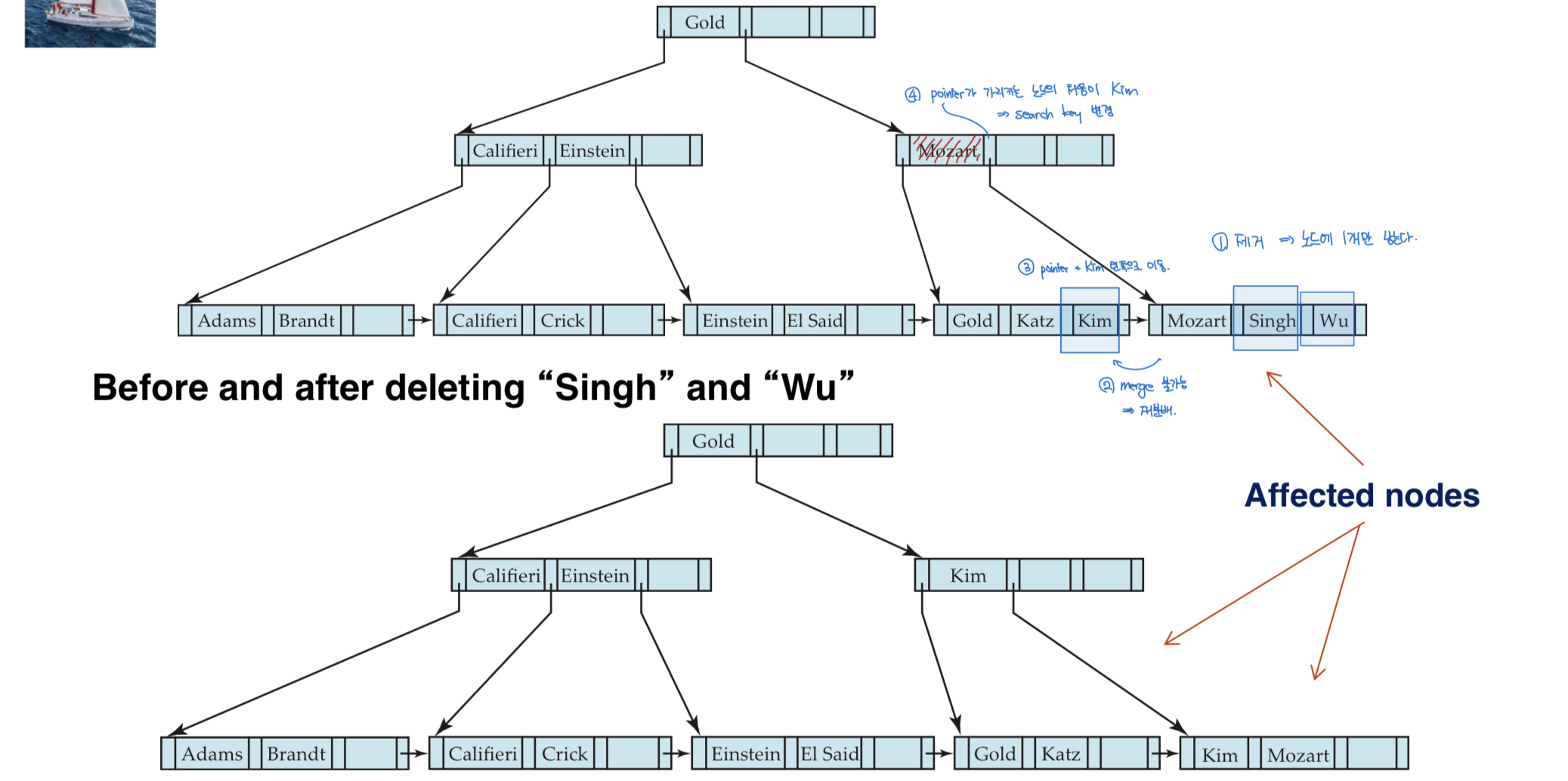
Example
Complexity of Update
- disk I/O 측면에서 insertion과 deletion의 cost는
최악의 경우 (worst case) tree의 depth와 같다.- 즉, K개의 entry와 maximum n에 대해,
- 즉, K개의 entry와 maximum n에 대해,
- 사실 노드는 대부분 적당히 채워져 있어서, split과 merge는 매우 드물게 일어난다.
- insertion order에 따라 node의 채워짐 정도가 달라지는데,
random으로 들어오면 2/3 정도,
sorted order로 들어오면 1/2 정도가 채워져 있다.
B+ Tree File Organization
- leaf node가 pointer가 아닌, 실제 record를 저장한다
- keep data records clustered when updating
- leaf node는 절반은 채워져 있어야 한다.
- record가 pointe보다 훨씬 많기 때문에,
leaf node에 들어가야 하는 record의 maximum number는
nonleaf node의 pointer 개수보다 적다
- record가 pointe보다 훨씬 많기 때문에,
- insetion과 deletion은 B+ tree index에서와 동일하다
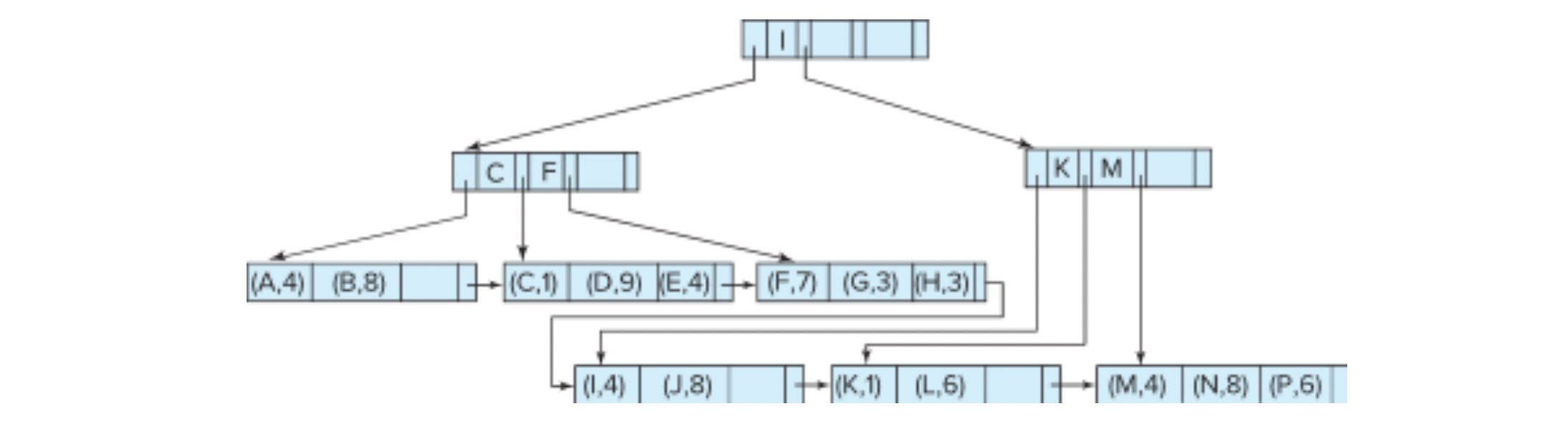
- B+ tree index에서는 3개 entry에 접근하려면 3번의 I/O가 발생했는데,
여기서는 만약 3개가 같은 노드에 있으면 1번의 I/O로 충분히 값을 가져올 수 있다
Other Issue in Indexing
Record relocation and secondary indices
- record가 움직이면 해당 record에 대한 pointer를 저장하는 secondary indices도 update되어야 한다
- B+ tree file organizaiton에서 Node split은 매우 expensive하다
- Solution : secondary index의 record pointer를 이용하는 대신
B+ tree file organizaion의 search key를 이용한다 - 즉, secondary index의 pointer 자리에 실제 data 값은 저장하게 해서
차라리 tree를 두 번 탐색하게 한다.- Higher cost for queries, but node splits are cheap
Bulk Loading and Bottom-Up Build
- Inserting entries one-at-a-time into a B+ tree는
매 entry마다 1번 이상의 I/O를 요구한다 - large number of entries를 loading하기에는 매우 비효율적이다
Efficient Alternative 1
- entry들을 먼저 sorting하고, sorted order대로 insert한다
- 완성된 노드(왼쪽)에는 더 이상 접근하지 않는다.
- I/O performance를 향상시킨다
Efficient Alternative 2 : Bottom-up
- entry들을 먼저 sorting하고,
leaf level부터 시작해서 tree를 layer-by-layer 방식으로 만든다
B Tree Index Files
- B+ tree와 유사하나, search key value가 only once만 나타난다.
- additional pointer field for each search key in a non-leaf node
가 반드시 필요하다
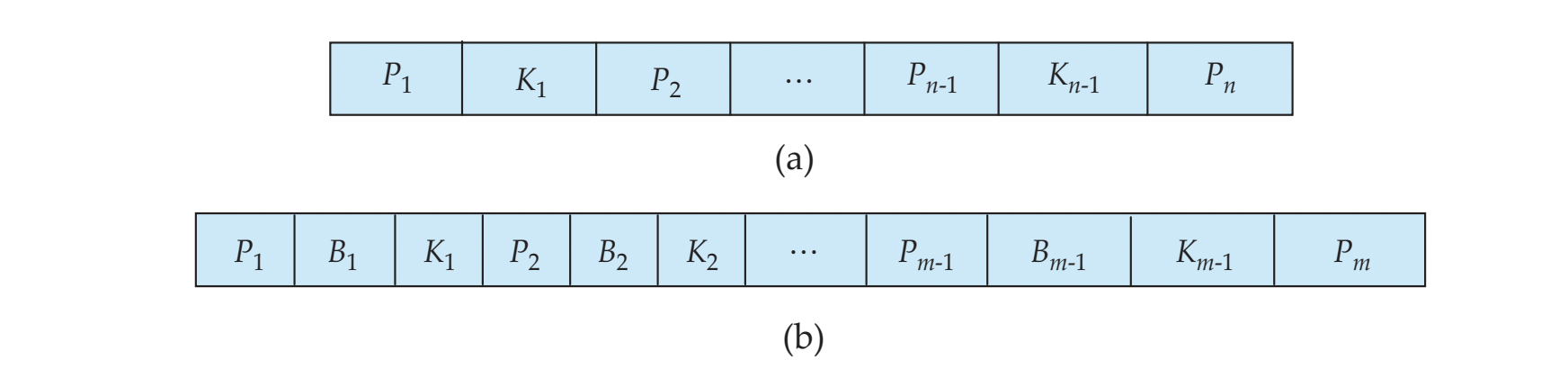
- (a) : leaf node
- (b) : non-leaf node
Advantage
- B+ tree에 비해 더 적은 node 개수를 갖는다
- leaf node에 닿기 전 searche key value를 찾을 수 있다.
Disadvantage
- 그래도 대부분 leaf node에서 발견된다
- non-leaf node가 커지기 때문에, tree의 depth가 더 커진다
- B+ tree에 비해 insertion과 deletion이 매우 복잡하다
- B+ tree에 비해 구현이 어렵다
Typically, advantages do NOT outweigh disadvantages