
Abstract
시계열 데이터는 시간에 따라 변하는 데이터를 분석하고 모델링하는 데 필수적인 영역입니다. 현재 널리 사용되는 딥러닝 모델로는 순환 신경망(RNN), 시계열 합성곱(CNN), 그리고 신경 미분 방정식(NDE)이 있습니다. 각각 고유한 강점과 계산 효율성을 제공하지만, 특정한 한계를 가지고 있습니다.
이에 따라 우리는 이들 접근 방식을 일반화하고, 단점을 보완하며, 제어 시스템에서 영감을 받은 간단하고 효율적인 시퀀스 모델을 제안합니다. 바로 선형 상태-공간 계층(Linear State-Space Layer, LSSL)입니다.
이론적 강점
LSSL은 다음과 같은 세 가지 주요 모델 계열과 밀접하게 관련되어 있습니다:
-
순환 신경망(RNN)
- 재귀적(recursive) 상태 갱신을 통해 입력 데이터를 순차적으로 처리합니다.
- RNN의 휴리스틱(예: 게이팅 메커니즘)의 수학적 근거를 설명할 수 있습니다.
-
시계열 합성곱(CNN)
- 선형 시불변 시스템(linear time-invariant system)의 특성을 활용하여 연속 시간으로 합성곱을 일반화합니다.
- 컨볼루션 필터를 사용해 병렬 처리와 계산 효율성을 제공합니다.
-
신경 미분 방정식(NDE)
- 시간 척도 조정(time-scale adaptation)과 같은 연속 시간 특성을 공유합니다.
- 데이터가 불규칙한 시간 간격으로 샘플링된 경우에도 효과적으로 작동할 수 있습니다.
장기 메모리 기능
LSSL은 연속 시간 메모리 구조에 관한 최근 이론을 통합 및 확장하여 장기 의존성(long-term dependency)을 학습할 수 있습니다. 이를 위해 LSSL은 구조화된 상태 행렬 ( A )의 학습 가능한 하위 집합을 도입합니다. 이러한 구조는:
- 상태 간의 관계를 효율적으로 모델링하며,
- 시계열 데이터에서 긴 시간 간격의 의존성을 포착하는 데 적합합니다.
LSSL modeling
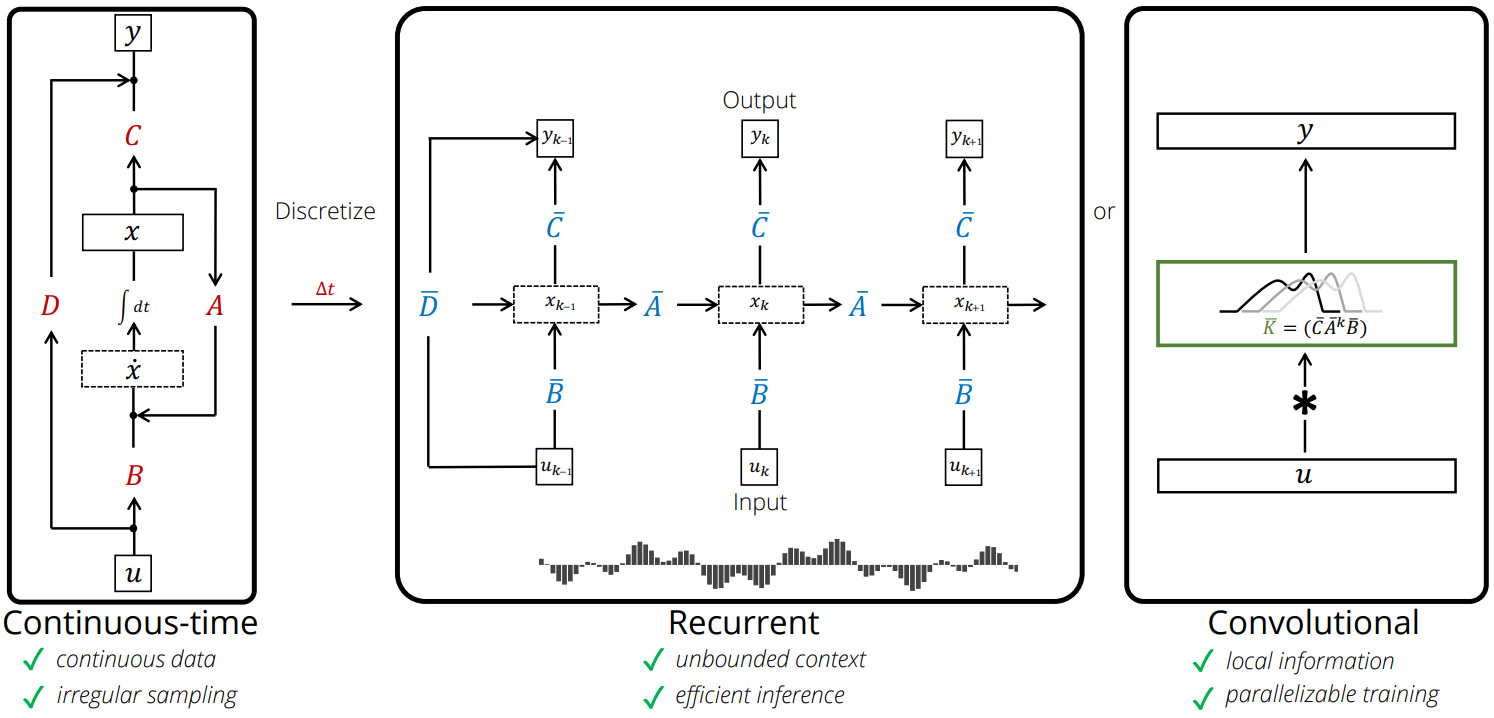
이전 모듈들의 발전은 모두 공통적으로 기존 CNN/RNN의 구조 및 단점을 time-step 차원에서 접근했다는 점이다. 하지만 이 방법들은 convolutional, recurrent model의 문제를 근본적으로 해결하지 못했다.
Linear-State-Space-Layer (LSSL)은 위의 그림에서 나오는 각각의 장점을 통합한 구조를 고안하는 것을 목적으로 삼았다.
계산식은 HiPPO의 접근과 차이가 거의 없다. LSSL은 1-dimentional function이나 sequence 를 implicit function 를 통해 mapping하는 방법임.
.
.
-
RNN 및 ODE의 장점 계승:
- RNN에서 나타나는 장기 종속성(long dependency)을 처리할 수 있음.
- ODE 기반 시스템처럼 연속적인 상태 변화를 학습할 수 있음.
-
State Matrix 의 역할:
- 는 시스템의 변화를 주도하는 학습 행렬로, 메모리와 장기 종속성을 모두 고려.
- HiPPO(Highly Optimized Projection Operator)와 같은 이전 연구에서 사용된 아이디어를 기반으로, 연속 시간 데이터의 메모리를 효과적으로 처리.
LSSL은 기존 CNN과 RNN의 한계를 극복하며, 다음과 같은 특징을 가집니다:
- 모든 형태의 1-D Convolution을 표현할 수 있는 범용적인 모델입니다.
- 적절한 step size()와 state matrix()를 활용해 RNN 및 ODE의 장점을 계승할 수 있습니다.
- 병렬 처리와 빠른 학습이 가능하며, 연속 시간 데이터를 효과적으로 처리할 수 있습니다.
이를 통해 LSSL은 제어 이론에서 잘 알려진 방법론을 활용해 CNN과 RNN의 구조적 한계를 넘어서며, 새로운 형태의 시계열 및 1-D 데이터 처리를 가능하게 합니다.
Background
Continuous time memorization에 대한 근사화는 HiPPO, LSSL논문에서 공통적으로 가지는 기술적 배경이다.
Continuous time으로 모델링을 할 수 없기 때문에 이를 이산시간 모델로 근사화 하는 것이다. 연속 시간 미분방적식 를 얼마나 조정하느냐에 따라 성능이 달라진다고 한다. 결국 연속 시간 모델을 이산화할때 를 조정하는 것이 중요하다.
LSSL의 수식을 보기 이전에 필요한 지식들에 대해서 먼저 소개하겠다.
Picard iteration
모든 형태의 differential equation 는 integral equation 를 동치로 가진다. 이 integral solution은 x의 근사값을 에 넣고 계속 연산을 하며 풀어나갈 수 있다.
picard iteration?
천천히 생각해보면 를 이항하면
로 표현이 가능하다.
generalized bilinear transform (GBT)
이산화 과정에 대해 직접 적분할 수가 없기 때문에 Discrete times 에 대해, 를 쪼개서 얻어야 한다. (만약 closed form을 알지 못한다면, 여기서 Picard iteration이 쓰일 수 있음.)
다른 방법으로는 GBT가 있는데 Linear ODE에 적용될 수 있는 방법이다. HiPPO 리뷰에서도 쓰인 방법이다.
풀고자하는 ODE가 다음과 같을 때
.
.
GBT update는 다음의 수식으롤 진행된다. 수식의 는 step size를 의미한다.
.
처음에는 이 수식을 보고 뭔가 했지만 에 0을 집어넣어보면

이와 같이 Euler's method가 나온다는 것을 알 수 있고
에 1을 집어넣어보면 backward Euler's method가 나온다.
유도 과정
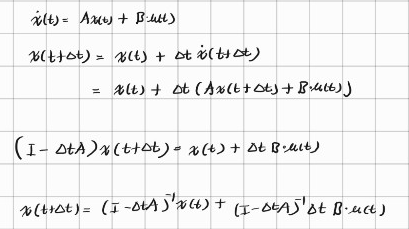
(글씨를 너무 못쓴다..)
따라서 를 조정함으로써 다음 time step인 +1의 기울기 값을 구하는 시점을 바꾼다는 것을 알 수 있다.
왜 이렇게 할까? -> 논문에서 을 사용했는데 서로 다른 시점의 도함수를 사용하기 때문에 곡률이 큰 (복잡한) 함수의 솔루션을 구하는 상황에서 좀 더 안정적인 예측이 가능하다. 이 방식을 bilinear라고 한다.
이렇게 bilinear 방식에 사용되는 A와 B를 라고 했을 때, 이 시스템을 Discretize하면 다음과 같은 SSM을 얻을 수 있다.
.
참고로 이다.
Timescale factor
- 가 커질수록 (시간 간격이 길어질 수록) 작은 시간간격에서보다 이전 정보의 세밀한 영향을 반영하기가 어렵다.
- ODE기반 RNN에서는 시간간격 가 고정되어 있어, 시간변화에 따른 정보를 바꿀 수 없다.
- 원본의 RNN(GRU, LSTM 등)은 gating 매커니즘(forget gate, input gate 등)을 통해 어떤 정보를 유지할지 학습한다.( 를 조정하는 것과 비슷하다고 볼 수 있을 것 같다. )
- CNN관점에서 는 convolution kernel의 크기를 조절하는 형태로 해석이 가능하다. ( 의 값이 크면 처리해야 될 정보의 양이 더 많기 때문에 kernel size가 큰 것으로 해석이 가능할 것 같다. )
Timescale factor
입력되는 함수 와 고정된 probability measure 가 있을 때, 함수의 기본꼴인 개의 basis가 있다고 가정해보자. 각 time step t마다 이전까지의 input인 는 N개의 basis조합으로 표현이 가능하다. 이는 함수를 projection해서 획득한 coefficient vector 를 통해 나타낼 수 있다. 이때 time step t는 measure 에 의존하게 된다. 를 통해 원본함수인 를 나타낼 수 있는 것이다. 이것을 HiPPO라고 한다.
HiPPO의 경우에는 두 가지 경우(해당 논문에서는 LegT, LagT라는 이름으로 제안된 메트릭)를 제안하였는데, 모든 time step에 같은 중요도를 매핑하는 uniform measure 와, 가까운 time step에 보다 높은 중요도를 매핑하는 exponential-decaying measure
가 있다. 둘의 공통점은 window 안에서 균일한 measure weight을 가진다는 점이지만, LegS는 시간이 흐를수록 window 크기가 커진다는 차이점이 있다. 아무튼 중요한 점은 measure 종류에 따라 matrix A를 closed form으로 풀어낼 수 있으며, 이를 토대로 long dependency에 대한 모델링이 가능하다.
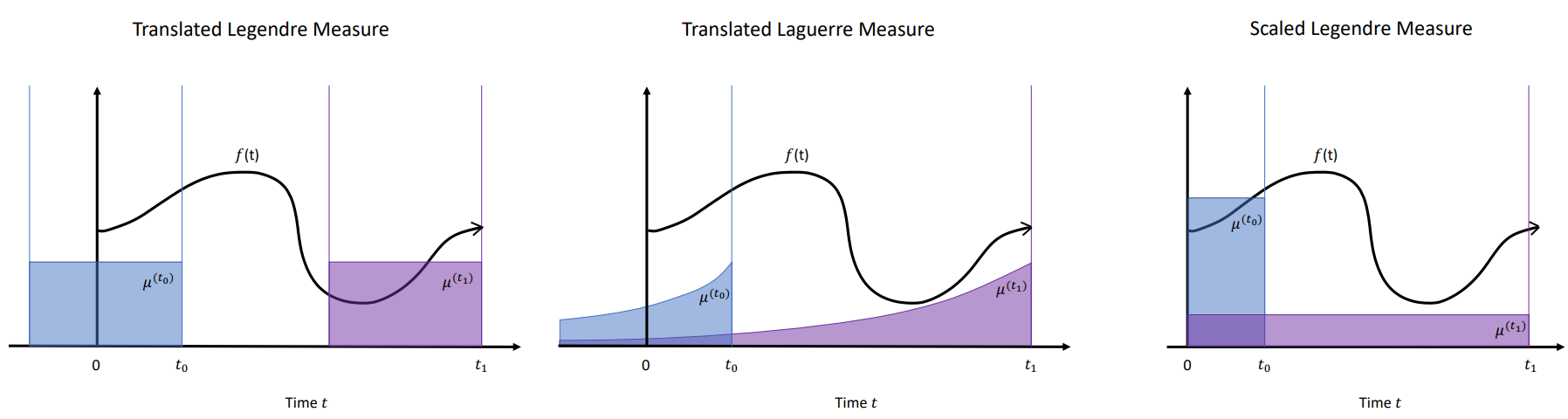
를 힐베르트 공간에 projection한 함수의 계수(coefficient vector)를 구하는 것과 Legendre Polynomials에서 measure를 scaled and shift하는 과정은 이전 HiPPO논문에서 했기 때문에 여기서는 Translated Legendre만 소개할 것이다.
Translated Legendre
Translated Legendre는 윈도우 크기가 이고 현재 지점이 t인 경우의 Legendre measure를 의미한다.
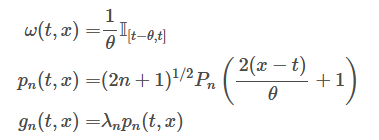
tilting 개념이 등장하면서 굳이 OP를 쓰지 않을 때 사용하는 함수가 등장한다. 이를 라고 하는데, 만약 대신 조합된 함수 형태인 를 쓴다고 가정하면 각 time step에서 에 orthogonal해진다.
(내적을 할때 이기 때문임.)
참고로 \omega(t)는 measure로 다항함수의 basis들이 서로 수직하도록 만들어주는 녀셕이다. 따라서 조합된 함수도 수직으로 맞춰줘야함. (그래서 가 되는 것! )
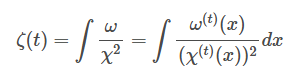
그래서 다음과 같은 형태가 나온다. 그리고 여기에 normalize를 해주는데 그렇게 된다면 measure는 는 를 density로 가진다. (OP를 orthonomal하게 맞춰주기 위함.)
Projection and Coefficients
tilting을 고려한 coefficient를 구하기 위해 원본함수를 measure에 projection하는 수식은 다음과 같다.
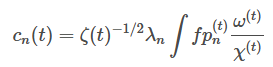
인 이유는 basis끼리의 내적이 아니라 원본함수와의 내적이기 때문에 가 한번 곱해지기 때문임.
여기 까지가 tilting을 적용한 projection의 내용이고 이 다음의 수식은 이전 포스트 HiPPO에서 살펴보면 될 것 같다. (matrix A를 구하는 과정이 자세하게 나와있다.)
LSSL해석
다시 LSSL로 돌아와서 Fixed state space representation 가 주어진 상황을 가정해보자. 간단하게도 LSSL은 input sequence를 output sequence로 매핑하는 과정이 된다. LSSL는 이러한 매핑 과정에서 파라미터 행렬 그리고 discretize에 필수적인 로 정의된다.
LSSL to RNN
LSSL에서의 recurrent state는 각 time step 로 계산이 된다.
현재 state는 , output 는 이산화된 LSSL formulation에 의해 계산된다.
.
따라서 RNN 구조와 같이 동작하는 것을 알 수 있다. 심지어 RNN 구조에서의 gated recurrence 도 만족한다. 1차원의 gated recurrence 구조와 동일하다.
LSSL to CNN
간단한 상황을 가정하기 위해 초기 상태를 으로 가정하자. 이러한 가정 하에 Linear State System의 출력을 다음과 같이 나타낼 수 있다:
이는 곧 discrete-time convolution으로 표현 가능하다.
여기서
따라서, LSSL은 출력이 convolution 연산에 의해 계산되는 모델로 해석 가능하며, 이때 convolution 연산은 FFT를 통해 가속화할 수 있다.
일반적인 continuous state-space system 관점에서, 출력 는 입력 와 시스템의 impulse response function 간의 convolution 연산으로 표현된다.
만약 convolutional filter가 rational functional degree 를 가지는 경우, 크기가 (N)인 state-space model로 필터를 나타낼 수 있다. 기존 연구들에 따르면, 임의의 convolutional filter (h)는 유한한 degree 값을 가지는 rational function으로 표현이 가능하다.
HiPPO matrix의 사례를 살펴보자. Translated Legendre의 경우를 보면, 는 특정 구간 내에서 동일한 확률 분포를 가지는 measure로 정의되었다.
일반적인 LSSL에서 를 고정시키면,
첫 번째 식은 history element를 기억하는 과정에 해당된다.
두 번째 식 은 해당 윈도우 내에서 유의미한 feature를 추출하는 작업이다.
따라서, LSSL은 결국 width가 학습 가능한 convolutional kernel filter를 학습하는 과정과 동치라고 생각할 수 있다.
Deep Linear State-System Layers
일반적인 LSSL은 간단하게 요약하면 입력 시퀀스를 출력 시퀀스로 매핑하는 시스템이었다. 예컨데 길이가 인 신호가 있다면,LSSL은 를 수행하는 하나의 vec to vec함수의 구조이다 이때 함수 자체는 parameterized되어있다. 만약 LSSL을 ψ라고 한다면,
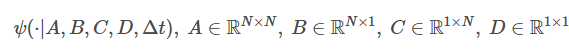
다음과 같이 표현할 수 있다. 이전에 말했던 것처럼 단일 LSSL은 Recurrence, Convolution의 특징을 모두 가지고 있어 RNN, CNN의 대표적인 레이어인 recurent unit이나 convolution kernel처럼 사용할 수 있다. 또한 입력 시퀀스가 transformer의 input처럼 의 hidden dimention을 가지고 있다면 LSSL은 만큼의 LSSL을 독립적으로 학습하게 되고, transformer의 multi-head 효과를 그대로 적용할 수 있다. (stacking함으로써 DNN과 동일하게 사용할 수 있음)
x 라면 L개의 Sequence를 처리하는데 H개의 LSSL을 쌓아서 처리한다는 말이다.
Discretized Linear system ODE에서, 시스템은 이산화된 parameter 가 계속 곱해지며 발전해간다.
.
그 말은 gradient descent로 학습하게 되면vanishing gradient 문제를 피할 수 없다는 것이다. 이처럼 만약 를 랜덤하게 초기화하고 학습한다면 성능이 안나온다는 말이다.
그래서 A를 초기화하는 방법으로 HiPPO를 쓴 것이다.
하지만 HiPPO의 문제점은 르장드르를 포함한 일부 measure에서만 이를 풀어낼 수 있는 structured solution matrix A가 존재했고, 모든 일반적인 measure에서도 다른 형태의 A가 존재함을 밝히지 못했다는 것이다.
따라서 LSSL에서는 이를 arbitrary measure 에서 미분 방정식을 찾을 수 있다고 증명하였다.
HiPPO와 LSSL 의미 정리
[HiPPO]
-
Continuous한 function을 어떻게 subspace g(t)로 잘 근사시킬 수 있는지가 주요 목표!
-
여기서 중요한 factor는 2가지 정도 있는데
-> 어떤 measure를 활용하여 projection 시킬 것인지,
-> 그리고 time window (step)을 어떻게 설정할 것인지.
-
time window에 따른 중요도와 weight를 적절하게 결정하기 위해서, LegS (scaled Legendre)를 제안함.
-
여러 증명들을 통해서, measures를 가지고 state space model을 구성하는 A와 B matrix가 어떤 수식을 갖는지 증명함.
-
A와 B를 가지고 Coef.에 대한 dynamic linear system을 품!
[LSSL]
-
A, B, C, D를 각각의 linear layer라고 두고 state space model을 디자인 함.
-
또한 time step과 A가 모델의 성능과 데이터셋을 예측하는데 중요한 역할을 한다는 것을 알아냄.
-
State space layers를 RNN과 CNN에 적용시킨 형태를 보여줌.
-
State matrix A가 학습 가능하도록 설정했을 때, HiPPO에서 제안한 state matrix A보다 성능이 더 잘 나올 수 있음을 보임.
결론
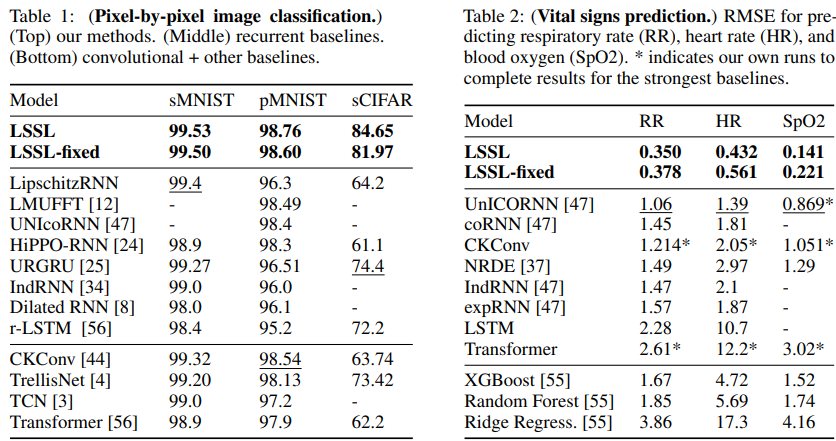
-
A를 HiPPO에서 정의한 matrix로 fixed한 것 보다 훈련시킨 것이 약간 더 높은 것을 알 수 있다!
-
그러나 실제로, 연산 메모리 문제 때문에 활용이 어렵다는 단점이 있다.
