
Abstract
시퀀스 모델링의 학습 목표는 LRD(Long Range Dependency)에 대한 다양한 모달리티와 작업에 걸쳐 시퀀스 데이터를 처리할 수 있는 단일 원칙 모델을 설계하는 것이다.
RNN과 CNN및 Transformer를 포함한 기존 모델은 LRD를 극복하기 위한 변형이 있지만 여전히 매우 긴 Sequence로 확장하기에는 어려움을 겪는다. 그래서 최근의 유망한 방식은 SSM(State Space Model)을 사용해서 시퀀스 모델링하는 것을 제안한다. HiPPO에서는 상태 행렬 A를 적절히 선택하면 LRD를 수학적으로 처리할 수 있다는 것을 보여주었고 LSSL에서는 이 행렬 A를 통해서 실제 모델을 만들었지만, 계산과 메모리 요구량이 불가능한 수준이었기 때문에 SSM을 새로운 방식으로 매개변수화 하는 것을 보여주는 S4방식을 제한한다. A를 수정함으로써 안정적으로 A matrix를 대각화하고 코시-커널을 사용해서 계산량을 줄인다.
전체적인 구조
수식이 매우 복잡하기 때문에 어떻게 구조를 변형시켰는지 먼저 보고 갈 것이다.
SSM을 정리하자면
SSM은 한마디로 LTI(Linear Time-Invarient) System으로 latent space를 구축하고자 하는 것이다. LTI시스템에서 미분 방정식을 구성하는 matrix가 시간불변성을 가진다는 것은 연속신호를 이산화한 관측에서 matrix는 변하지 않는다는 것이다. 즉 이론상 무한한 시퀀스 길이에 대해서 동일한 latent space 를 사용해서 output을 만들어 낼 수 있다는 것이다. RNN같이 연속적으로 들어오는 input을 사용해서 latent를 만드는 것이 아니라 시간 불변성이 성립하는 latent space가 있다면 아무리 오랜 시간이 흘러도 hidden space는 동일한 함수로 구현이 되는 것이다. 따라서 Long Range Dependency를 보장할 수 있는 것임.
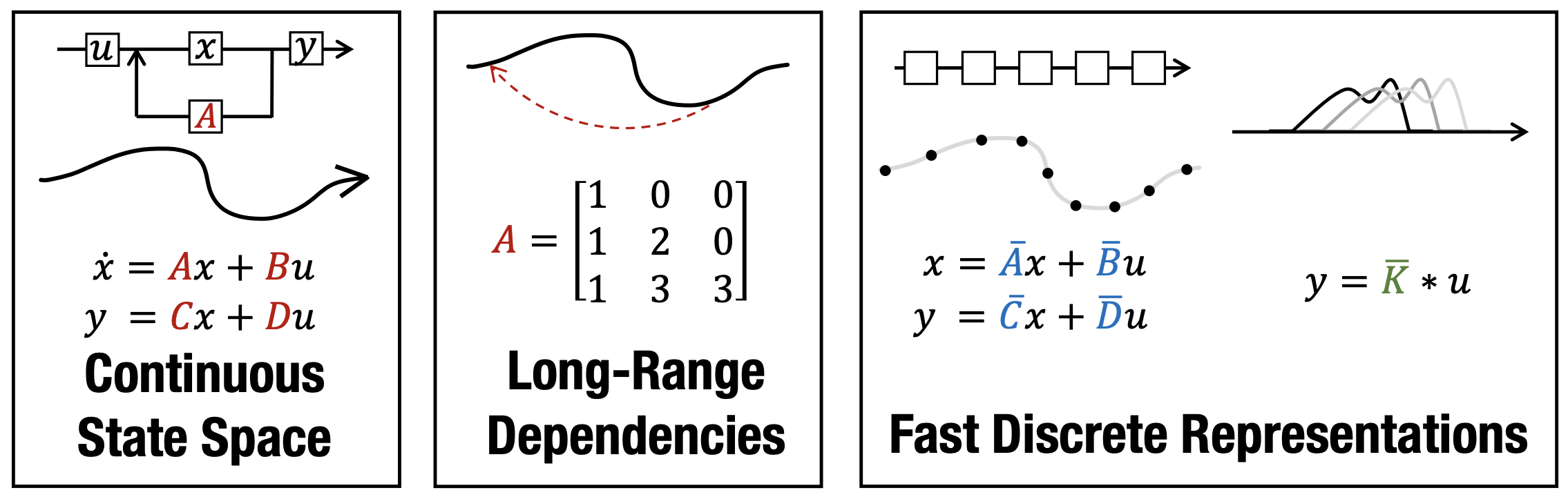
논문에 나와있는 그림을 보자. 맨 왼쪽에 SSM의 수식이 보일 것이다. 여기서 Continuous State Space부분에서 SSM구조에 해당하는 input 와 에 해당하는 Linear System의 상태가 보인다. (hidden state로 볼 수 있다.) 이 시스템을 통해서 출력값 를 내보내게 된다. 이때 가 지속적으로 변화하는 input에 대해서 저장하는 메모리 역할을 수행하게 된다면, 이론상 고정된 요소를 가진 행렬 에 대해서 꾸준히 이전 정보를 저장할 수 있게 되는 것이다. 이것이 중앙에 보이는 Long-Range Dependencies에 해당되고 실제로 구조화된 행렬에 대해서 효과성을 증명한 것이 바로 HiPPO이다.
이때 SSM은 Recurrent System이 되는데 Recurrent한 연산방식도 가능하지만, 단순화하여 convolution연산으로도 수행이 가능하다. 그러나 고차원 데이터에 대해서는 필연적으로 연산량이 증가하기 때문에 연산량이 높다는 문제가 생긴다.
Diagonalization (대각화)
행렬의 대각화는 행렬의 고윳값인 와 고유벡터(eigen vector)를 사용해서 대상이 되는 행렬은 고윳값이 대각선 성분인 행렬로 만드는 것이다. 대각화가 가능한 행렬 이 존재한다면, 이 행렬의 eigen value 와 eigen vector에 대해서 로 표현이 가능하다.
For eigenvalues and eignenvectors
이런 상황에서, 기존의 식을 조금 바꿔보면 다음과 같이 정리할 수 있다. 우선, 일반적으로 SSM에서 으로 간소화 하기 때문에 로 표현한다.

실제로 논문에서도 D를 제외한 것을 볼 수 있다.
오른쪽 식의 양변에 를 곱하면 가 된다. 와 동치인 것을 알 수 있다. 동일한 시스템이지만 상태 에서 만큼 기준이 변경되었다고 한다.
이 시스템에서 행렬에 해당되는 대각행렬을 구축할 수 있다면, 앞에서 설명했던 convolution연산의 연산량을 효과적으로 줄일 수 있다. 이것을 Vandermonde product라 한다.
하지만 HiPPO행렬에 대한 대각화는 불가능하다고 한다.
HiPPO 행렬이 대각화되면서 고유벡터로 이뤄진 matrix 가 매우 커지기 때문임.
컴퓨터 상에서 계산이 안정적이기 위해서는 행렬 연산 과정에서 행렬요소가 너무 큰 값을 가지면 안되기 때문에 불가능한 것이다.
그렇기 때문에 논문의 저자는 matrix를 normal matrix + Low rank matrix로 바꿔서 생각해본다.
Normal + Low Rank matrix
matrix를 diagonal matrix로 만들기 위해 추가작업이 필요함을 알 수 있다.
가장 이상적인 조건은 대각화가 가능한 경우이다. 이 조건을 만족하는 matrix의 모음을 normal matrices라고 한다.
저자는 HiPPO matrix 가 normal matrix는 아니지만, Normal + Low Rank matrix로 나타낼 수 있다는 것을 발견하였다. 하지만 여기서 문제는 Convolution 연산에서 합에 대한(Normal + Low)제곱 연산이 필요한데, 이 역시 시간이 오래걸려 최적화가 필요하다.
논문에서는 이 문제를 해결하기 위해 세 가지 알고리즘을 추가로 적용하여 kernel filter를 계산하게 된다.
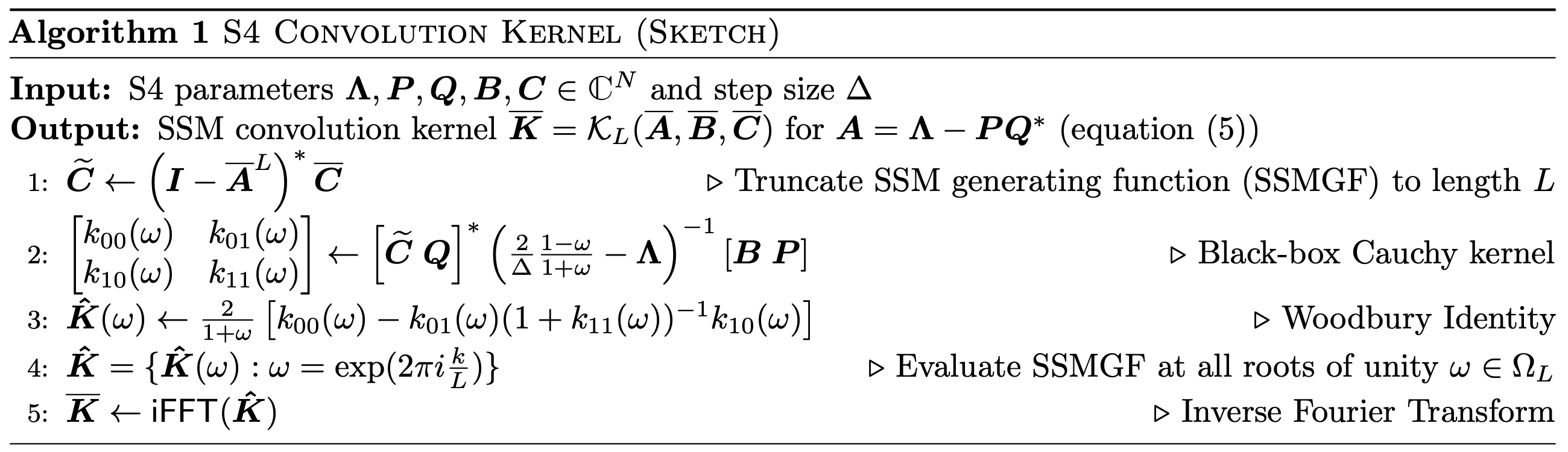
이 알고리즘을 이해하기 위해서는 행렬 가 NPLR(Normal + Low-rank), DPLR(Diagonal + Low-rank)로 나타낼 수 있다는 것을 알고 넘어가야 한다. 이 부분은 아래에서 설명할 것이니 그렇다고 생각하면 된다.
그런 다음, 기존 Convolution kernel을 계산하던 방식에서 차이를 두는데 를 직접 계산하지 않고 의 Discrete Fourier Transformation(DFT)변환 상태인 를 사용한다.
DFT?
DFT는 이산화된 시간 축에서 신호를 이산화된 주파수 축의 스펙트럼으로 바꿔주는 변환에 해당되고, DFT 변환 및 이의 역 변환 IDFT알고리즘은 Fast Fourier Transform(FFT)라고 하며 연산 속도는 에서 해결가능하다.
작동 순서는 다음과 같다.
-
모든 HiPPO행렬 를 NPLR(DPLR)로 표현이 가능하고, 이를 적용하여 (Discretize)를 연산으로 줄일 수 있다.
-
의 truncate SSM generating function은 DFT랑 동일하다. 따라서 주파수 축으로 변환, 역변환을 통해 연산이 가능하며, 이때 의 반복된 제곱 연산 대신 단일 연산으로 바꿀 수 있다.
-
위의 연산과정이 Cauchy Kernel 연산 구조와 동일하기 때문에 효율적인 알고리즘 적용이 가능하다.
-
이때 inverse는 Woobury's identity를 사용하면 간소화 할 수 있다.
매우 복잡하다... 자세한 설명을 시작해보겠다.
자세한 설명
HiPPO 행렬은 NPLR(Normal Plus Low-Rank)로 표현이 가능하다고 말했다.
HiPPO Legs에 대해서 살펴보자.

논문에서 HiPPO-Legs의 matrix 에 대해서 다음과 같이 표현한다. 우리는 이 matrix 에 대해 를 더해줄 것이다. 계산 후 아래의 수식과 같아지는 것을 확인 할 수 있다. (앞에 -가 있다는 것을 확인하길 바란다. 이걸 못봐서 한참동안 보고있었다..)
덧셈을 계산한 후, 대각 성분이 모두 라는 것을 확인 할 수 있다.
따라서 대각성분을 로 분리가 가능해진다. matrix 에서 대각성분을 분리한 matrix를 라고 하면
.
가 된다.
이때 는 우리가 원하는 normal matrix에 속하는 skew-symmetric matrix가 된다.
의문점?
NPLR으로 나타낼 수 있다고 했는데 skew-symmetric matrix가 Low-rank인지는 잘 모르겠다. (rank가 n이라고 생각한다.)
나의 생각:
NPLR과 DPLR로 나타낼 수 있다고 했는데 D가 이고 N이 S라고 생각한다. 그리고 Low-rank는 더해주었던 matrix라고 생각한다. (모두 같은 값이기 때문에 rank가 1) 그렇기 때문에 NPLR, DPLR모두 언급한 것 같음.

여기서 NPLR이 DPLR로 나타낼 수 있다고 나와 있었다.
Computing the S4 Recurrent View
라고 하자.
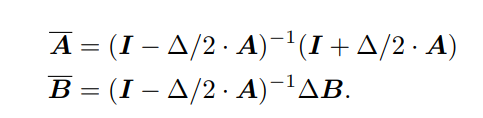
이전에 LSSL논문에서 GBT(Generalized Bilinear Transform)를 통해 A, B를 이산화한 모양이다.

를 계산하는 것은 크게 문제가 없지만 연산에는 큰 문제가 있는데, 바로 역행렬 연산이다. 행렬 차원 수 N이 증가할수록 연산량이 기하급수적으로 늘어난다 . 따라서 역행렬 연산을 DPLR 행렬에 대해 위와 같이 Woodbury’s Identity를 통해 단순화할 수 있다. 대각화된 행렬에 대한 inverse는 쉽게 구할 수 있으며, 뒤에 붙는 low-rank term에는 무관하게 연산이 가능하므로 전체 계산식에 대한 역행렬 연산보다 단순화할 수 있다는 것이다. Woodbury’s Identity의 경우에는 앞으로 전개될 증명 과정에 계속 활용되기 때문에 계속 인지하고 있는 편이 용이하다 (DPLR 구조의 행렬만 가지면 계속 효율적으로 적용이 가능).
Woodbury's Identity
.
Woodbury's Identity는 교환법칙이 성립하는 행렬에 대해서 위의 수식이 성립한다는 것이다.
이때 양 변에 를 곱해주면 identity matrix가 만들어진다.
구한 수식으로 discrete system의 수식을 다시 써보면 다음과 같이 쓸 수 있다.

모두 DPLR로 변환 가능하기 때문에 matrix 곱셈연산은 의 시간이 걸린다고 한다
Computing the Convolutional View
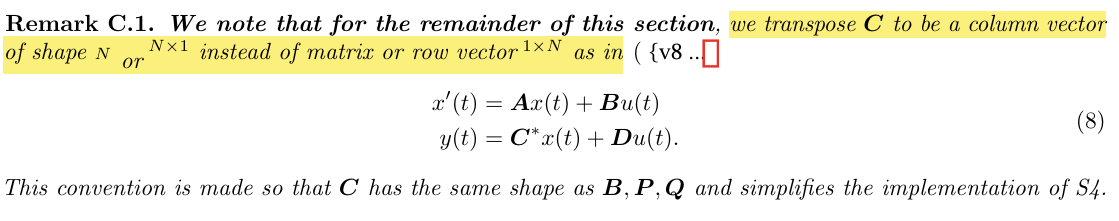
저자는 row vector였던 를 colum vector로 간주하여 와 shape을 맞추었다고 한다.
우리가 구한 discrete system에 DPLR 행렬 을 대입해보면
.
위의 식이 완성되게 된다.
이제 이산화된 시스템의 행렬은 정의가 되었고 recurrent system에서 convolution filter 를 빠르게 연산하는 방법이 필요하다. Woodbury identity를 사용해서 효율성을 높일 수 있다는 것은 알겠으나 convolution연산의 반복곱 연산에는 쓸 수가 없기 때문에 저자는 DFT(Discrete Fourier Transform)을 활용한다.
L의 길이를 가진 한정된 길이의 필터를 생각해보자.
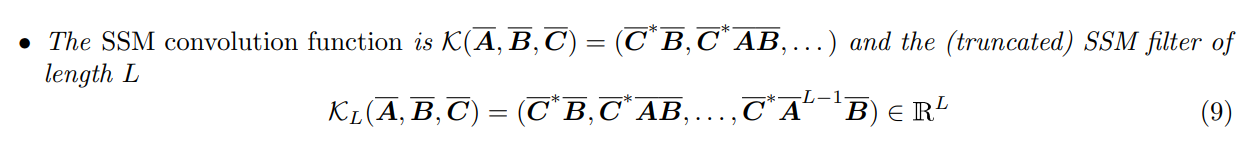
길이가 인 주파수는 의 성분으로 분해가 가능하다. 이 주파수를 표현하는 unit을 라는 변수로 표현을 하면, 위의 식을 함수에 대한 coefficient의 집합으로 대체가 가능해지고 이를 이라고 부른다. 이때 일반적으로 는 복소수 단위를 의미하며 주파수 단위에서는 이를 오릴러 각도 변환식인 에서 의 합으로 표현 가능하다.

여기서 맨 앞의 로 두게 되면
이 수식으로 표현이 가능하게 되고
를 위의 수식에 대입하면
여기에 DPLR로 분해한 A matrix를 넣으면 다음과 같다.
여기서 식을 간소화하기 위해 다음과 같이 두게 된다면
최종 식은 다음과 같게 된다.
이후 여기에 Woodbury identity를 적용하여 수식의 효율을 올리는 것이다.
근데 너무나도 어려운 것이다..

S4 매개변수화에서 을 지속적으로 계산하는 대신, 매개변수를 간단히 재매개변수화하여 C 대신 를 직접 학습할 수 있으며, 이를 통해 사소한 계산 비용을 절약하고 알고리즘을 단순화할 수 있다고 합니다.
왜 그럴까...? 아직까지 근본적인 이해가 가지 않는 부분이다.

마지막으로 이 수식이 Cauchy kernel문제와 동일하기 때문에 효율적으로 계산을 할 수 있다고 한다.
길이 의 convolution kernel을 계산하기 위해서는 만큼의 연산량이 소모되는데, 약간의 오차를 허용한다면 이를 의 연산량으로 처리 가능하다고 한다.
D Experiment Details and Full Results
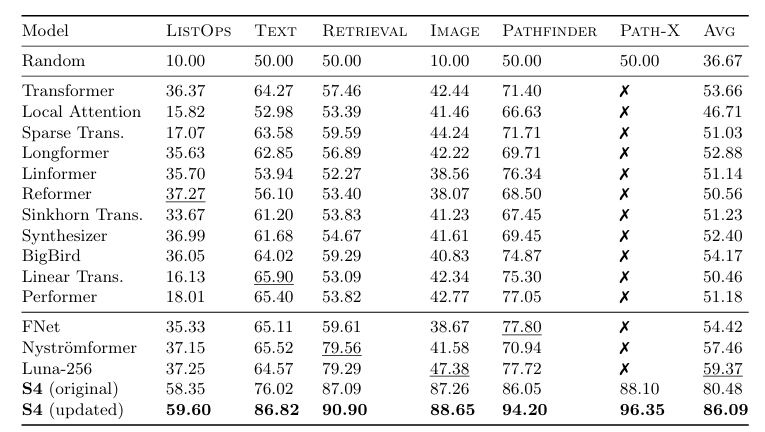
거의 모든 모델보다 Long Range Arena에서 좋은 성능을 보이고 있다.
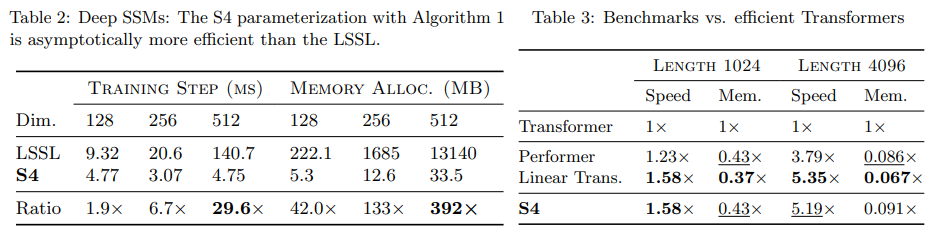
기존 모델과 비교했을 때, 속도가 많이 향상 된 것을 볼 수 있다.
