HiPPO: Recurrent Memory with Optimal Polynomial Projections(2020)

오늘은 Mamba를 읽기 위해 거쳐야 할 논문인 Hippo를 읽어보려고 한다.

논문 링크

---

Introduction

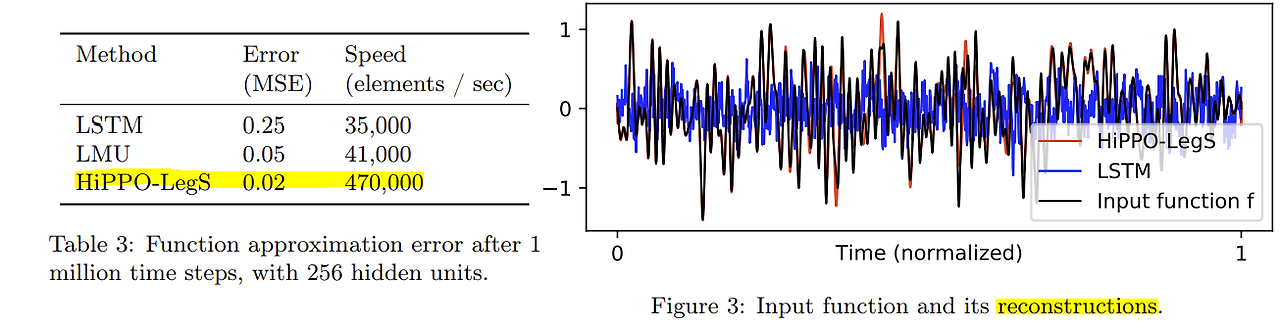
HiPPO 논문은 시계열 모델링을 어떻게 하면 효과적으로 할 수 있을지에 대해 소개하는 논문이다. HiPPO는 long-term sequence modeling 방법이다. LSTM, GRU등의 RNN과 비슷하지만 장기억을 저장하고 복원하는 성능이 더 뛰어나다. HiPPO는 다항식을 사용해 원본의 그래프를 효과적으로 압축하고 복원하는 방식을 사용하여 모델의 기억력을 높인다.

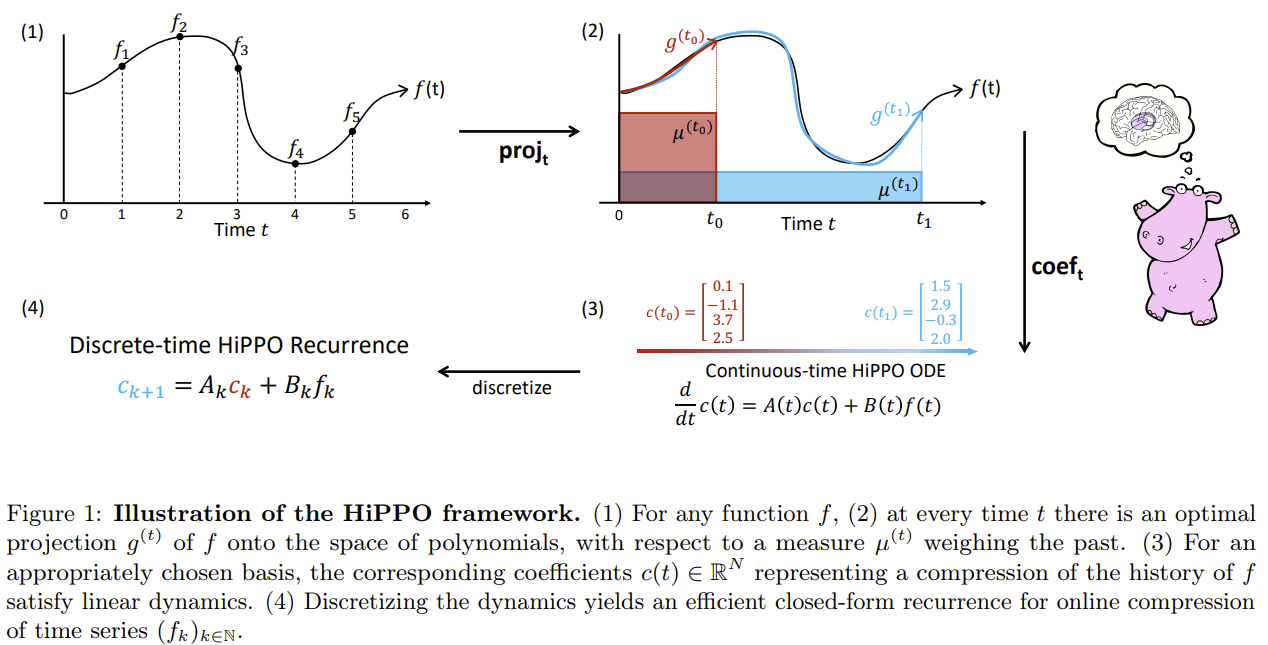
HiPPO 논문에서는 원본 함수를 나타낼 수 있는 orthogonal basis에 원본 함수를 Projection하여 원본함수를 근사하고 내적을 사용해서 orthogonal basis를 형성하는 벡터들의 조합으로 나타낸다. 그리고 이 조합의 계수에 대해 SSM(State Space Model)을 사용해서 다음 계수를 알아낸다.

논문의 내용만을 읽어서는 절대 이해할 수 없는 논문이다. appendix를 자세하게 읽어야 논문에서 말하는 방식을 이해할 수 있다.

47페이지 중 34페이지가 appendix이니 그럴만도 하다..

기존 방식의 문제점

기존의 LSTM, GRU등의 시계열 방법은 모델에게 기억을 관장하는 회로를 추가하여 모델이 기억할 수 있도록 만들었다. 하지만 이 방식은 많이 알려진 vanishing gradient라는 문제가 있다. 기억함수를 0~1의 값에 매핑시키기 위해 tanh, sigmoid를 사용하기 때문에 치역이 0~1로 제한되어 모델의 output에서 멀어질수록 weight update가 잘 되지 않는 것이다.

모든 문제는 gradient descent에서 시작된다. $x$를 처음부터 끝까지 다 봐야 gradient를 얻을 수 있고 파라미터를 업데이트 할 수 있다. 만약 매 순간 최적의 해를 얻을 수 있다면 어떻게 될까?

1. 지금까지 봐왔던 내용을 정보의 손실을 optimal하게 요약할 수 있고
2. 실시간으로 optimal하게 유지할 수 있다면

기억을 더 효과적으로 할 수 있을 것이다. HiPPO는 1을 위해 clased-form solution을 선형대수를 사용하여 구할 수 있는 다항 함수 회귀를 사용했고, 2를 푸는 방법을 소개하는 내용이다.

HiPPO?

HiPPO는 시간에 따른 $x$의 중요도인 $\mu^{t}$를 설정하면 그에 따른 최적의 다항함수 계수인 $c(t)$를 효율적으로 구하고, $c(t)$의 시간에 따른 변화량을 이산적으로 표현할 수 있는 선형변환의 행렬 $A_k$를 구하는 방법이다.
$\mu^{t}$를 설정하는 방식은 여러개가 있다.

• $\mu^{t}(x)$ = $\frac{1}{t}$, $x<t$: 얼마나 오래되었는지는 상관없이 모든 부분을 중요하게 보는 것(HiPPO의 A행렬)

• $\mu^{t}(x)$ = $\exp^{x-t}$, $x\leq t$: GRU

기존 RNN 모델들이 HiPPO의 다른 버전임을 보여준다.

Online Function Approximation

Online function approximation은 매 time step $t$마다 함수 $f$의 $x \leq t$ 부분을 기억하는 것을 목표로 한다. 그리고 정의역이 $x \leq t$로 제한된 함수를 $f_{x\leq t}$로 표현한다.

HiPPO는 $f_{x\leq t}$를 고차 다항함수의 합으로 표현하고자 한다. $x \leq t$를N-1차 다항함수를 N개 $p^{(t)}_0, p^{(t)}_1, ..., p^{(t)}_N$를 미리 정의한 후, 이 함수들을 조합하여 $x \leq t$를 근사한다. 그리고 이 선형 결합의 계수 $c_n(t)$를 구한다. 이를
.

$f_{\leq t}$ $\approx$ $\sum\limits_{n=0}^{N-1}{c_n(t)p_n^{(t)}}$

와 같이 표현할 수 있다. 따라서 Hippo는 임의의 함수 $f$를 고차 다항함수(High-order Polynomial)로 재표현(projection)하는 연산자(Operators)를 말한다.

Contributions

1. 장기 기억모델 HiPPO: 기존 RNN, GRU, LSTM등의 시계열 모델 연구의 핵심은 explicit한 기억과 망각이다. 기억과 망각회로를 직접 집어넣어 모델이 특정 부분을 얼마나 기억할지, 잊어버릴지를 결정하도록 한다. 한편 다항함수는 계수 N개만으로 함수 전체를 복원할 수 있다. 따라서 유한개의 스칼라로 거의 완벽한 암기를 할 수 있는 것이다. 기억을 관장하는 부분을 HiPPO로 바꿔 끼움으로서 시간거리가 먼 곳도 참조할 수 있게된다.

2. 실시간문제를 빠르게 푸는 법 제시: K개의 점이 주어졌을 때, N차 다항회귀 방법의 시간복잡도는 $O(K * N^2 + N^3)$이라고 한다. 역함수의 연산에 따라 달라지긴 하지만 $K$는 매우 크다. 따라서 함수 차원 N은 많은 제약을 받는다. 하지만 HiPPO는 이전의 결과값을 재활용하여 빠르게 푸는 방법을 제시한다. 따라서 N에 대한 제약을 덜 받아 큰 값을 가져갈 수 있다.

3. HiPPO가 LSTM, GRU등의 generalization임을 수학적으로 보임: 특정한 다항함수의 집합을 활용하면 LSTM, GRU를 도출할 수 있다.

4. HiPPO의 특징 발굴: 2번을 포함하여 시간스케일에 영향을 받지 않음, RNN에 삽입되면 vanishing gradient 문제 해결가능

이 글의 목표

나는 처음에 수학적인 내용을 제외한 상태로 글을 읽었다. 그래서 처음에 읽을때 근본적인 이해가 되지 않았다. 그래서 HiPPO-LegS를 중심으로 수식에 대해 처음부터 정리했다.

• $\mu$가 뭐지?
• 어떻게 시간에 대해 invariant할 수 있을까?
• A가 왜 저렇게 나오는거지?
• GBT?
• SSM?
• 라게르, 르장드르 다항함수 등

나는 이 글에서 논문을 읽으면서 의문이 들었던 내용 위주로 지식을 공유하고자 한다.

HiPPO는 크게 3부분으로 나눌 수 있다.
$proj_t$, $coef_t$, discretize
시간에 따른 계수들의 변화를 SSM을 이용해 재활용하는 구조이다.

---

SSM: State-Space Model

State Space Model(상태 공간 모델)은 동적 시스템을 수학적으로 나타내는 대표적인 방식입니다. 이를 통해 시스템의 상태, 입력, 출력 간의 관계를 선형 대수의 형태로 표현할 수 있습니다. 특히, 선형 시불변 시스템(LTI: Linear Time-Invariant System)을 수식적으로 나타내기 위해 널리 사용되며, 시스템의 동적인 성질을 정확하게 파악할 수 있습니다.

State Space Model은 두 가지 방정식(상태방정식/출력방정식)으로 표현됩니다:

상태 방정식(State Equation):

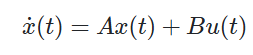
출력 방정식(Output Equation):

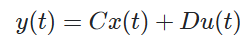
여기서:

• x(t)는 시간 t에서의 상태 벡터입니다.
• $x˙(t)$는 상태 벡터의 변화율(미분)입니다.
• u(t)는 입력 벡터로 시스템에 주어지는 외부 신호입니다.
• A,B,C,D는 시스템의 특성을 나타내는 행렬입니다.

💡여기서 잠깐!
State Space Model의 상태 방정식이 상미분방정식(ODE)의 형태로 표현되어있는 것을 확인할 수 있습니다. 이는 시스템의 상태 변화율을 의미하며, 이를 통해 시스템의 상태가 어떻게 시간에 따라 변하는지(동적인 성질)를 분석할 수 있습니다.

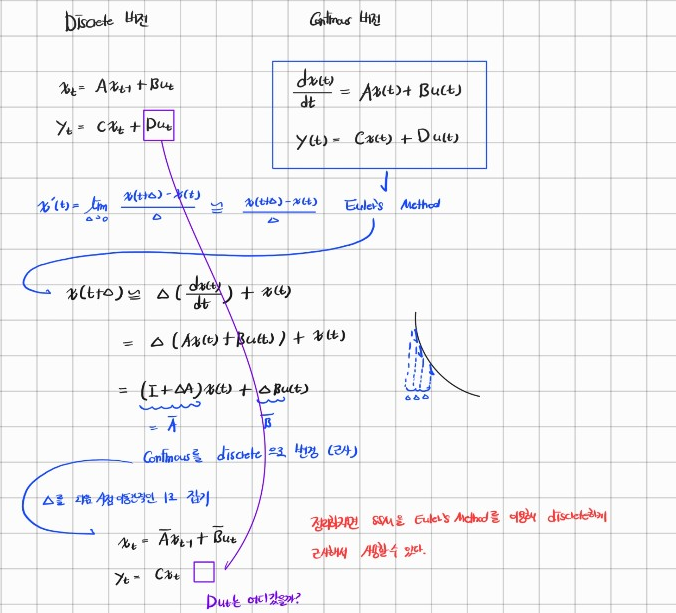
State Space Model(상태 공간 모델)은 시스템의 상태를 연속적인 시간에 따라 변화하는 방식으로 설명합니다. 하지만 실제로는 대부분의 컴퓨터나 디지털 제어 시스템은 연속적인 시간을 직접 처리할 수 없기 때문에, 이 모델을 이산화(Discretization) 과정으로 변환할 필요가 있습니다. 이산화는 연속적인 시간 축에서 발생하는 변화를 이산적인 시간 간격으로 나누어 분석하고 계산하는 과정입니다.

Continuous 시간에서 Discrete 시간으로 변경

이산화 방법 중 가장 기본적이고 많이 사용되는 방법이 오일러 방법(Euler Method) 입니다. 오일러 방법은 연속적인 미분방정식의 변화를 작은 시간 간격 Δt로 나누어, 각 시간 구간에서의 상태 변화를 근사합니다.

근사하는 과정은 다음과 같습니다.

Measure와 함수 간 내적

우리는 함수 $f_{\leq t}$의 가장 비슷한 다항함수의 projection인 $g^{t}$를 구하고 싶다. 여기서 우리는 비슷한을 정의하기 위해 거리개념이 필요하다. 함수를 벡터의 연장으로 생각해서 RMSE를 거리로 두면 되지 않을까? 하는 생각이 드는데 어느정도 맞는 말이다.

$[0,∞)$에서 정의된 실함수 $f, g$가 square integrable이라면 내적 $⟨f, g⟩_{L_2}$ = $\int^∞_0 f(x)g(x)dx$는 힐베르트 공간을 형성할 수 있고, $f$의 norm은 $||f||_{L_2}$ = $⟨f, f⟩^{\frac{1}{2}}_{L_2}$와 같다.

💡 힐베르트 공간?
힐베르트 공간은 내적이 정의된 공간이다. 내적을 정의하면 이 공간안에 있는 원소간의 구조를 알 수 있다.
힐베르트 공간을 이루는 원소인 벡터는 크기가 유한해야 한다. 무한히 크면 안된다.

💡 실함수?
실수의 어떤 집합의 각 요소 속에, 각각 하나의 실수를 대응시키는 것과 같은 함수. 즉, 그 정의역도, 치역도 실수만으로 성립되어 있는 것과 같은 함수.

💡 왜 내적을 적분으로 표현했을까?
함수를 벡터에 대응시켜 내적을 정의하기 위해 -> 함수를 힐베르트 공간의 원소로 표현가능함.

기본 아이디어
1. n차원 벡터를 만들기 위해 함수의 정의역을 n등분한다.
2. n번째 구간의 대표값을 n번째 원소로 하는 벡터를 생각한다.
3. 벡터를 내적한 값이 수렴하도록 각 항에 구간의 크기를 곱한다.
4. n값을 무한으로 보내면, 내적한 값을 적분 값으로 수렴한다.

여기서 square integrable은 적분 $\int^∞_0 |f(x)|^2dx$가 발산하지 않는다는 뜻이고, 힐베르트 공간은 함수들의 집합이 되는데 이 공간의 함수들은 내적값이 크면 비슷하게 생겼다는 것을 알 수 있다. ( 거리는 $||f-g||_{L_2}$로 정의함 )

한편, 우리는 함수를 다항함수로 표현하고 싶다. 만약 다항함수들이 orthogonal basis를 형성한다면 예쁘게 표현이 가능하다.

내적으로 다항함수 조합의 계수를 구하는 방법

$N$차원 벡터 $\mu$를 orthogonal basis $V = {v_0, v_1, ..., v_{N-1}}$이 span하는 선형공간에 projection 시켜보자
.

$u$ $\approx$ $\hat{u}$ $=$ $c'_0v_0 + c'_1v_1 + ... + c'_nv_n + ... + c'_{N-1}v_{N-1}$ = $\sum\limits_{n=0}^{N-1}c'_nv_n$

이를 $\hat{u}$의 basis expansion이라고 한다. 기저가 orthogonal 하다는 것은 임의의 $i, j \in [N]$에 대해 $⟨v_i, v_j⟩ = \delta_{i, j}$라는 뜻이다.
따라서 계수 $c'_n$은 쉽게 구할 수 있다.

$⟨v_i, v_j⟩ = ⟨\sum\limits_{i=0}^{N-1}c'_iv_i, v_n⟩$
$= \sum\limits_{i=0}^{N-1}c'_i⟨v_i, v_n⟩$
$= 0+0+...+c'_n⟨v_n, v_n⟩+...+0$
$= c'_n||v_n||^2$
$=: c_n$

두 값을 내적하면 $v_n$의 basis와 일치하는 성분의 계수만 $c_n$에 포함되기 때문에 $v_n$으로 형성된 힐베르트 공간상에 함수의 원형을 projection할 수 있는 것이다.

우리는 이제 내적이 잘 정의되었다면 N개의 orthogonal한 다항함수 기저로 함수를 정의할 수 있다는 사실을 알게되었다.

임의의 두 다항함수를 곱해서 적분했을 때 0이 나오는 다항함수 집합을 찾으면 된다. 조금 어렵지만 이미 정의된 유명한 orthogonal한 다항함수 기저들이 많다. 라게르, 르장드르 다항함수가 그 예이다. 정확히는 내적을 위와같이 정의하면 안 되고 적절한 weight function $w(x)$를 같이 주어야 수직이 된다.

적절한 $w(x)$를 같이 줬다는 표현을 $d\mu(x)$로 표현한다.

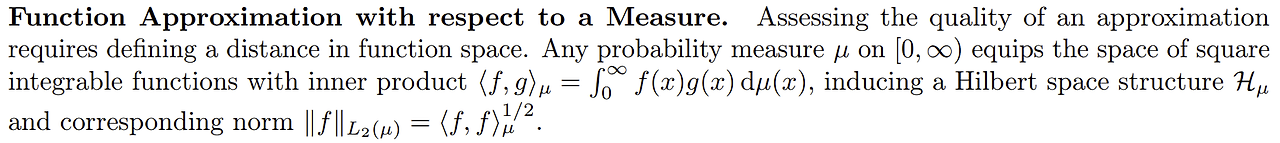
• 적절한 weight function을 주는 $\mu$를 measure라고 한다.

💡 measure를 맘대로 정의할 수 있을까?
안된다. 선택한 다항함수의 basis를 orthgonal하게 만들어 주는 weight를 선택해야함.
ex) 라게르의 경우 $w(x) = x^{\alpha}\exp^{-x}, x \geq 0$을 줘야 다항함수 basis가 orthogonal 하게된다.
르장드르의 경우 $w(x) = \frac{1}{2}$이다. 특별한 measure없이 orthogonal임.

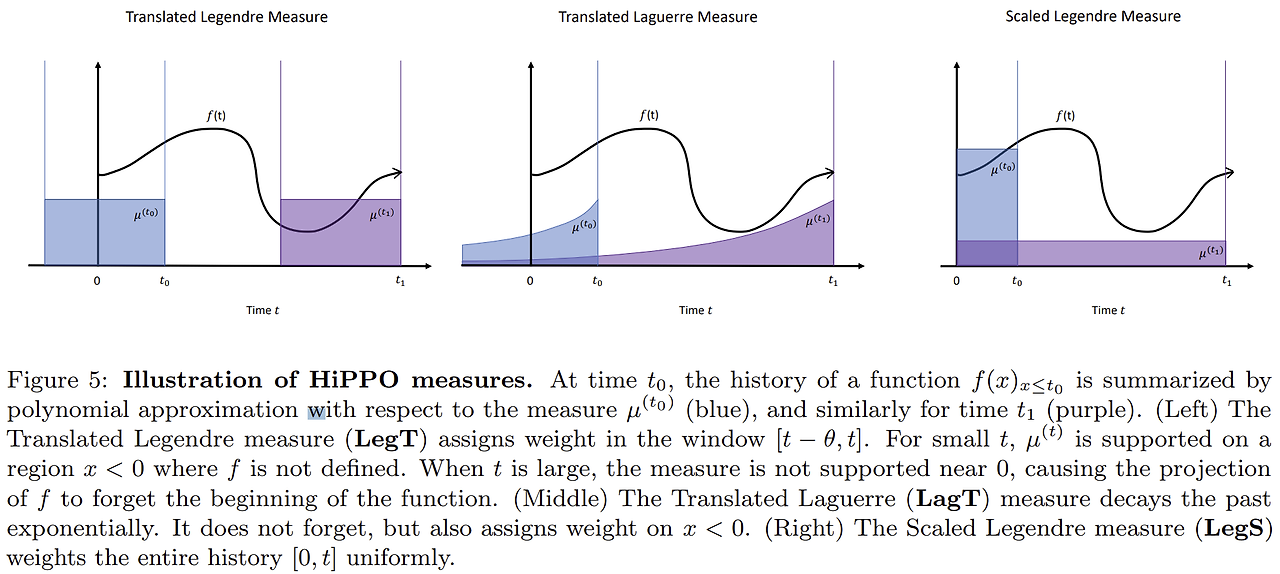
HiPPO에서는 이렇게 정해진 $\mu$를 시간에 따른 중요도로 해석했다. 라게르 weight function에서 $\alpha = 0$으로 주면 $w(x) = \exp^{-x}$가 된다. HiPPO에서는 이를 뒤집어서 $\exp^{(t-x)}, x \leq t$로 만들었다.
x가 t에서 멀어질수록 weight값이 작아짐 -> 오래될수록 덜 중요함

---

$proj_t$와 $coef_t$ 계수들의 Dynamics

우리는 $f_{\leq t}$를 다항함수 $g^{(t)}$에 projection하고 있다.
($g^{(t)}$는 다항함수의 기저 ${g_n}_{n \leq t}$가 span하는 공간의 한 원소임)
$g^{(t)}$의 basis expansion의 계수 $c_n(t)$는 내적으로 쉽게 구할 수 있음.
.

$f_{\leq t} \approx g^{(t)}$
$c_n(t) := ⟨f_{\leq t}, g_n⟩_{\mu(t)}$

• $f_{\leq t} \approx g^{(t)}$ $proj_t$ 연산
• $c_n(t) := ⟨f_{\leq t}, g_n⟩_{\mu(t)}$ $coef_t$ 연산

구한 계수 $c_n(t)$를 재활용하기 위해 (= 시간 복잡도를 줄이기 위해) 계수들의 dynamics를 활용할 수 있다. Dynamics는 SSM을 구하면 쉽게 알 수 있다. SSM을 구하귀 위해 ODE를 closed-form으로 구해야 한다.$c_n(t)$의 정의로부터 closed-form ODE를 얻으려면 어떻게 해야할까? 우리가 구해야 하는 form은 다음과 같다.

.

$c'_n(t)$ = [function of $c_n(t)$ and $t$]

💡 ODE?
구하려는 함수가 하나의 독립 변수만을 가지고 있는 미분 방정식이다.
Euler's method를 통해 다음 계수값을 구하는 것이 최종 목적임. -> 미분 방정식필요

함수간 내적은 적분으로 정의가 된다. $c'(t)$의 정의를 미분하면 좌변은 우리가 원하는 항이 되고 우변은 계산을 좀 더 하면 $cn(t), c{n-1}(t), ...으로 표현할 수 있다. 이 부분은 계산이 복잡해서 appendix에서 확인할 수 있다.

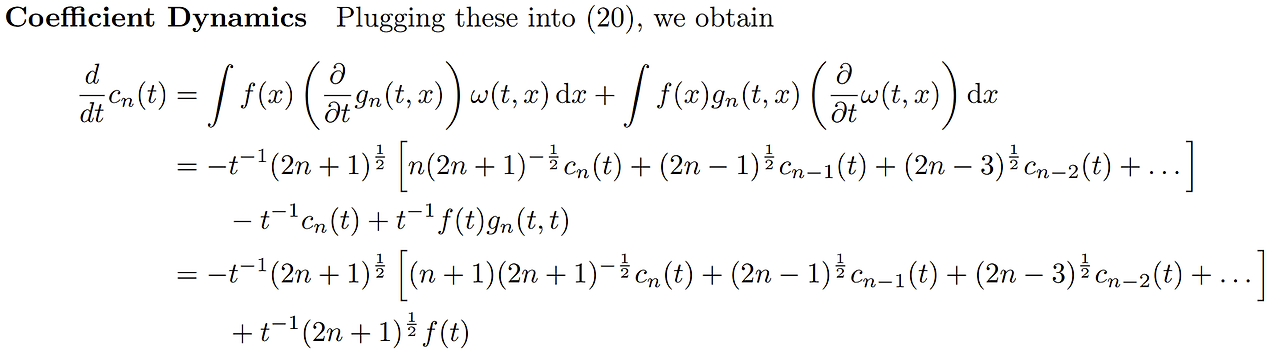
appendix 증명을 아래에서 자세하게 살펴보겠다.

$hippo(f)$는 $proj_t$의 결과를 $coef_t$하여 $f_{\leq t}$를 projection한 다항함수의 선형결합 $g^{(t)}$의 계수를 구하는 함수이다. $hippo(f)$의 결과는 projection 함수의 basis expension계수인 N개의 스칼라이다. 그리고 이 계수는 매 시간마다 바뀐다. 왜냐 시간이 달라질때마다 weight function의 값이 달라지기 때문이다.

이제부터 Appendix를 살펴볼 것이다.

---

Appendix

Appendix C, D

Appendix C는 $f$로 부터 $c$를 얻는 과정을 general하게 설명하고, D는 scaled and shifted 르장드르 다항함수 기저와 measure를 대입해서 직접 계산한다. D에서는 LegS말고도 여러 basis-measure 세트에서 계산을 했지만 나는 LegS만 살펴봤다.

Appendix C는 문제 정의부터 시작한다. ($(-∞, t]$에서 정의된 time vaying measure $\mu^{(t)}$, 기저 함수의 수열이 만드는 공간 $G = span{g_n^{(t)}}_{n \in [N]}$와 연속함수 $f:\mathbb{R}_{\geq 0} \rightarrow \mathbb{R}$ 가 주어졌을 때, HiPPO는 $f$로부터 다음을 만족하는 $f$의 optimal projection의 계수 $c:\mathbb{R}_{\geq 0} \rightarrow \mathbb{R}^N$을 얻는 연산자로 정의한다.

.

$g^{(t)} := argmin_{g \in G}||f_{\leq t} - g||_{\mu^{(t)}}$, and $g^{(t)} = \sum\limits_{n=0}^{N-1}c_n(t)g_n^{(t)}$

HiPPO라는 함수에 $f$를 넣으면 $c$가 나온다는 것을 알 수 있다.
우리는 이로부터 ODE $\frac{d}{dt}c(t) = Ac(t) + Bf(t), \in \mathbb{R}^{N \times N}, B \in \mathbb{R}^{N\times 1}$을 얻을 것이다.

정의들

시간에 따른 중요도인 measure $\mu$가 주어졌을 때 ${P_n}_{n \in \mathbb{N}}$은 $\mu$에 대해 orthogonal한 다항함수 기저로 정의한다.
$⟨P_i, P_j⟩_\mu = \delta_{ij}, i,j \in \mathbb{N}$ 논문에서는 $⟨P_i, P_j⟩_\mu = \delta_{ij}$라고 써놔서 처음에는 $\mu$가 주어졌을때 이들이 orthogonal하게 된다고 받아들였다. 하지만 라게르, 르장드르 같은 기존에 있는 다항함수 basis를 먼저 선택하고 이들을 orthogonal하게 만드는 $\mu$를 찾는 것이었다.

실시간 다항회귀에서는 실시간으로 정의역이 변한다. 시점 $t$에서 $[0, t)$임.
$\mu$는 정의역 전체를 나타내기 때문에 $\mu$도 같이 변한다. 이를 $\mu^{(t)}$로 표기한다. 다항함수는 measure와 세트라 같이 변한다. (함수의 형태가 변하는 것은 아님 scaling and shifting 정도) 이를 ${P_n^{(t)}}_{n \in \mathbb{N}}$으로 표기한다.

$p_n^{(t)}$는 $P_n^{(t)}$의 normalized 버전임. Norm이 1이 되도록 norm으로 나눠준 값임.

💡 왜 normalized?
계수와 basis인 $P_n$을 내적하면 $f_{\leq t}$가 나와야 하기 때문임
normalized를 하지 않으면 적분값을 그대로 쓰기 때문에 $f_{\leq t}$가 나오지 않음.

여기에 tilting이라고 다항함수를 orthogonal로 만들어주기위한 장치가 하나 더 있는데 르장드르는 필요 없기 때문에 정의는 생략한다. 다만, 계속 등장하기 때문에 르장드르에서는 $X=1, ζ=1, g_n=p_n, v=\mu$라고 생각해서 대입하면 된다.

그리고 $\omega(t, x) = \omega^{(t)}(x)는 \mu$가 주는 중요도 weight function이다.

Projection과 계수

input은 실시간(online)으로 주어지는 $f$의 일부분 $f_{\leq t}(x) = f(x)_{x \leq t}$이다.
$f:[0, ∞) \rightarrow \mathbb{R}$는 1번 이상 미분 가능한 함수이다.

output은 optimal한 projection의 계수이다. orthogonal basis ${p_n}_{n \in [N]}$이 주어졌을 때,

.

$c_n(t) := ⟨f_{\leq t}, g^{(t)}_n⟩_{\mu^{(t)}}$

$= \int fp^{(t)}_n \omega^{(t)}$

$= \int^t_0 f(x) \cdot p^{(t)}_n(x) \cdot \omega^{(t)}(x) dx$

이것이 $c$의 정의이다. 이 개념을 확실히 기억해두고 가야 아래 증명과정이 덜 헷갈린다.

계수를 구했다면 함수를 복원할 수 있다.
.

$f_{\leq t} \approx g^{(t)} := \sum\limits_{n=0}^{N-1}⟨f_{\leq t}, p_n^{(t)}⟩_{\mu^{(t)}}p_n^{(t)} = \sum\limits_{n=0}^{N-1}c_n(t)p_n^{(t)}$
위의 글을 잘 따라왔다면 이제 식이 어느정도 보일 것이다. t시점 이전으로 제한된 input대해서 output이 유한하기 때문에 함수의 output값을 벡터로 만들어 힐베르트 공간의 원소로 표기를 할 수 있는 것이고 그렇게 힐베르트 공간인 르장드르 다항식을 orthogonal basis로 사용하여 다항식의 선형 결합으로 원본 함수를 근사하여 projection하는 것이다. ($p_n^{(t)}$는 normalized한 값이기 때문에 내적을 바로 계수로 쓸 수 있는 것임.)

이렇게 계수를 통해서 우리는 원본함수의 근사값을 복원할 수 있는 것이다.

Coefficient Dynamics

이 내적을 사용해서 ODE를 만들 것이다.

$\frac{d}{dt}c_n(t) = \int f(x)(\frac{\partial}{\partial t}p_n(t, x))\omega(t, x)dx$ + \int f(x)p_n(t, x)(\frac{\partial}{\partial t}\omega(t, x))dx

이 미분은 곱의 미분을 사용한 형태이다. t에 대한 미분에서 $f(x)$는 제외되기 때문임. 첫 번째 항부터 봐보자. 다항함수는 미분을 해도 다항함수이다. 그러면 basis로 다시 나타낼 수 있다. 따라서 $p_0, ..., p_{n-1}$의 선형결합으로 표현할 수 있다. 그러면 $c$로 다시 표현할 수 있다.

두 번째 항은 $\omega$가 미분했을때 이상한 form이 나오면 적분이 그대로 살아있을 것이기 떄문에 여기서 막힌다. 하지만 다항함수 basis로 르장드르를 사용할 경우 $\omega'$도 $\omega$로 표현이 가능하다. 따라서 $c$의 정의에 따라 다시 $c$로 표현이 가능하다.

따라서 ODE가 완성될 수 있는 것이다. 이렇게 구한 ODE는 다음과 같이 표현할 수 있다.
.

$\frac{d}{dt}c(t) = -Ac(t) + Bf(t)$

이것이 바로 hippo 연산자의 실체이다. A앞의 -부호는 계산의ㅡ 편의를 위해 써놓았다.

C. 이산화

$\frac{d}{dt}c(t) = -Ac(t) + Bf(t)$로 부터 Euler's method를 사용해서 $c_k = -Ac_{k-1} + Bf_k$를 얻는다.

D. HiPPO 연산 계산

이제 거의 다왔다. D는 C에서 유도한 식에 각 다항함수의 basis와 measure를 대입니다. 이 글에서는 LegS만 살펴본다. 계산은 크게 4단계로 나눌 수 있다.

1. measure와 basis, 2. 다항함수와 중요도 미분, 3. 계수 동역학, 4. 복원

1. measure와 basis

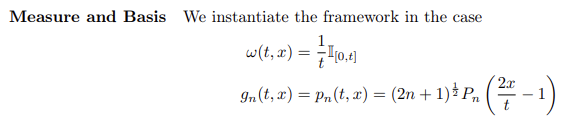
르장드르 다항함수 $P_n$은 $[-1, 1]$에서 정의된다. $[0, t]$에서 사용하려면 위와 같은 scaling을 거쳐야 한다. $(2n+1)^{\frac{1}{2}}$는 $P_n$의 norm이다. $\mathbb{I}$는 rect function이다. ($[0, t]$에서만 1이고 나머지는 전부 0이라는 뜻)

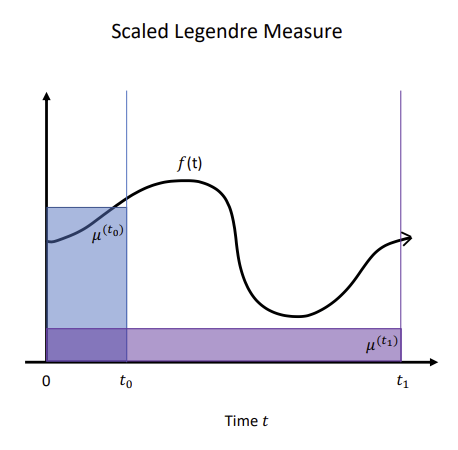
오른쪽 그림의 파란색과 보라색은 서로 다른 $t$에 대한 $\omega$이다.

$\omega$가 $\frac{1}{t}$이기 때문에 t가 클수록 작아지는 형태임.

2. 다항함수와 중요도 미분

위에서 두번째 항의 적분꼴을 없에려면 $\omega'$을 $\omega$로, $g'$은 $g$로 표현하는 것이 핵심이라고 했다. ($c$의 정의를 다시 보고 올것.)

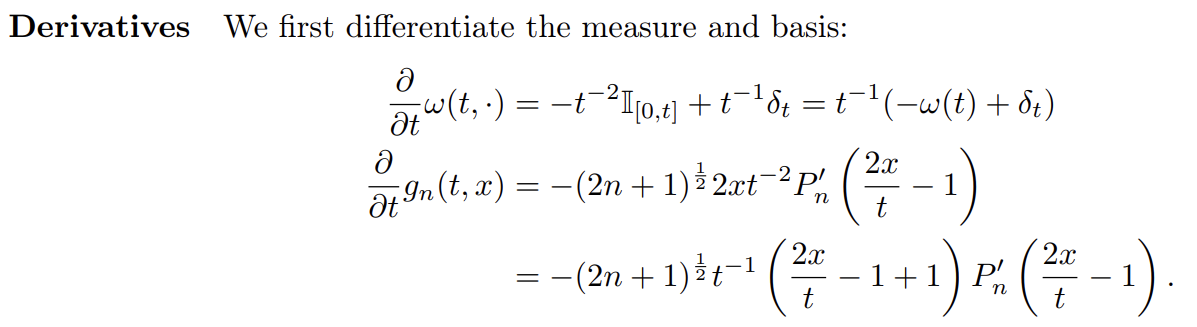
첫번째 항부터 살펴보자.
우리는 $\frac{1}{t}$와 rect function $\mathbb{I}[0, t]$모두 t에 대한 식이기 때문에 미분을 해줘야 한다. (곱의 미분을 해준다.)

💡 direc delta 함수 $\delta$는 어디서 나왔을까?
rect function을 미분하면 direc delta함수가 나온다.

두번째 항을 보자.
이 식에서 구간은 $[0, t]$로 만들기 위해 $z = \frac{2x}{t}-1$로 놓으면 다음과 같은 식이 나온다.

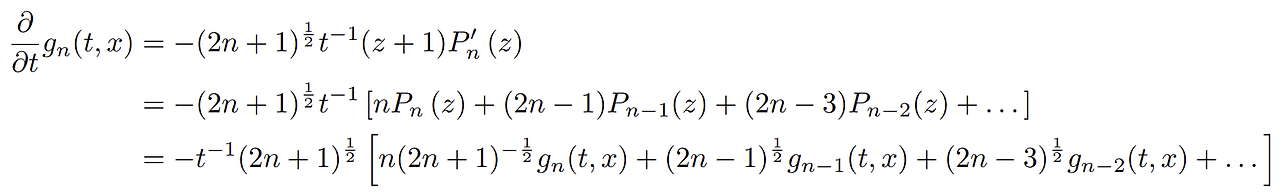
$g_n, g_{n-1}, ...$으로 재표현 되었다.

3. 계수 동역학

C.3에서 만든 식에 2.에서 미분한 식을 대입해보자

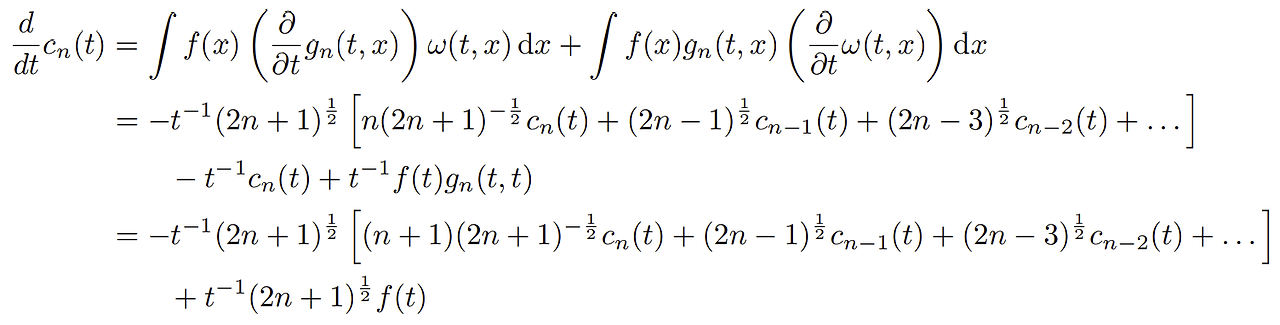
$\frac{1}{t}$로 묶으면 선형결합이기 때문에 다음과 같은 행렬식으로 표현이 가능해진다.

이해하기 어려웠던 부분들

처음에 나는 어떻게 $g_n, g_{n-1}, ...$의 형태에서 $c_n, c_{n-1}, ...$로 넘어가는지 이해가 되지 않았다.

알고보니 위의 식의 $f, \omega$를 같이 곱해서 $g$를 $c$에 대한 식으로 바꿔준 것이었다.

두번째 항에서는 $\frac{\partial}{\partial t}\omega(t, x)$가 특정조건에서 $\omega(t, x)$의 선형 결합형태로 나타날 수 있다.
그런데 르장드르 다항식에서는 그 조건을 충족하기 때문에 다음과 같이 표현이 가능한 것이었다.

행렬식에 대해 어떻게 $c_n(t)$로 묶일 수 있는가?

$\frac{\partial}{\partial t}\omega(t, x) = \beta_n(t)\omega(t, x)$

이 식을 적분에 대입하면 다음과 같은 식이 된다.
.

$\int f(x)p_n(t, x)\frac{\partial}{\partial t}\omega(t, x)dx = \beta_n(t)\int f(x)p_n(t, x)\omega(t, x)dx$

.
여기서 $\int f(x)p_n(t, x)\omega(t, x)dx = c_n(t)$를 대입하면
.

$\int f(x)p_n(t, x)\frac{\partial}{\partial t}\omega(t, x)dx = \beta_n(t)c_n(t)$
.
로 표현이 가능해진다.

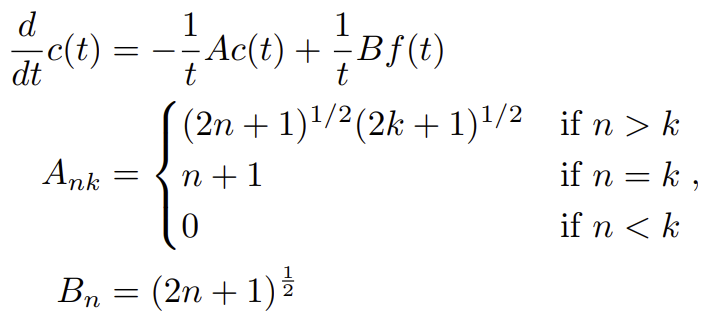
그러면 다음과 같이 행렬식으로 표현이 된다.

이기 $A$가 계속 등장할 HiPPO-LegS A이다. A앞의 -부호에 주의하자.

4. 복원

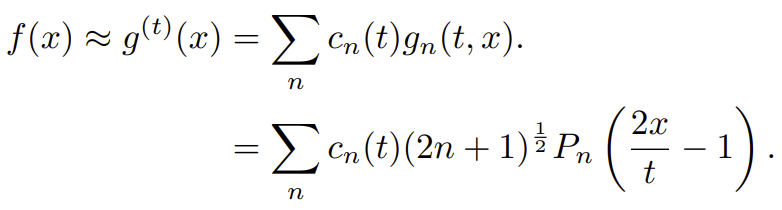
basis $g_n$과 $c_n$을 선형조합하여 복원한다.

이산화

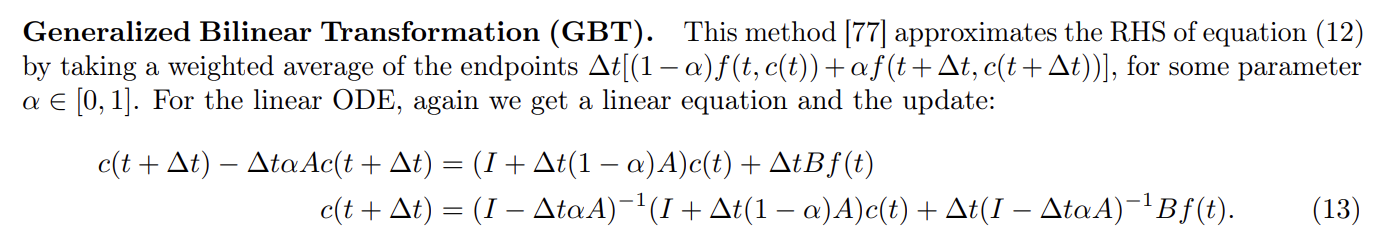
위 GBT 계산 식에 집어넣으면 된다. 미리 계산되어있다.
$t$시점의 값과 기울기의 값을 비율을 조정하여 합하는 방식으로 다음 값을 구한다.

여기서 핵심은 HiPPO-LegS의 이산화는 $\delta t$가 없다는 점이다.
왜 없어졌을까?

$\frac{d}{dt} c(t) = \frac{1}{t} A c(t) + \frac{1}{t} B f(t),$

기본형태이다.

$c(t + \Delta t) - \Delta t \alpha \frac{1}{t + \Delta t} A c(t + \Delta t) = \left( I + \Delta t (1 - \alpha) \frac{1}{t} A \right) c(t) + \Delta t \frac{1}{t} B f(t).$

GBT를 이용한 수식을 정리하면 다음과 같다.

$c(t + \Delta t) = \left( I - \Delta t \frac{\alpha}{t + \Delta t} A \right)^{-1} \left[ \left( I + \Delta t \frac{1 - \alpha}{t} A \right) c(t) + \Delta t \frac{1}{t} B f(t) \right].$

여기서 수식을 다음의 값으로 치환해준다. ($\frac{1}{t} = \frac{1}{k \Delta t}, \quad \frac{1}{t + \Delta t} = \frac{1}{(k+1) \Delta t}.$)

치환된 식을 다음과 같이 변형할 수 있다.

$\Delta t \frac{\alpha}{t + \Delta t} = \frac{\alpha}{k + 1}, \quad \Delta t \frac{1}{t} = \frac{1}{k}.$

이후 수식에 대입해주면 t에 대한 값이 모두 상쇄된다.

$c^{(k+1)} = \left( I - \frac{\alpha}{k+1} A \right)^{-1} \left[ \left( I + \frac{1 - \alpha}{k} A \right) c^{(k)} + \frac{1}{k} B f^{(k)} \right].$

( $c^{(k)} = c(k \Delta t), \quad f^{(k)} = f(k \Delta t).$ 을 만족 )

따라서 HiPPO는 time-scale에 invariant하다.

---

읽으면서 고민을 굉장히 많이 한 논문이다. 수식이 많고 복잡하기 때문에 읽으면서 수학적 지식의 필요성을 느꼈다.

다음 리뷰할 논문은 LSSL이 될 것 같다!