DDPM: Denoising Diffusion Probabilistic Models

Introduction

오늘은 DDPM논문에 대해서 리뷰하려고 한다.

이전 글에서의 VAE(Variational Auto Encoder)의 ELBO수식이 그대로 활용되어 loss수식에 대한 내용은 크게 어렵지 않았다.

하지만 조건부 확률에 대한 수식의 내용을 소개하는 글은 많이 없어, 이번 글의 내용은 Reparameterization Trick기법을 사용한 Sampling과 Sampling된 평균, 분산을 증명하는 내용을 중심으로 포스팅할 예정이다.

논문에서도 해당 부분이 핵심인 것 같다고 생각했다.

자! 포스팅 시작~!

---

DDPM

DDPM은 VAE와 같이 생성형 모델의 대표적인 모델 중 하나이다.

DDPM의 목표도 VAE와 동일하게 input과 다른 이미지 데이터를 생성하는 것이다.

차이점은 그 방식이 약간 다르다는 점이다.

VAE

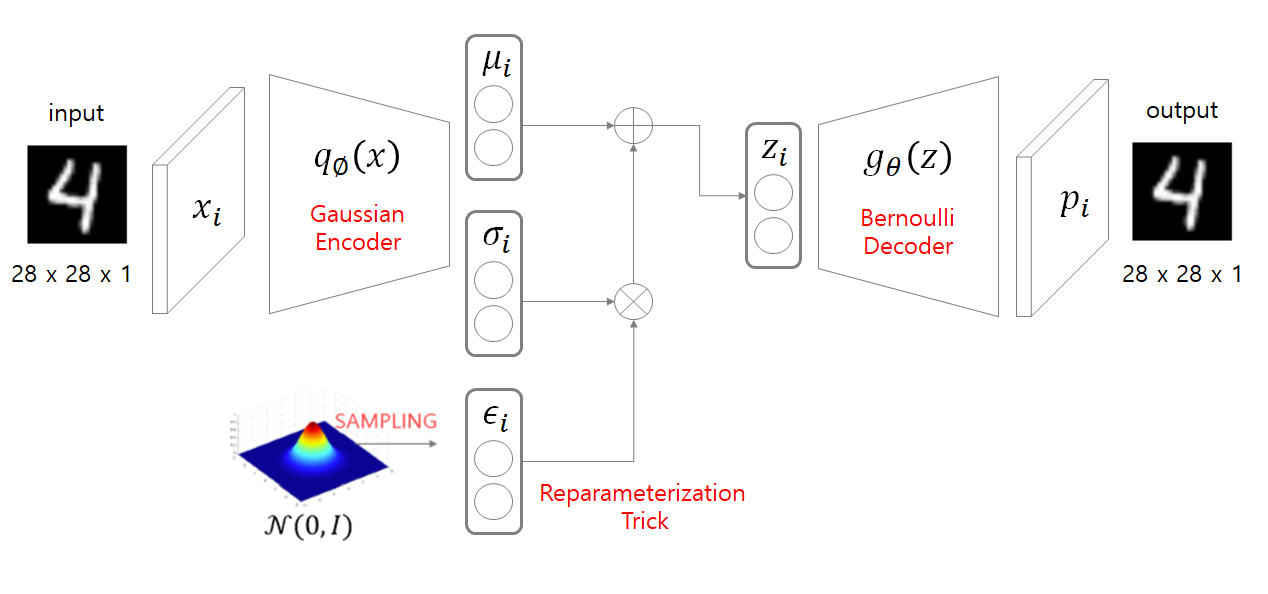
VAE는 Encoder를 통해 latent space z를 만들고 sampling된 z를 Decoder에 넣어 input과 비슷한 이미지를 출력한다.

DDPM

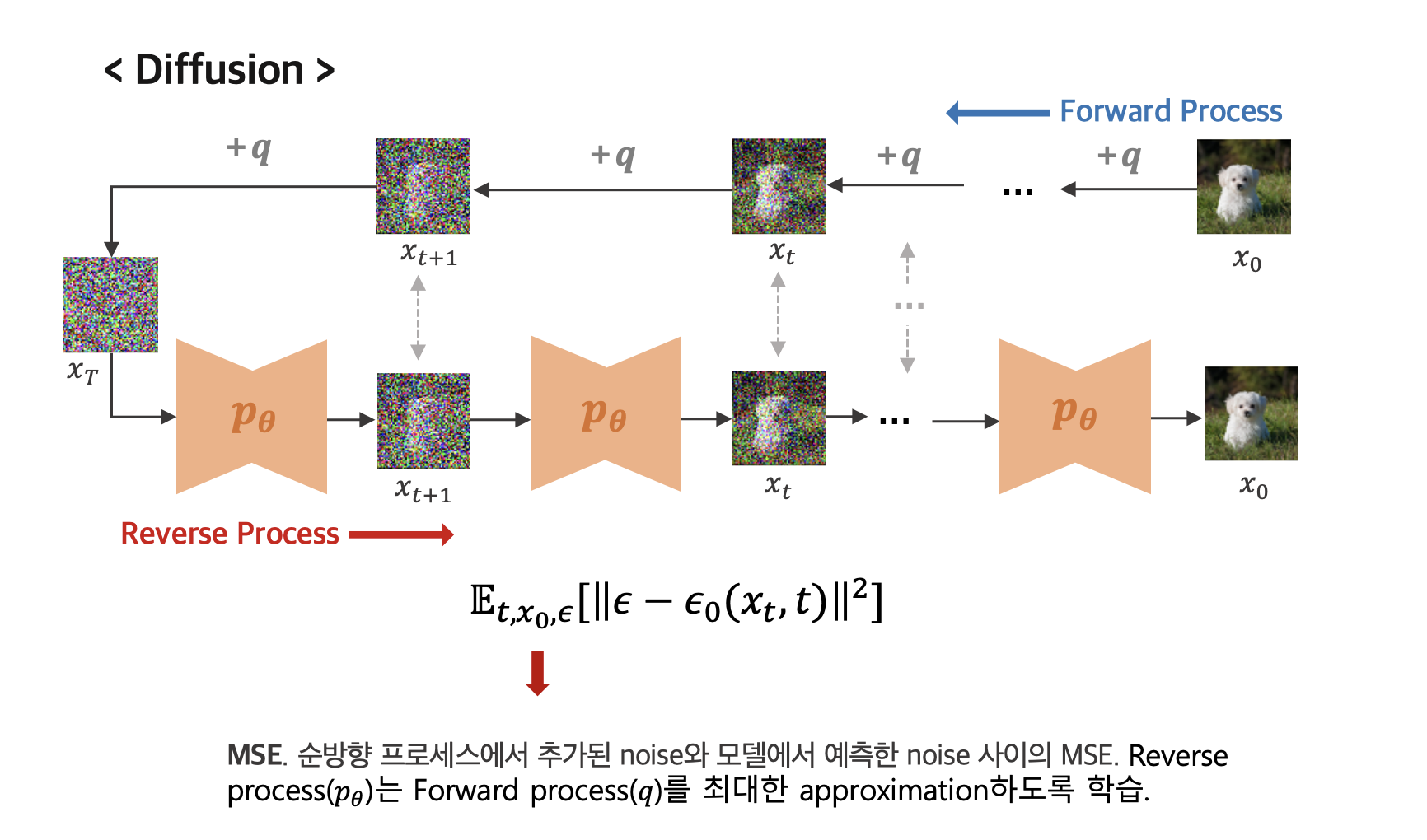
반면에 DDPM은 forward과정과 Backward과정으로 process가 나눠져 있다.

• forward process : Gaussian Noise를 조금씩 추가한다.

• backward process : 이미지에 있는 Gaussian Noise의 분포를 예측하여 Noise를 걷어낸다.

이러한 과정을 $T$번 반복한다. ( 논문에서는 1000번을 반복함.)

한번에 Noise를 추가하지 않고 여러번 나눠서 하는 이유

물론 한번에 Noise를 추가하면 모델이 간단해지겠지만 원본 이미지의 비선형적인 구조를 간단한 가우시안에서 한번에 예측한다는 것이 거의 불가능하다. ( 학습 정보할 정보가 없다는 것)

반면 여러번 반복할 경우 각 단계의 변화율은 적어지게 되고 모델이 학습하기 더욱 쉬워지게 된다.(적은 변화가 많아짐 -> 학습할 정보가 많아짐)
따라서 학습의 안정성이 커진다.

자 이제 우리는 모델의 전체 구조를 알게되었다.

---

Loss function

이제는 학습이 어떻게 할 지 배워야 한다.

Loss function은 VAE와 형태가 거의 똑같다.

유도도 동일하게 $\log p_{\theta}(x_0)$부터 시작한다.

VAE Loss

DDPM Loss

유도 과정은 다음과 같다.

기본적으로 Bayes rule과 Markov Chain이 사용되었다.

이렇게 Loss에 대한 수식이 완성되었다.

하지만 여기서 내가 든 생각은 "그래서 P, q는 어떻게 구하는 건데?" 였다.

정보를 찾다 p와 q의 유도과정에 대해 쓴 글을 찾아냈고 이 글을 자세히 살펴보기로 결정했다.

---

$q(x_t|x_{t-1})$ 계산방법

우리는 VAE에서 사용하는 Reparameterization Trick기법을 알고 있을 것이다.

Reparameterization Trick은 $z$를 $N(\mu, \sigma)$의 분포에서 sampling한다고 했을 때, $z = \mu + \sigma \times \epsilon$ ($\epsilon$ ~ $N(0, I)$) 를 통해 sampling을 하는 기법이다.

샘플링을 하는 부분은 backpropagation이 불가능하기 때문에 Reparameterization Trick을 사용하여 sampling했었다.

우리는 이 기법을 사용하여 $q(x_t|x_{t-1})$의 수식을 유도할 것이다.

하지만 수식을 유도하기 전 나는 한가지 궁금증이 들었다.

이렇게 sampling을 한 $z$가 $N(\mu, \sigma)$의 분포에서 sampling한 것과 동일한가?

따라서 나는 sampling 수식을 사용하여 원본 분포와 동일한 분포가 되는지 확인해보았다.

원본 분포를 $N(x_t;\sqrt{1-\beta_t}x_{t-1}, \sqrt{\beta_t}I)$라고 가정함

원본의 분포와 동일한 분포에서 sampling한 것과 같다는 것을 확인할 수 있었다.

우리는 Reparameterization Trick기법을 재귀적으로 사용하여 $x_{t-1}$에서 Noise를 추가하는 과정을 다음과 같이 표현할 수 있고, 이 수식을 재귀적으로 쓸 수 있다는 점을 이용하여 아래와 같이 표현이 가능하다.

$\epsilon$은 $N(0, I)$를 따른다.

수식을 유도하는 과정에 대해서 별도의 설명없이 $\sqrt{1-\alpha_t\alpha_{t-1}}$이 된 것을 확인할 수 있는데, 나의 필기부분의 빨간 줄을 잘 따라가보자.

$\epsilon$에 대한 수식을 모두 합쳐 z라고 표현한다면, 이 분포에서도 Reparameterization Trick이 가능해진다.

따라서 다음과 같이 표현이 가능한 것이다.

그렇다면 다음과 같이 표현된다는 것도 이제 알 수 있다.

이 과정들이 전부 Reparameterization Trick을 사용한 수식의 변형이라는 것을 알 수 있다.

이렇게 구한 $x_t$의 표현식을 사용하여 $q(x_{t-1}|x_t, x_0)$를 구해보자

우리는 가우시안 노이즈를 더하고 제거하기 때문에 가우시안 분포의 수식을 사용해서 식을 전개한다.

이때 주의해야할 점은 $q(x_{t-1}|x_t, x_0)$는 $x_t \rightarrow x_{t-1}$(1단계이동) 이기 때문에 분산이 $\beta_t$가 된다.

위의 방식과 같은 방식으로 $q(x_{t-1}|x_0)$는 t-1단계 이동이기 때문에
분산이 $1-\bar{\alpha}_{t-1}$이 된다.

세번째 term도 마찬가지

우리는 첫 번째, 두 번째 term을 이용해서 가우시안 분포의 수식형태를 만들 것이다. (우리가 표현할 수 있는 평균과 분산을 구하기 위함)

우리는 성공적으로 $q(x_{t-1}|x_t, x_0)$의 평균과 분산을 구했다!

이제 이 수식의 $x_0$를 $x_t$의 형태로 바꿔줄 것이다.

이제 평균과 분산의 최종형태를 구한 것이다.

잠이온다..

좀만 더 버티자 아자아자~

이제 정답이 아닌 우리가 예측할 확률분포의 수식 $p_{\theta}(x_{t-1}|x_t)$에 대해서 구해보자.

차이는 바로 이전에 구한 평균과 분산의 식에 sampling값을 $\epsilon_{\theta}$으로 바꿔준 것 밖에 없다. ( 파라미터에 의해 sampling되기 때문에 바꿔줌 )

우리는 이제 비로소 DDPM논문의 Loss값을 볼 수 있다.

첫 번째 항과 두 번째 항은 제거가 된다.

첫번째 항은 가우시안 노이즈에서 정답분포의 KLD이므로 학습되는 파라미터가 존재하지 않는다. 따라서 제거한다.

세번째 항은 1번과 0번만 고려한 NLL이므로 영향력이 적어 제거한다.

따라서 두번째 $L_{t-1}$의 항만 loss로 사용한다.

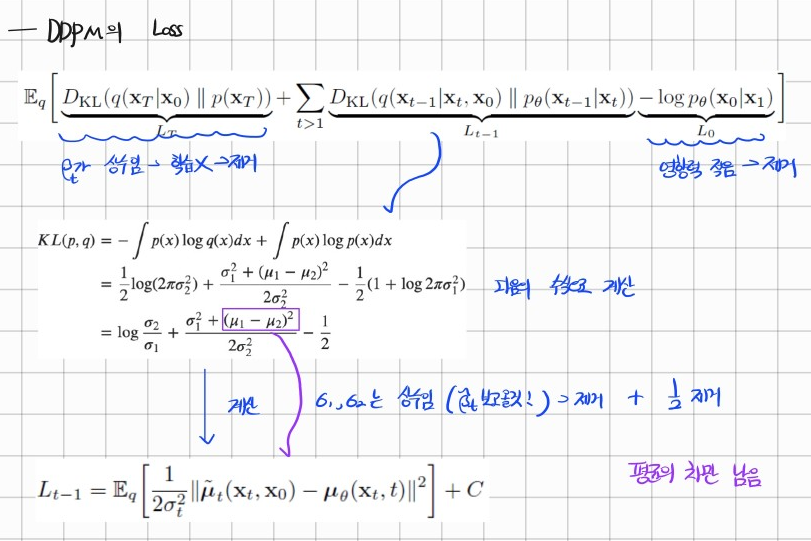
우리는 이제 $q(x_{t-1}|x_t, x_0), p_{\theta}(x_{t-1}|x_t)$의 분산이 모두 상수라는 것을 안다.

$\alpha_t$는 $1-\beta_t$이기 때문 ( $\beta_t$는 Noise를 얼마나 섞어줄지에 대한 비율 -> 스케쥴링이 따로 존재하기 때문에 학습 가능한 파라미터가 아님 -> 분산이 상수가 된다.)

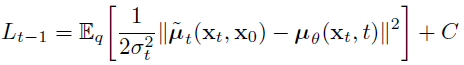
따라서 이 수식이 DDPM의 최종 Loss식이 되는 것이다!

이상으로 포스팅을 마치도록 하겠다~