SkipNet(2017): Learning Dynamic Routing in Convolutional Networks

오늘 리뷰할 논문은 skipnet이다.
layer를 건너뛰어서 연산량을 줄이는 아니디어를 사용했다는 점이 마음에 들었다.

논문의 저자는 resnet의 아이디어를 차용해서 skipnet을 만들었다고 한다.
residual block 앞에 skip-gate를 두어 해당 블럭을 skip 할지말지 정하는 것이다.

그런데 논문을 읽으면서 궁금했던 점이 skip 할지말지에 대한 정보는 continuous한 값이 아니기 때문에 backpropagation을 어떻게 적용할까? 였다.

이 논문에서는 별도의 tensor값을 하나 두고 해당 값에 sigmoid를 사용해 확률값으로 변환을 시켰다고 한다. (이 확률값이 skip을 할 확률이다.)

$X^i$는 i번째 layer의 초기값이다.
$G^i(X^i)$는 layer를 통과할지 정해주는 확률 값이다.
Training에는 GD를 사용하여 학습을 해야하기 때문에 soft-gating방식을 사용했다고 한다. (위의 방식이 soft-gaing방식)

그렇다면 정확도와 연산량을 모두 고려한 loss는 어떻게 만들 수 있을까?

$F_\theta$는 네트워크의 layer들이다. ($F_\theta$는 gating module을 포함함)

여기서 $\theta$는 모델의 parameter를 의미한다.

g는 gate의 값으로 0 또는 1이 나올 수 있습니다.

전체 objective function은 다음과 같습니다.

L은 cross entropy loss고 $R_i$는 i번째 layer의 연산량을 의미합니다.
만약 $g_i$ 는 i번째 layer의 skip gate값을 의미합니다.

$g_i$ = 0 -> skip
$g_i$ = 1 -> excute

스킵한다 -> $g_i$ = 0 -> $R_i$ = 1
스킵하지 않는다 -> $g_i$ = 1 -> $R_i$ = 0

$R_i$ 값(computation 이득에 따른 보상) 이 항상 1일 수 있는 이유는 각 block이 residual block앞에 skip-gate가 붙어있기 때문 ( 연산량이 동일하다. )

스킵을 한다면 $R_i$ = 1이기 때문에 cross entropy loss에서 값을 뺴주는 것을 볼 수 있습니다.
스킵한다면 보상을 주는거죠

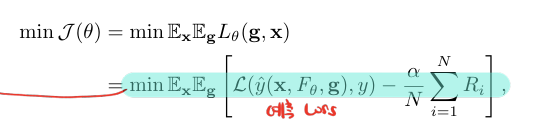
• min cross entropy - skip한 layer에 따른 보상의 평균

결과적으로 $J$($\theta$) 를 최적화시킨다는 것은 정확도와 computation양을 고려한 모델을 만든다는 것을 의미하게 되는 것이죠

우리는 이 식을 최적화해야 합니다.
하지만 loss에 있는 $g_i$는 이산값을 가지죠.

미분이 불가능한 이 식을 사용해서 어떻게 weight update를 할까요?

이 논문에서는 Training과 Test의 예측과정에 차이를 두는 방식을 사용합니다.

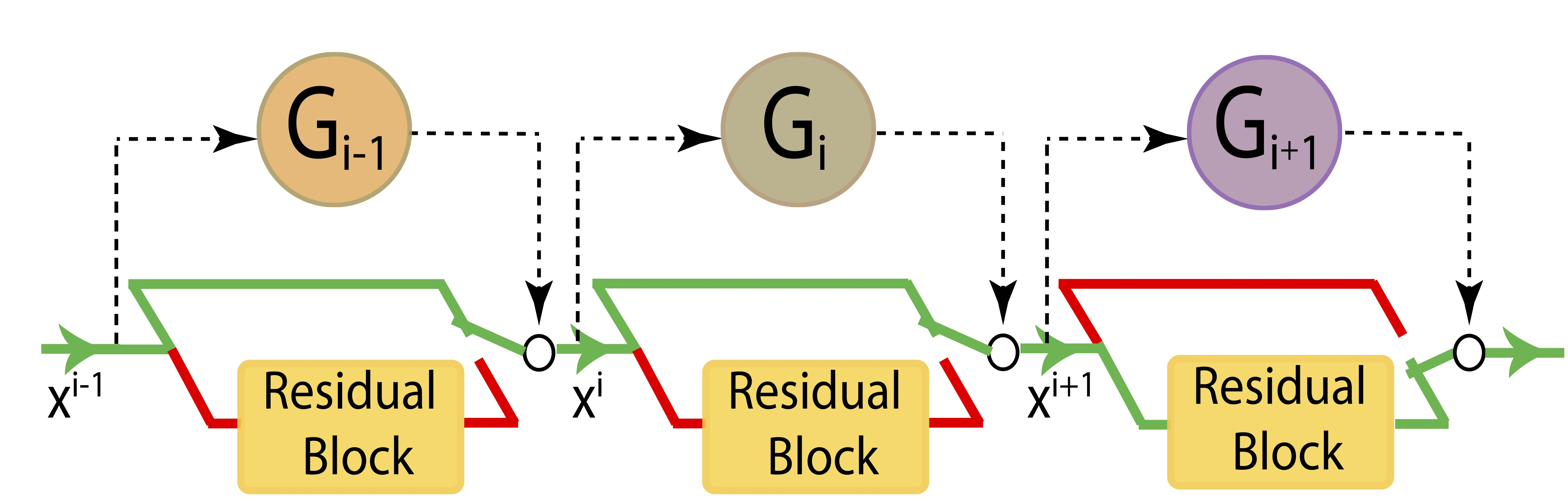
위의 사진이 모델의 구조입니다.

저자는 이 residual block안에 softmax를 넣고 softmax의 두번째 값을 skip할 확률 값으로 씁니다.

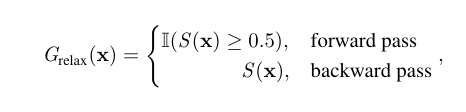
확률값은 미분이 가능하기 때문에 GD로 학습이 가능한거죠

그리고 Test환경에서는 조건문을 추가해서 skip-gate의 확률이 일정 threshold값(논문에서는 0.5)을 넘기면 이 layer를 skip하는 방법을 씁니다.

이상으로 포스팅 마치겠습니다.