Theoretical Limitations of Self-Attention in Neural Sequence Models(2020)

0.0. Abstract

이 논문은 Transformer 기반 모델의 이론적 한계를 탐구하며, 특히 Self-Attention 메커니즘의 표현력을 분석합니다. Transformer는 언어 모델링, 기계 번역, 사전 학습된 컨텍스트 임베딩 생성 등 여러 자연어 처리(NLP) 작업에서 탁월한 성과를 보여왔지만, 이 논문은 이들이 계층적 구조(hierarchical structures)를 처리하는 데 근본적인 제한이 있음을 수학적으로 증명합니다​

1.0. Introduction

Transformer는 순차적인 반복 계산(recurrent computation)을 사용하지 않고 Self-Attention 메커니즘을 기반으로 하여 입력 시퀀스를 병렬적으로 처리합니다. 이 특성 덕분에 긴 시퀀스 처리에 강점을 가지며, 최근 NLP 발전의 중심적인 역할을 해왔습니다. 그러나 이러한 구조는 입력을 순차적으로 처리하지 않기 때문에, 계층적 구조를 정확히 표현하거나 복잡한 순서를 이해하는 데 제한이 있다는 지적이 있었습니다.

논문에서는 두 가지 문제를 중심으로 이 한계를 탐구합니다:

• PARITY 문제: 비트열에서 1의 개수가 짝수인지 홀수인지 결정하는 작업으로, 길이가 유한 상태인 언어의 대표적 문제입니다.
• 2DYCK 문제: 두 가지 괄호 유형이 포함된 균형 잡힌 괄호 문자열을 인식하는 문제로, 계층적 구조를 모델링하는 데 필수적인 문법적 복잡성을 나타냅니다.

💡 연구의 핵심 목표

이 논문은 Self-Attention 메커니즘이 다음과 같은 이론적 한계를 가진다는 점을 증명합니다:

• Self-Attention은 계층적 구조와 순환(recursion)을 포함한 비정규 언어(context-free languages)를 제대로 처리할 수 없습니다.

• 입력 길이에 따라 모델의 레이어 수 또는 매개변수의 크기를 증가시키지 않으면, 이러한 구조적 언어를 완벽히 학습하는 것이 불가능합니다.

2.0. Self-Attention

Self-Attention은 Transformer 모델의 핵심 요소로, 입력 시퀀스의 모든 요소가 서로를 참조(refer)하여 가장 중요한 정보를 추출합니다. 이를 통해 단어 간의 관계를 모델링하고, 문맥을 이해하는 데 사용됩니다.

Transformer는 입력 시퀀스를 병렬로 처리하며, 특정 단어나 토큰이 다른 토큰에 얼마나 집중해야 하는지를 계산하기 위해 Self-Attention 메커니즘을 활용합니다.

Transformer의 입력
Transformer의 입력은 시퀀스 $X = (x_1, x_2, ..., x_n)$으로 표현됩니다. 여기서 각$x_i$는 특정 단어나 토큰을 나타냅니다.

• 각 입력 $x_i$는 임베딩 벡터 $v_i∈R^k$ 로 변환이 됩니다.

• 위치 정보도 모델링하기 위해 positional embedding $p_i∈R^k$ 가 사용됩니다.

• 입력 embedding과 positional embeddig은 결합되어 초기 Layer vector $y_i^{(0)}$로 표현됩니다.

$y_i^{(0)} = f(v_i, p_i)$

여기서 $f$는 임베딩과 위치 정보를 결합하는 함수입니다.

Self-Attention의 계산 과정
Transformer는 𝐿개의 레이어로 구성되며, 각 레이어 𝑘 에서의 상태$y_i^{(k)}$는 Self-Attention 메커니즘과 Feedforward Network(FFN)를 통해 계산됩니다.

$a_{i,j}^{(k,h)} = f_{\text{att}}^{(k,h)}\left(\mathbf{y}_i^{(k-1)}, \mathbf{y}_j^{(k-1)}\right)$

여기서 $f_{att}$는 두 벡터를 입력으로 받아 어텐션 스코어를 계산하는 함수입니다. attention score는 스케일된 내적으로 계산될 수 있습니다.

$a_{i,j}^{(k,h)} = \frac{\mathbf{q}_i^{(k,h)} \cdot \mathbf{k}_j^{(k,h)}}{\sqrt{d_k}}$

• Key vector의 정의: $\mathbf{q}_i^{(k,h)} = W_Q \mathbf{y}_i^{(k-1)}, \quad$
• Query vector의 정의: $\mathbf{k}_j^{(k,h)} = W_K \mathbf{y}_j^{(k-1)}$

Attention의 가중치 계산
이 논문에서는 Soft Attention과 Hard Attention을 나눠서 설명하고 있습니다.
두가지 모두 설명하겠습니다.

Soft Attention에서는 Softmax 함수를 사용하여 각 점수를 확률로 변환합니다.
$\hat{a}_{i,j}^{(k,h)} = \text{softmax}_j(a_{i,j}^{(k,h)}) = \frac{\exp(a_{i,j}^{(k,h)})}{\sum_{j=1}^n \exp(a_{i,j}^{(k,h)})}$

Hard Attention의 경우, 가장 큰 점수를 가지는 위치에만 집중합니다.
$\hat{a}_{i,j}^{(k,h)} = \delta_{j, \arg\max_{j'} a_{i,j'}^{(k,h)}}$

Attention 결과 계산

각 헤드의 결과는 가중치와 이전 레이어 vector $y_j^{(k-1)}$의 가중합으로 계산됩니다.

$\mathbf{b}_i^{(k,h)} = \sum_{j=1}^n \hat{a}_{i,j}^{(k,h)} \mathbf{y}_j^{(k-1)}$

Layer 출력 계산

헤드의 출력을 합쳐 최종 출력을 계산합니다.
$\mathbf{y}_i^{(k)} = \text{FFN}\left(\mathbf{y}_i^{(k-1)}, \mathbf{b}_i^{(k,1)}, \ldots, \mathbf{b}_i^{(k,H)}\right)$

3.0. Results for Hard Attention

이 섹션에서는 Self-Attention 기반 Transformer가 Hard Attention 설정에서 겪는 이론적 한계를 다룹니다. 이 섹션은 특히 PARITY 문제와 2DYCK 문제를 해결하지 못하는 이유를 수학적으로 증명합니다.

Hard Attention이란?
Hard Attention은 Soft Attention과 달리, 모든 입력 위치를 고려하지 않고 특정 위치에만 집중하는 메커니즘입니다. 주어진 위치에서 가장 높은 어텐션 점수를 가지는 입력만 선택됩니다. 이는 다음과 같이 정의됩니다:

$\hat{a}_{i,j} = \delta_{j, \arg\max_{j'} a_{i,j'}}$

여기서:

• $\hat{a}_{i, j}$: 위치 $j$에서의 가중치
• $\arg\max_{j'} a_{i,j'}$: 가장 높은 Attention점수를 가진 입력 위치 $j'$.
• $\delta$: 선택된 입력에만 집중하고 나머지는 무시하는 크로네커 델타 함수.

Hard Attention의 한계 증명

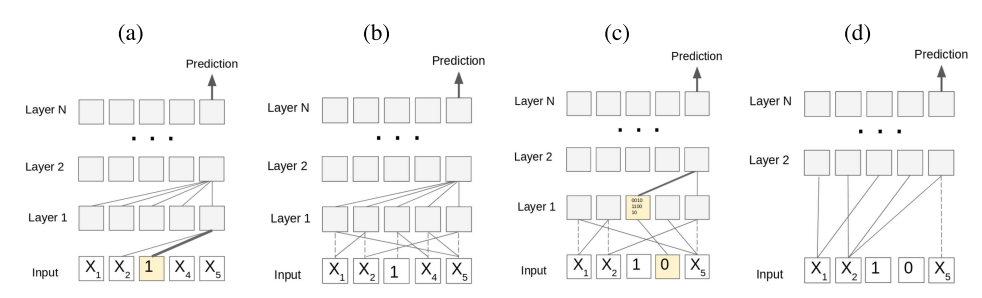
논문에서는 입력 제한(restriction) 𝜌를 도입하여 Transformer의 표현력을 분석합니다. 입력 제한은 일부 입력을 고정(fixed)하고, 나머지 입력만 학습에 활용되도록 합니다.

• $ρ_n(i) ∈ \{0, 1, *\}$:
  - 0 또는 1: 해당 입력은 고정.
  - *: 자유롭게 학습 가능.
  

제안된 정리는 다음과 같습니다.
$|i≤n:ρ_n(i)=*|≥ C_n$

여기서 $C ∈(0,1)$이며, 이는 자유로운 입력의 비율이 $C_n$ 이상임을 보장합니다. 하지만 Hard Attention에서는 출력이 최대 𝑐개의 입력에만 의존하므로, PARITY 문제에서 필요한 모든 입력 비트를 고려하지 못합니다.

결론적으로, 입력 길이 𝑛이 충분히 길어지면, Transformer는 일부 입력의 변화가 결과에 영향을 미치지 않으므로, 정확하게 PARITY 문제를 해결할 수 없게 됩니다.

2DYCK 문제와 Hard Attention의 한계
2DYCK 문제는 두 종류의 괄호(예: ‘(’, ‘)’와 ‘[’, ‘]’)로 구성된 문자열에서 괄호가 올바르게 짝지어져 있는지 확인하는 작업입니다. 예를 들어:

• 올바른 문자열: ([]), [()]
• 올바르지 않은 문자열: (][)

2DYCk는 계층적 구조를 모델링하기 위한 간단한 문제입니다.

Hard Attention의 한계 증명
2DYCK 문제는 문자열의 전역적인 구조를 파악해야 하며, 특히 괄호의 짝이 맞는지 확인하기 위해 모든 입력 간의 상호작용이 필요합니다. 그러나 Hard Attention에서는 다음과 같은 이유로 이를 해결할 수 없습니다:

EX)

1. 입력의 일부를 고정하는 제한ρ를 적용합니다.

   • 처음 0.2n개의 입력은 (로 고정.
   • 마지막 0.2n개의 입력은 )로 고정.
     

2. 나머지 0.6n의 입력은 자유롭게 학습 가능합니다.

3. 그러나 Hard Attention은 출력이 c개의 입력에만 의존하므로, 전체의 입력에 대해서 고려할 수 없습니다.

결론적으로, 2DYCK 문제를 정확히 해결하지 못하며, 더 복잡한 구조를 가진 2DYCK 문제에서도 동일한 한계를 가집니다.

3.1 Proving the Depth Reduction Lemma

논문의 Depth Reduction Lemma는 Self-Attention 모델의 레이어 깊이를 축소할 수 있는 수학적 과정을 설명합니다. 이 섹션에서는 입력 제한(𝜌)을 정의하고, 이를 세 가지 단계로 나누어 설명합니다. 여기서는 첫 번째와 두 번째 단계인 Stage 1과 Stage 2, Stage 3의 증명 과정을 정리합니다.

Stage 1: Layer 0의 입력 제한
목표:
입력 제한을 통해 Layer 0의 각 입력 비트가 의존하는 Attention Head의 수를 제한합니다.

과정:
1. 주어진 입력제한 $ρ_n$을 시작점으로 사용합니다.
2. Layer 0의 각 입력 비트 $i$가 $\frac{1}{\eta} \frac{c}{C}$ 개 이상의 Attention Heads에 의존하지 않도록 제한합니다.
3. 만약 $\eta Cn$ 이상의 입력 비트가 $\frac{1}{\eta} \frac{c}{C}$개 이상의 Layer 0 Activation에 의존한다고 가정한다면, 가능한 활성화 조합의 수를 초과하게 됩니다. 이는 다음과 같이 증명됩니다.

$\text{Number of Pairs} > \eta Cn \cdot \frac{1}{\eta} \frac{c}{C} = nc$

하지만 Layer 0의 활성화 개수는 최대 n개이고, 각 활성화는 c개의 입력에만 의존하므로 가능한 조합의 수는 nc 이하입니다. 이로부터 $\eta Cn$이상의 입력 비트가 $\frac{1}{\eta} \frac{c}{C}$개 이상의 활성화 함수 부분에 의존할 수 없음을 알 수 있습니다.

따라서 이러한 조건을 만족하지 않는 입력비트를 고정 값 0 or 1로 제한하여 새로운 제한 $ρ_n^{(1)}$을 생성합니다.

결론
새로운 제한 $ρ_n^{(1)}$는 다음을 만족합니다.
$| \{ i \leq n : \rho^{(1)}_n(i) = * \} | \geq (1 - \eta)Cn$

이는 충분히 큰 𝑛에 대해 여전히 많은 입력 비트가 자유롭게 남아 있음을 의미합니다.

• $\frac{1}{\eta} \frac{c}{C}$는 어떻게 나왔는가?
  $\frac{1}{\eta} \frac{c}{C}$는 한 입력 비트가 연결될 수 있는 Layer-0 activation의 최대 개수를 의미합니다.

1. $C_n$: 전체 입력 길이 n에서 제한되지 않은 입력 비트의 총 개수 입니다.
   즉, $C$는 입력 비트 중 자유롭게 사용할 수 있는 비율을 나타냅니다.
2. $\eta Cn$: 문제가 되는 입력 비트의 수
   여기서 $\eta ∈ (0, 0.5)$는 상대적으로 작은 값으로, 문제가 되는 입력 비트의 비율을 제한하기 위한 상수입니다.
3. 각 Layer-0 activation이 최대 $c$개의 입력 비트에 의존할 수 있으므로, $n$개의 Layer-0 activation은 총 $nc$개의 입력 비트를 수용할 수 있습니다.
4. 한 입력 비트가 영향을 미칠 수 있는 Layer-0 activation의 최대 수는:
   $\frac{Layer-0 activation의 총 개수}{문제가 되는 입력 비트의 개수}$ = $\frac{nc}{\eta Cn}$ = $\frac{c}{\eta C}$

따라서, 문제가 되는 입력 비트가 영향을 미치는 Layer-0 activation의 최대 개수는 $\frac{1}{\eta}$ $\cdot$ $\frac{c}{C}$로 유도됩니다.

---

Stage 2: Layer 1 Attention Head의 입력 제한

목표:
Layer 1의 각 Attention Head가 Layer 0의 활성화 중에서 최대$k$개의 입력에만 의존하도록 제한합니다.
과정

1. Layer 0에서의 활성화 $y_i^{(0)}$는 최대 $c$개의 입력에 의존하므로, 가능한 값의 수는 다음과 같이 제한됩니다.
   $|y^{(0)}_i| \leq 2^c$

2. Layer 1의 Attention Head $(h, i)$가 특정 Layer-0 활성화 $y_i^{(0)}$에 집중하는 최대 Attention값을 계산합니다.
   $\max_{x_1, \ldots, x_n : y^{(0)}_i = z} f_{\text{att}, 1, h}(z, y^{(0)}_j)$
   여기서 $z$는 $y_i^{(0)}$의 가능한 값입니다.

3. 각 Attention Head$(h, i)$에 대해 $k$개의 입력 위치를 선택합니다. 이 위치는 다음 조건을 만족해야 합니다.

   • 각 입력 $x_q$는 선택된 활성화 하나에만 기여합니다. (max값으로 선택된 것만 사용함.)
   • $x_q$는 다른 선택된 위치 $i_{s'}^{(z)}$ (s'과 s는 다름)에는 영향을 미치지 않습니다.
   • $i_k^{(k)}$는 작아져야 한다.

💡 $i_k^{(k)}$가 작아져야 하는 이유?

$i_k^{(k)}$가 최소화된다는 조건은, 선택된 k개의 위치 중 가장 큰 인덱스의 수가 최대한 작게 유지되도록 선택한다는 뜻 입니다.
처음에는 좀 헷갈리는 표현이었는데 생각해보면 다음과 같다.
attention weight의 크기 순으로 정렬을 하고 그 정렬된 값에 index를 매긴다.
이후 매긴 인덱스에서 k개를 나눠서 선택한다. 가장 attention weight가 낮은 k번째 weight의 index가 작다면 모델이 고려하는 weight의 개수가 작아지기 때문에 입력공간이 더 작아진다.
-> 입력공간을 효율적으로 줄이기 위해 필요함

새로운 제한 $ρ_n^{(2)}$은 다음을 만족합니다.

$| \{ i \leq n : \rho^{(2)}_n(i) = * \} | \geq (1 - 2\eta)Cn$

stage1에서 $\eta$만큼 입력 비트가 고정이 되었고, stage2에서 $\eta$만큼 입력비트가 고정되었기 때문에 남아있는 비트의 비율은 다음과 같이 표현할 수 있다.

논문에서 $\rho_n^{(2)}$의 생성에 대해서는 다음과 같이 나와있습니다.

• 특정 Layer-0 activation이 > $2^ckH$개의 unsatisfied Layer-1 head에 영향을 미칠 수 있다.

• $y_j^{(0)}$는 c개의 입력비트에 의존한다.

• $y_j^{(0)}$의 값을 고정하면 Layer-0 activation은 > $kH$개의 Layer-1 head를 만족시킬 수 있다.

Layer-1 head의 전체 개수는 입력길이 $n$에 대해서 각 위치 $i$에서 H개의 attentnion head가 존재하기 때문에 총 Layer-1 head의 개수는 $nH$라고 볼 수 있다.

💡만족(satisfied)의 정의가 무엇일까?
1. $(h, i)$가 Layer-0 activation $y_j^{(0)}$들 중 상위 $k$개의 activation에만 의존함.
2. 이 상위 $k$개의 activation 중 적어도 하나가 $\rho_n^{(2)}$에 고정된 값을 가져야 함.
3. 고정된 값은 Attention score를 최대화하는 $z$에 대해서 설정되어야 함.

즉, $(h, i)$가 "만족된다"라는 것은:

• $y_j^{(0)}$가 고정된 값을 가짐으로써 $z$에 대해 최대 Attention score를 계산할 수 있다.
• 결과적으로 $(h, i)$는 다른 Layer-0 activation이나 입력 비트의 값 변화에 영향을 받지 않음을 의미한다.

반복 횟수 제한 $(U)$

1. 반복당 해결 가능한 head의 수:

• 한번의 고정으로 $K \cdot H$개의 Layer-1 head가 해결이 된다. (Layer-0 activation이 정해진다는뜻), 전체 $n \cdot H$개의 head를 모두 만족시키기 위해 필요한 최대 반복 횟수는:
  $U ≤ \frac{n \cdot H}{k \cdot H}$ = $\frac{n}{k}$ 가 된다!

2. 고정할 수 있는 Layer-0 activation 수 고려:

• 각 Layer-0 activation $y_j^{(0)}$는 $2^c$개의 가능한 $z$값을 가질 수 있으므로, 최악의 경우 $2^c$개의 반복이 필요하다.
• 따라서 반복횟수의 제한은 다음과 같이 표현이 가능하다.
  -> $U ≤ \frac{2^c \cdot n}{k}$

stage1에서 우리는 문제가 되는 bit들을 고정했었다. 그렇기 때문에 $\rho^{(1)}_n$에서 제한되지 않은 입력 비트는 다음과 같아진다.
$| \{ i \leq n : \rho^{(2)}_n(i) = * \} | \geq (1 - \eta)Cn - c$

나는 왜 c값을 빼는지 처음에는 잘 이해가 가지 않았다.
알고보니 Layer-0 activation의 문제가 되는 출력 값을 고정해야 되기 때문에 Layer-0 activation이 의존하는 bit의 최대 개수인 c를 뺸 것이었다.
Layer-0 의 출력값에서 문제가 되는 부분의 bit가 최대가 되었을 때 자유비트의
개수가 $(1 - \eta)Cn - c$이므로 실제 자유비트의 개수는 이 값보다 크거나 같게 된다. ( 이 수식은 한 번의 반복 과정에서 비트를 최대로 제한했을때의 경계값을 말한다.)

이 수식은 $\rho^{(2)}_n$ 가 생성될 때, 제한되지 않은 비트가 충분히 많이 남아 있음을 보장하기 위한 최소 조건을 나타냅니다.

반복 조건이 만족될 때 상태
반복 조간이 종료된 후, 제한되지 않은 비트의 수는 다음의 수식을 만족한다.

$| \{ i \leq n : \rho^{(2)}_n(i) = * \} | \geq (1 - \eta)Cn - cU$

여기서:

• $(1-\eta)Cn$: 초기 $\rho^{(1)}_n$에서 제한되지 않은 bit 수.

• $cU$: 반복 과정에서 고정된 비트의 총 개수.

$K$의 선택 조건
$k$를 충분히 크게 선택하여 다음 조건을 만족시키자.

$\frac{2^c \cdot n}{k}$ ≤ $\eta$

이렇게 된다면 $U ≤ \frac{2^c \cdot n}{k}$ 이기 때문에 반복이 종료된 이후에도 제한되지 않은 입력 비트의 개수가 충분히 많음을 보장한다.

$| \{ i \leq n : \rho^{(2)}_n(i) = * \} | \geq (1 - 2\eta)Cn$

이렇게 된다면 모든 Layer-1 head가 $k$-dependency를 만족하도록 보장하게 된다.

💡 k-neighbors란 무엇인가?
k-neighbors는 Layer-1 attention head간의 간접적인 의존성을 나타냅니다.
두 Layer-1 head $(h, i)$와 $(h', j)$가 동일한 입력 비트 $x_i$에 의존할 경우, 이 두 head는 k-neighbor관계에 있다고 정의됩니다.

K-neighbor의 상한 계산
K-neighbors는 입력 비트 간 의존성을 통해 형성되기 떄문에, 한 Layer-1 head의 k-neighbors의 수는 k-dependency와 $c^2$-Transformer 구조적 제약을 고려해 다음과 같이 계산됩니다.

$f$ ≤ $\frac{2^{2c}\eta c^2k^2H}{C}$

이 수식은 unsatisfied Layer-1 head에서 k-neighbors의 최대 개수를 나타냅니다.

이 수식은 추후에 더 살펴봐야 될 것 같다.

---

Stage 3: 확률적 방법을 사용

Stage 3에서는 다음을 보장하기 위해 $\rho^{(3)}_n$를 생성합니다. 이는 Stage3에서 생성된 $\rho^{(3)}_n$를 기반으로 입력 비트를 추가로 고정하며, 모든 Layer-1 head가 만족상태가 되도록 보장합니다.

1. 목표

• stage3에서는 다음을 보장하기 위해 $\rho^{(3)}_n$를 생성:
  1. 모든 $X0$ 및 $X_i^{(z)}$ 사건을 회피(avoid)
  2. 제한되지 않은 입력비트(즉, $\rho^{(3)}_n$ = * )의 개수가 충분히 많이 유지.
  3. 최종적으로 만든 Layer-1 head가 상위 $k$개의 Layer-0 activation에만 의존하도록 보장
  

2. 사건의 정의
   (1) 사건 $X_0$

   • $X_0$: $\rho^{(3)}_n$가 $\rho^{(2)}_n$에서 *로 남아있던 입력 비트 중 > (1 + $\delta$)q 만큼을 0 또는 1로 고정했을 때 발생하는 사건
   • 여기서:
     - q: 각 입력 비트가 0, 1, 로 설정될 확률 중 로 남은 확률은 1-q.
     - $\delta$: 허용 오차로 , q의 비율을 초과하는 경우를 방지

   (2) 사건 $X_i^{(z)}$

   • $X_i^{(z)}$: 특정 Layer-1 head (h, i)에서 상위 k개의 Layer-0 activation이 고정된 값을 가지지 못했을 때 발생하는 사건.
     - Layer-1 head가 만족되지 않음을 나타냄.
     - $z$: 가능한 $y_i^{(0)}$의 조합 중 하나.

3.확률적 방법으로 사건 회피

(1) 확률적 고정 과정

• 각 입력 비트를 0, 1, *로 랜덤하게 설정

  • 1: 확률 q/2
  • 0: 확률 q/2
  • *: 확률 1-q
    

(2) 사건 $X_0$가 발생할 확률
$X_0$ 는 고정된 입력 비트 수가 허용된 비율을 초과했을 때 발생합니다. $X_0$발생 확률은 Chernoff Bound를 사용하여 계산됩니다:

$P(X_0) \leq \exp\left(-\frac{\delta^2 q (1 - 2\eta)Cn}{3}\right)$

(3) 사건 $X_i^{(z)}$가 발생할 확률

$X_i^{(z)}$는 특정 Layer-1 Attention Head가 상위 k 개의 Layer-0 활성화 값에 의존하지 못했을 때 발생합니다. 발생 확률은 다음과 같이 계산됩니다:

$X_i^{(z)} = \bigcap_{t=1}^k Y_t^{(z)}$

• $Y_t^{(z)} : \text{Layer-0 활성화 } y_j^{(0)} \text{가 특정 Attention Head에서 최대 가중치를 생성하지 못하는 사건.}$
• $Y_t^{(z)}$의 발생 확률
• $P(X_i^{(z)}) \leq \left(1 - \left(\frac{q}{2}\right)^c \right)^{\frac{\eta c^2}{Ck}}$

(4) k-neighbors 수 $f$
각 사건은 제한된 수의 k-neighbors와 상호작용합니다. k-neighbors의 개수는 다음과 같이 계산됩니다.

$f \leq \frac{2^{2c} \eta c^2 k^2 H}{C}$

(5) Lovász Local Lemma 조건
Lovász Local Lemma를 적용하여 모든 사건을 회피할 수 있도록 설정합니다. Lemma의 조건은 다음과 같습니다:

$P(X_i(z)) \leq A(1 - B)(1 - A)^f$

$P(X_0) \leq B(1 - A)^{2^c Hn}$

여기서:

• A = $\frac{1}{k^2}$
• B = $\frac{1}{2}$

Lovász Local Lemma 조건에 대해서는 추후 공부할 예정입니다.

(6) 최종 입력 의존성

1. Stage3 이후 남아있는 자유 입력 비트의 개수는 다음과 같습니다.

   $\left| \{ i \leq n : \rho^{(3)}_n(i) = * \} \right| \geq (1 - 2\eta)(1 - (1 + \delta)q)Cn$

2. Layer-1 Attention Head 만족
   모든 Layer-1 Attention Head가 상위 𝑘개의 Layer-0 활성화 값에만 의존하도록 보장합니다.

3. Layer-1 Attention Head의 입력 의존성은 다음과 같이 제한됩니다:

   $c \cdot \left(2^c k H + 1\right)$

---

4.0. Results for Soft Attention

SOFT ATTENTION의 주요 분석 목표
논문에서는 Soft Attention이 가진 한계를 다음과 같은 두 가지 측면에서 분석합니다:
1. 개별 입력 비트의 영향 감소: 특정 입력 비트가 출력에 미치는 영향은 $O(\frac{1}{n})$으로 감소하며, 이는 입력 길이 $n$이 증가할수록 더욱 작아집니다.
2. 교차 엔트로피 손실 증가: Soft Attention 구조에서는 정확한 출력을 예측하지 못하는 경우 Cross entropy loss가 높아집니다.

4.1. 입력비트가 출력에 미치는 영향

정의

• Transformer의 Layer $k$에서 , 두 입력 $x$와 $x'$가 단 하나의 입력 위치 $i$만 다른 경우의 차이를 분석합니다.
• 각 레이어에서의 활성화 벡터 차이$||y_j^{(k)} - {y'}_j^{(k)}||$로 정의하며, 이를 레이어 깊이에 대해서 유도합니다.

기본 가정

• 입력 벡터 $x$와 $x'$의 차이는 $i$번째 위치의 임베딩 차이 $\|v^{(k)}_i - v'^{(k)}_i\|$로 나타내며, 이를 D라고 정의

$D$ = $\|v^{(k)}_i - v'^{(k)}_i\|$

결과

• $i$번쨰 위치에서 활성화 차이는 Layer k에 대해서 다음과 같이 감소했다.

$\|y^{(k)}_i - y'^{(k)}_i\| \leq C 2^k D$

• $j$, $i$가 다를 경우, 다른 위치의 활성화 차이는 $n$의 크기에 반비례하여 감소

$\|y^{(k)}_j - y'^{(k)}_j\| \leq \frac{H^{k-1} C 2^{k-1} D}{n}$

설명

• 특정 입력 비트의 영향은 레이어가 깊어질수록 $2^k$로 증폭되지만, 다른 위치의 활성화 값에서는 $O(\frac{1}{n})$으로 감소
• 따라서 입력 비트 하나가 전체 출력에 미치는 영향은 매우 작아지며, 이는 Soft Attention 구조에서 각 입력의 정보가 희석됨을 의미.

4.2 교차 엔트로피 손실 증가

정의

• 주어진 입력 ( x )에서 다음 기호를 예측하는 작업:
  1. 열림/닫힘 괄호 또는 시퀀스 종료(ENDOFSEQUENCE)를 예측.
  2. 닫힘 괄호인 경우, 둥근 괄호 ( ')' ) 또는 대괄호 ( ']' )를 예측.

결과

Soft Attention이 닫힘 괄호를 무작위로 선택해야 하는 경우, 최소 교차 엔트로피 손실은 다음과 같음:

$\text{Loss} \geq P_0 \cdot (1 - p) \cdot \log 2$

여기서:

• $( P_0 )$: 입력 $( x )$가 특정 조건(예: 닫힘 괄호로 끝남)을 만족할 확률.
• $( p )$: 특정 괄호가 뒤따를 확률.
• $( \log 2 )$: 두 선택지(둥근 괄호와 대괄호)가 동등하게 선택될 경우의 불확실성.

4.3. 유도 과정: 입력 차이에 따른 활성화 변화

레이어 ( k = 0 )에서의 활성화 차이

• 입력 ( x )와 ( x' )의 차이는 ( i )-번째 입력 벡터 차이 ( D )로 정의:

$\|y^{(0)}_i - y'^{(0)}_i\| \leq D$

$\|y^{(0)}_j - y'^{(0)}_j\| = 0 \quad (j \neq i)$

레이어 ( k > 0 )에서의 활성화 차이

Attention Score의 상한

• $( y^{(k)}_j )$의 Attention logit은 상수 $( A )$로 상한을 가짐:

• $a_{j,i}^{(k)} \leq \frac{\exp(A)}{\exp(A) + (n - 1)\exp(-A)} \leq \frac{\exp(2A)}{n - 1}$

활성화 차이의 유도

1. $( y^{(k)}_i )$와 $( y'^{(k)}_i )$의 차이는 다음과 같이 증가:

$\|y^{(k)}_i - y'^{(k)}_i\| \leq C 2^k D$

2. $( j \neq i )$의 경우:

$\|y^{(k)}_j - y'^{(k)}_j\| \leq \frac{H^{k-1} C 2^{k-1} D}{n}$

4.4 입력 비트의 영향 감소

입력 비트 하나가 출력에 미치는 영향:

$\|y^{(k)}_j - y'^{(k)}_j\| = O\left(\frac{1}{n}\right)$

이는 Soft Attention이 멀리 떨어진 입력 간의 관계를 효과적으로 학습하지 못함을 의미.

4.4 교차 엔트로피 손실 증가

Soft Attention 구조에서는 최적의 교차 엔트로피 손실보다 다음 값만큼 추가 손실 발생:

$P_0 \cdot (1 - p) \cdot \log 2$

4.5 Soft Attention의 한계

• 레이어 깊이 ( k )와 입력 길이 ( n )에 따라, 입력 간 상호작용의 영향이 감소.
• 이는 Transformer가 고정된 깊이 ( L )에서 멀리 떨어진 입력 간 관계를 충분히 학습하지 못하는 이유를 수학적으로 설명.

---

5.0. 결론

1. 이론적 한계

(1) 비-카운터프리 정규 언어

• Transformer는 비-카운터프리(Non-Counterfree) 정규 언어를 모델링할 수 없습니다.

  카운터프리 언어란? 입력 문자열의 특정 패턴(예: 괄호 짝 맞춤, 균형 조건)을 구별하는 데 카운팅(Counting)이 필요하지 않은 언어.
  비-카운터프리 언어는 카운팅이 필요하므로, Transformer의 구조적 한계로 인해 이를 처리하지 못합니다.
  예: PARITY(짝수/홀수 판단), 2DYCK(이진 괄호 짝 맞춤).

(2) 기본적인 계층적 구조 (Hierarchical Structure)

• Transformer는 기본적인 계층적 구조도 처리하지 못합니다.
• • 계층적 구조는 문법적 언어에서 흔히 볼 수 있는 특성으로, 괄호 구조나 중첩된 종속성이 이에 해당합니다.
• • 예: 자연어에서 종속 절(subordinate clause) 또는 문장 중첩 구조.

(3) Hard Attention vs. Soft Attention

• Hard Attention:
  Activation 함수나 파라미터 크기와 상관없이, Transformer는 Hard Attention에서 비-카운터프리 언어를 정확히 분류할 수 없습니다.
• Soft Attention:
  Soft Attention에서는 결과가 약간 덜 일반화되지만, 여전히 Transformer가 완벽한 교차 엔트로피(cross-entropy)를 달성할 수 없음을 보입니다.
  입력 길이가 증가할수록 이러한 한계는 두드러집니다.

(1) 무한한 입력 길이에 대한 한계

• 논문의 결과는 입력 길이 𝑛이 충분히 길어질수록 Transformer가 PARITY나 2DYCK 언어를 처리하는 데 오류를 범할 수밖에 없음을 보여줍니다.
• • 즉, Transformer는 무한히 긴 입력에서는 근본적으로 한계를 가집니다.
• • 이는 Transformer 구조가 멀리 떨어진 입력 간 상호작용을 충분히 학습하지 못하기 때문입니다.

(2) 짧은 입력에서의 성능

• 하지만, 입력 길이가 짧은 경우 Transformer는 높은 정확도나 교차 엔트로피를 달성할 수 있습니다.
• • 입력 길이에 상한 𝑁을 설정하면, 𝑛≤𝑁에 대해 완벽한 정확도를 달성하는 Transformer를 설계할 수 있습니다.
• • 이 경우, Layer 수, Head 수, 또는 파라미터 크기는 입력 길이 𝑁에 따라 증가해야 합니다.

결론적으로, 이 논문은 Transformer의 한계를 보여주지만, 현실적인 제약을 완전히 설명하지는 못하며, 자연어 처리와 같은 실제 응용에서 Transformer는 아직도 좋은 도구로 쓰인다고 말하고 있습니다.

이 논문을 읽으면서 무지의 슬픔을 많이 느꼈습니다. 😢