이번 스터디 그룹 모임의 주제는 "Geometry".

도형이나 공간의 성질을 분석하여 관련 문제 해결 능력을 기르기 위한 주제였다.

기하학적 문제들을 해결하다 보니 단순히 기하학적인 문제 해결 능력뿐 아니라 다차원 배열의 데이터나 패턴이 있는 데이터를 다루는 능력을 기르는 데에도 도움이 될 것 같아서 꾸준히 공부해야 할 영역이라고 느껴졌다.

사실 이번 스터디 모임을 통해서 기하학적 문제 해결 능력보다는 다양하게 생각해 봐야겠다는, 특히 파이썬스럽게 생각하는 습관을 길러야겠다는 깨달음이 더 컸다.

이번 글에서는 Python 언어를 통해 [Baekjoon Online Judge] 사이트에 있는 기하학 문제들을 풀고 스터디 그룹원들과 함께 리뷰해 보는 과정을 통해 느낀 점을 기록해 본다.

핵심은 PATTERN 찾기

도형이나 공간의 성질에 따라 패턴이 나타나고 그 패턴을 활용하여 문제를 해결해야 했다.

그러 패턴을 찾아나가는 과정에 있어서 주어진 데이터를 활용하는 방법이 사람마다 달라서 굉장히 흥미로웠다.

그리고 그런 부분이 가장 두드러진 문제가 [2477번: 참외밭] 문제였다.

[2477번: 참외밭] 문제 [문제 링크]

참외 밭은 위와 같이 ㄱ-자 모양이거나 ㄱ-자를 90도, 180도, 270도 회전한 모양(┏, ┗, ┛ 모양)의 육각형이다. 이 밭의 넓이를 구해야 하는데 임의의 한 꼭짓점에서 출발하여 반시계 방향으로 둘레를 돌면서 지나는 변의 방향과 길이 데이터를 입력받아 활용해야 한다.

PATTERN 1

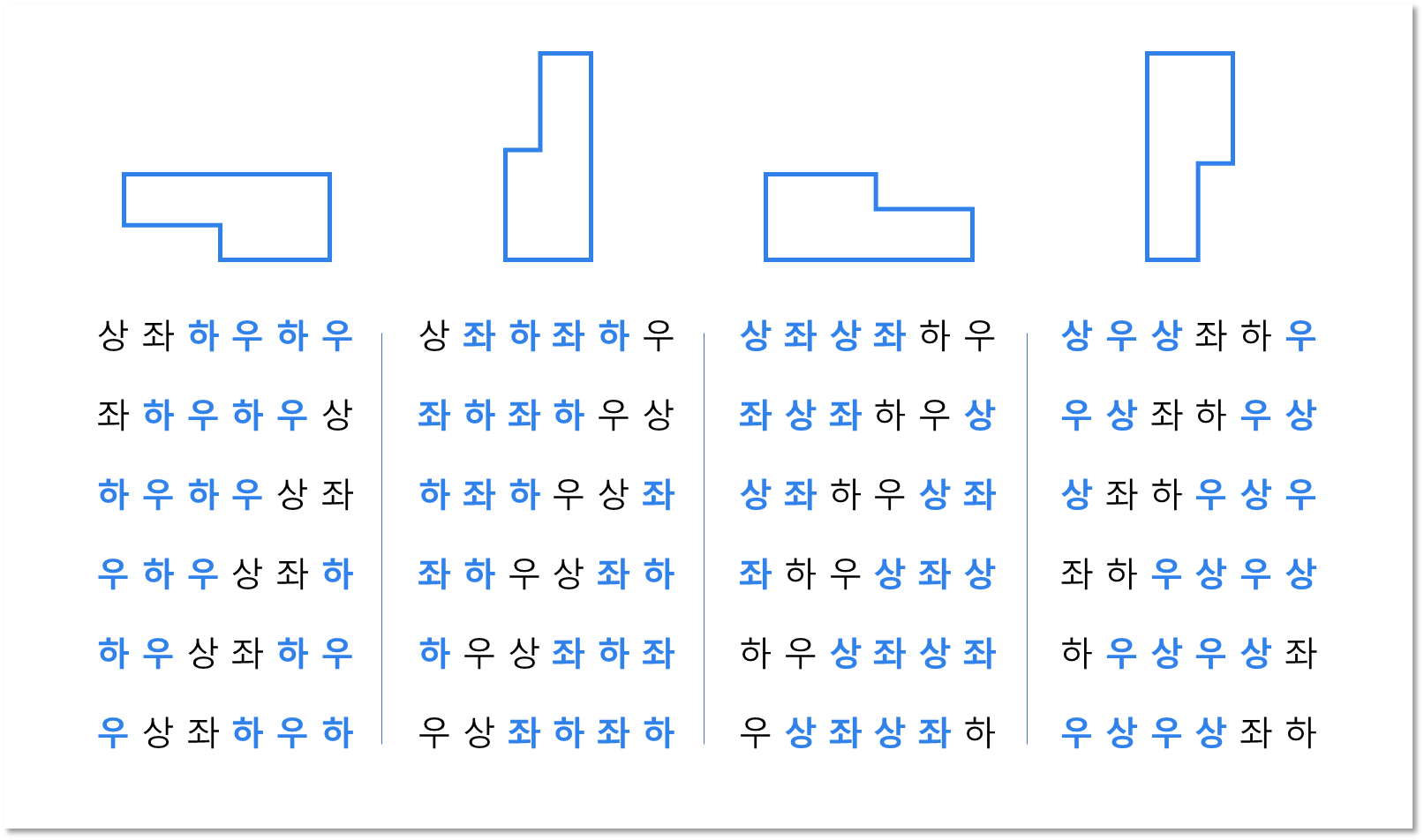
위 그림은 $ㄱ$자 모양의 밭이 회전한 모양에 따라 나올 수 있는 모든 경우의 방향 입력 값이다.

각 모양마다 입력받은 상, 하, 좌, 우 방향 값들을 두 번 나열하면 왼쪽 모양부터 차례로 아래와 같이 반드시 등장하는 배열이 있다.

• 하 우 하 우
• 좌 하 좌 하
• 상 좌 상 좌
• 우 상 우 상

이 패턴을 활용하신 분의 알고리즘은 이랬다.

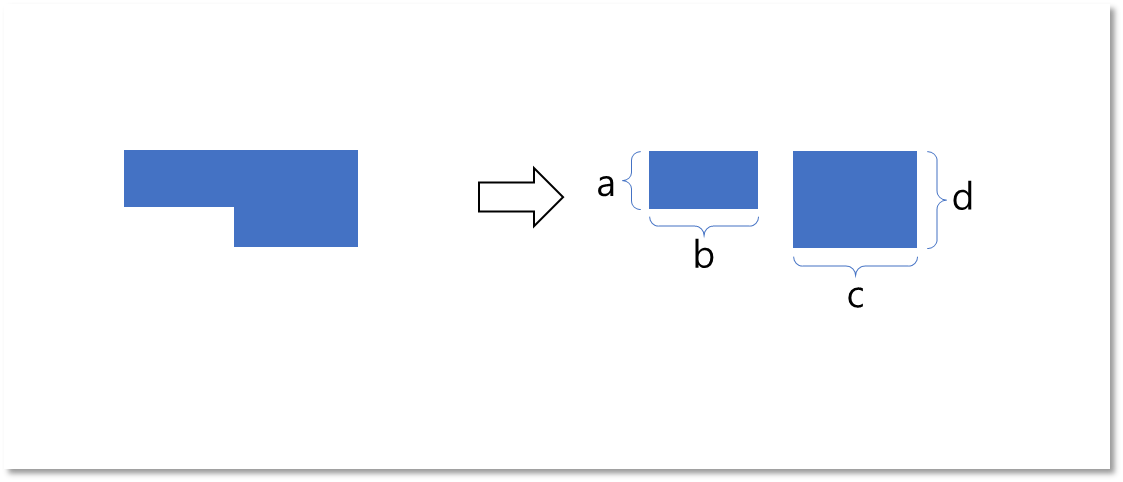
• 큰 직사각형의 넓이 구하기
  • 세로 길이 (상, 하) 중 가장 큰 값과 가로 길이 (좌, 우) 중 가장 큰 값을 곱한다.
• 작은 직사각형의 넓이 구하기
  • 방향 입력값을 두 번 나열한다.
  • 하우하우, 좌하좌하, 상좌상좌, 우상우상 중 일치하는 패턴을 찾는다.
  • 찾은 패턴의 2, 3번째 값에 대응하는 길이 값을 서로 곱한다.
• 큰 직사각형의 넓이에서 작은 직사각형의 넓이를 뺀 값이 답이다.

$w \times h - x \times y = Answer$

PATTERN 2

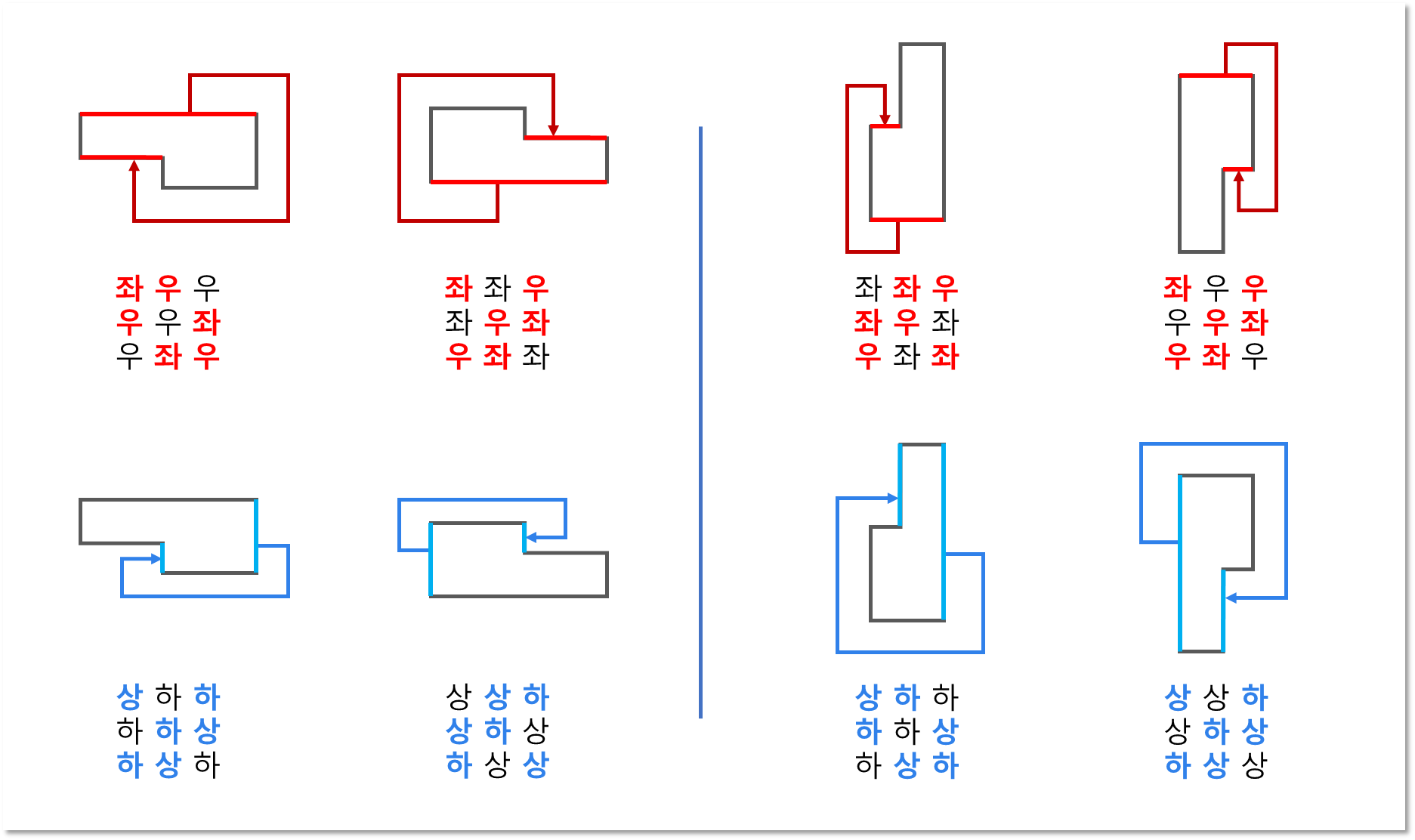
위 그림은 $ㄱ$자 모양의 밭이 회전한 모양에 따라 나올 수 있는 모든 경우의 방향 입력 값을 좌우와 상하 방향을 따로 나누었을 때의 모습이다.

그리고 ㄱ, ㄴ 모양일 때와 ┘, ┌ 모양일 때 각각 그림처럼 계산에 필요한 변을 찾을 수 있는 패턴이 있다.

이 패턴을 활용하신 분의 알고리즘은 이랬다.

• 각 방향과 이에 대응하는 길이의 값을 좌우, 상하로 나누어 변수에 저장한다.
• ㄱ, ㄴ모양일 경우:
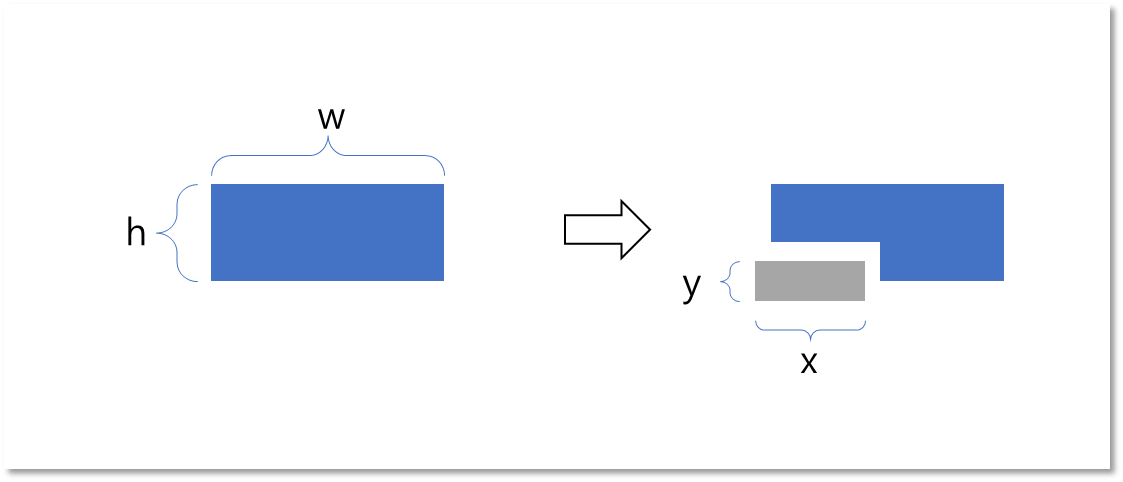
  • 좌, 우 길이 중 긴 값을 $w$라 하고 $w$의 인덱스 값 $-2$에 해당하는 인덱스의 값을 $x$라 한다.
    (예시 1: 좌우 길이 = [w, x, 나머지 값])
    (예시 2: 좌우 길이 = [x, 나머지 값, w])
    ($w$의 인덱스 $+1$의 경우 out of index 에러가 날 수 있어서 $-2$로 계산.)
  • 상, 하 길이 중 긴 값을 $h$라 하고 $h$의 인덱스 값 $-1$에 해당하는 인덱스의 값을 $y$라 한다.
• ┘, ┌ 모양일 경우:
  • 좌, 우 길이 중 긴 값을 $w$라 하고 $w$의 인덱스 값 $-1$에 해당하는 인덱스의 값을 $x$라 한다.
  • 상, 하 길이 중 긴 값을 $h$라 하고 $h$의 인덱스 값 $-2$에 해당하는 인덱스의 값을 $y$라 한다.
• $w \times h - x \times y = Answer$

PATTERN 3

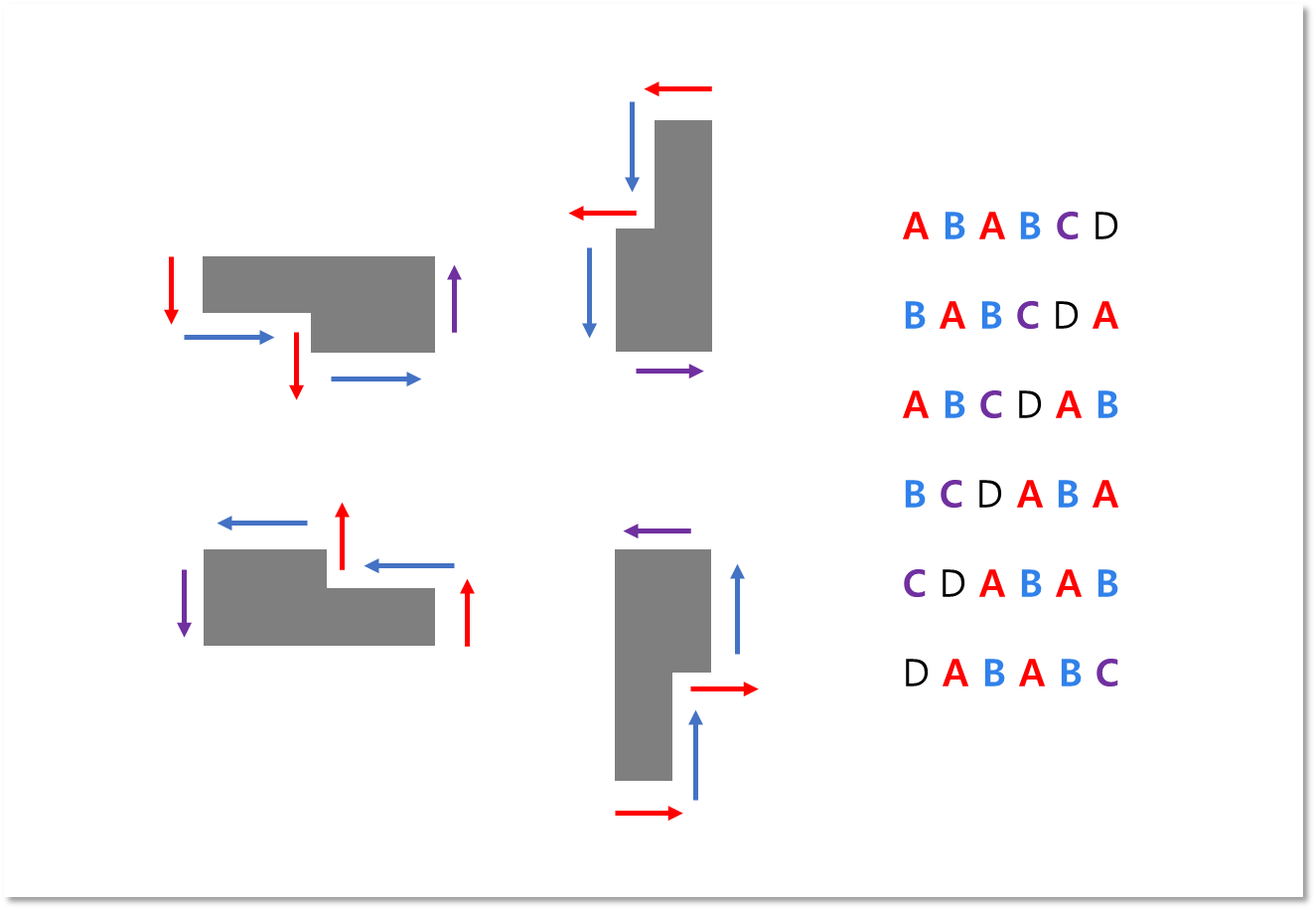
위 그림은 밭이 어떤 방향으로 회전한 모양이든 나올 수 있는 모든 방향 입력값의 패턴이다.
즉, A가 상, 하, 좌, 우 중 어느 것이든 두 번 반복된다는 점, 그리고 어느 꼭짓점을 시작으로 입력받느냐에 따라 위의 그림과 같은 6 가지 중 하나일 수밖에 없다는 점에 따른 패턴인 것이다.

그리고 첫 번째 입력값을 가장 뒤로 보내는 것을 반복하면 5번 안에 반드시 아래와 같은 패턴을 갖게 된다.

• A B A B C D
  즉, 어떤 꼭짓점부터 방향 값을 입력받기 시작해도 위의 패턴으로 만들어 계산할 수 있다.

이 패턴을 활용해서 내가 만든 알고리즘은 이랬다.

• 입력받은 패턴이 A B A B C D 인지 확인한다.
  • 아니라면 첫 번째 입력값을 가장 뒤로 보내고 다시 확인한다.
  • A B A B C D 패턴이 될 때까지 반복한다. (재귀)
• A B A B C D 패턴이 되면 첫 A와 첫 B 값에 대응하는 길이를 서로 곱한다. ($= a \times b$)
• A B A B C D 패턴에서 두 번째 B 값과 C 값에 대응하는 길이를 서로 곱한다. ($= c \times d$)
• 앞서 구한 값을 서로 더한 값이 답이다. ($a \times b + c \times d = Answer$)

$a \times b + c \times d = Answer$

느낀 점

언제나 다른 방법이 있다

매번 느끼는 것이지만, 하나의 결과를 만들기 위한 방법은 참 다양하다.

새삼 이번 스터디 모임에서도 또 그 생각이 들었다.

같은 데이터를 가지고 같은 결과를 만들어내기 위해 서로 다른 패턴을 찾아냈다는 점도 신기했고 연산 방식이 다른 것도 상당히 재미있었다.

특히, list에서 out of index 에러를 피하기 위해 인덱스에 덧셈 연산 대신 뺄셈을 사용한 것도 굉장히 놀라웠다. 인덱스에 덧셈 연산을 활용해서 코드를 작성하다가 out of index 때문에 엎은 적이 있었는데 새로운 방법을 알게 돼서 좋았다. 나중에 꼭 써먹어야겠다.

한국어와 Python 언어는 다르다

외국계 기업에서 일하다 보니 영어로 대화할 일이 많았었다. 그리고 한국어로는 표현이 되는데 영어로 그 표현 직역하자니 도무지 뭐라 해야 할지 모르겠는 경우가 종종 있었다. 그래서 같은 의미이지만 다른 표현으로 바꾸어 설명해야 하는 경우들이 있었다.

결국 Python도 하나의 언어다.

처음 참외 문제를 접했을 때 떠올렸던 방법을 Python 언어로 어떻게 표현해야 할지 몰라서 한참 동안 고민했었다. 그러다가 안되겠다 싶어서 내 수준에서 Python 언어로 표현해낼 수 있는 다른 방법을 찾자고 마음을 바꾸니 금방 다른 방법이 보였고 그렇게 코드를 완성했다.

당장 방법을 알겠는데 Python 언어로 구현하기 어렵다면 Python 언어로 구현해낼 수 있는 방식으로 사고하는 것도 방법이다.

Pythonic Thinking

"It's how the language that you speak shapes the way that you think." - Lera Boroditsky

인지 과학자 보로디츠키는 연구를 통해 "어떤 언어를 사용하는지가 사고방식을 결정한다" 는 것을 밝혀냈다. 그리고 이것은 반대로 그러한 사고방식을 하면 언어를 좀 더 그 언어답게 사용할 수 있다는 의미라고도 할 수 있을 것이다.

즉, 파이썬스럽게 사고하는 습관을 기르면 보다 Pythonic 한, 효율적이고 명료한 코드를 작성할 수 있게 될 것이다.

Pythonic Thinking을 하도록 노력하자.