이번 스터디 그룹 모임의 주제는 지난 주에 이어서"Geometry".
이번 주에 풀어본 문제들은 특정 위치 좌표값이 특정 도형 안팎으로 위치하는지 여부를 묻는 문제들이었다.
덕분에 이후에 평면상의 위치 데이터를 다루거나 3차원 물리 공간 데이터를 다루는데 조금 도움이 될 것 같다는 느낌이 들었다.
이번 글에서는 Python 언어를 통해 [Baekjoon Online Judge] 사이트에 있는 기하학 문제들을 풀고 스터디 그룹원들과 함께 리뷰해 보는 과정에서 느낀 점이 있었던 문제 풀이에 대해 기록해 본다.
문제 풀이
1002번 문제: 터렛
문제 요약
문제를 최대한 간단하게 요약하자면, 두 원의 중심점 위치좌표와 반지름 데이터가 주어지면 두 원의 테두리가 만나는 횟수를 구하는 문제였다.
풀이 요약
첫 번째 원의 중심점 위치:
첫 번째 원의 반지름:
두 번째 원의 중심점 위치:
두 번째 원의 반지름:
우선 두 원의 중심점 사이의 거리를 피타고라스의 정리를 이용해 구한다.
distance
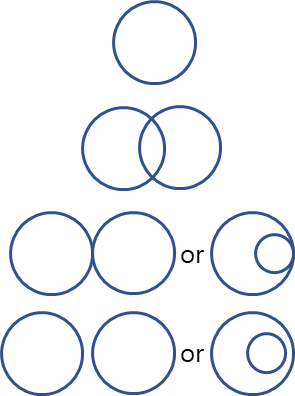
두 원의 테두리가 만나는 경우의 수는 크게 4가지로 볼 수 있다.
-
두 원의 중심점 위치와 반지름이 동일하여 무한히 겹치는 경우
if distance == 0 and r1 == r2 -
두 점에서 만나는 경우
elif abs(r1 - r2) < distance < (r1 + r2) -
한 점에서 만나는 경우 (외접 혹은 내접)
elif r1 + r2 == distance or abs(r1 - r2) == distance -
만나지 않는 경우 (위 조건에 만족하는 않는 나머지 경우)
else
위 4가지 경우의 수를 그림으로 나타내면 아래와 같다.
느낀점
가독성이 좋은 코드와 간결한 코드 중 어느 쪽이 더 나은지 생각해보게 됐다.
스터디 조원 중 한 분은 두 원의 반지름이 같은지 다른지 크게 2가지 경우로 나눈 후 각각에서 다시 한 번 세부 조건으로 나누어 계산했다. 그렇게 세부조건까지 나누니 십여 가지 조건문이 나왔고 세부적으로 나눈만큼 각각의 조건문의 가독성이 높아졌다. 단, 중복되는 조건이 2가지 발생했다.
나와 다른 한 분은 두 원의 중심점이 같은지 다른지 크게 2가지로 나눈 후 각각에서 다시 한 번 세부 조건을 나누었다. 이 경우는 총 약 6가지 정도의 조건문으로 나뉘게 되어 보다 간결해졌으나 가독성이 비교적 떨어졌다.
협업하는 입장에서는 가독성이 좋은 코드가 좋을 것 같다. 이번 문제와 같은 경우 한 번의 연산에서 데이터의 양이 많지 않아 처리 조건문의 양이 차이에도 불구하고 처리 속도에는 영향이 거의 없었다.
이 문제와는 달리 실무에서 많은 양의 데이터를 다룰 때에는 간결하게 연산 횟수를 줄여 처리 속도를 높이는 편이 좋을 것 같다.
그렇다면 내 코드는 충분히 간결했나 싶은 마음에 돌아보니 표현만 다를 뿐 나도 중복되는 조건이 있다는 것을 알게 됐다. 그래서 좀 더 큰 틀에서 나누어 6가지에서 위의 풀이처럼 4가지로 줄일 수 있다는 것을 알게 됐다.
큰 틀에서 생각해야 좀 더 간결하고 처리 속도가 빠른 코드가 나올 것이며 가독성이 떨어지는 부분은 협업하는 사람들을 위해 주석처리를 달아놓는 습관을 들이도록 해야겠다.
1004번 문제: 어린 왕자
문제 요약
여러 원들 사이에 위치한 출발점과 도착점 사이를 오가는 경우에 마주치는 원의 경계의 최솟값을 구해야 한다.
풀이 요약
출발점만을 감싸는 원의 개수와 도착점만을 감싸는 원의 개수를 합하면 된다.
- 둘이 동시에 속한 원의 경계를 지나치지 않아도 되기 때문이다.
- 둘 모두 속하지 않은 원의 경계는 지나치지 않아도 되기 때문이다.
- 어느 한 쪽만 감싸는 원의 경계는 반드시 지나야만 다른 한 점으로 이동할 수 있기 때문이다.
느낀 점
공식에 얽매여서 불필요한 연산을 하지 않도록 주의해야겠다.
스터디 조원들 모두 같은 논리로 풀이를 했다. 하지만 공식대로 하느라 하지 않아도 되는 계산을 했다는 것을 다른 분의 코드를 보여 알게 됐다.
또한, 이 분의 경우 비교 연산자를 통해 좀 더 간결하고 가독성 높은 코드를 완성했다.
같은 방식이지만 보다 깔끔한 표현을 하도록 해야겠다.
정리
- 처리 속도를 위해 불필요한 연산을 피하도록 하자. (효율!)
- 가독성을 위해 주석을 달자.
- 간결하면서도 효율적일 수 있는 방법을 생각해보자.