Convolutional Matrix Factorization for Document Context-Aware Recommendation (ACM 2016)

INTRODUCTION

• 추천의 질을 낮추는 sparsity
• 몇몇 연구에서는 demography 정보를 사용하여 이를 해결하고자 함
• item description을 추출하기 위해 LDA, SDAE 등의 document modeling 방법론이 최근 연구됨
• 하지만 위 두 방법론은 bag-of-words 기반 방법론으로써, 문맥을 고려하지 못함
• 최근 제시된 Novel한 방법론인 CNN은 local 정보를 잘 반영하며 document를 deep하게 파악할 수 있음
  • Glove와 같은 pre-trained 모델을 통해 word embedding을 추출할수도 있음
• 다만 CNN은 추천 task에는 적용하기 힘듬
• 우리의 ConvMF(CNN + PMF)는 이를 적절히 조화시킴
• 이전 document modeling 방법론에서 해소하지 못한 document의 context를 파악하고 SOTA를 달성

PRELIMINARY

Matrix Factorization

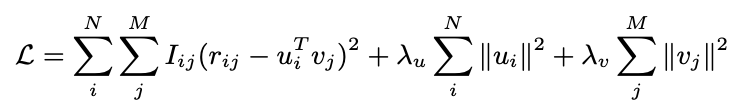
• user vector와 item vector의 dot product로 rating을 예측하는 것
• 다음 목적식을 최소화 함으로써 학습

Convolutional Neural Network

• Variant feed-forward neural networks
  • By convolution, generate local features
    • 로컬 피쳐 생성
  • pooling layer for representation
    • data를 축약 표현
• CNN은 CV에서 origin을 갖지만, NLP Task에서도 좋은 성능을 보임
• 아쉽게도 CNN은 아직 추천시스템 task에 잘 적용되지 않았음
  • van den Oord et al.은 music recommendation에 CNN을 적용했지만, 이는 music signal에만 해당
  • 또한 Weighted matrix factorization의 성능을 넘지 못함

CONVOLUTIONAL MATRIX FACTORIZATION

Probabilistic Model of ConvMF

• $\mathrm{R} \in \R^{m \times n}$, $\mathrm{U} \in \R^{k \times N}$, $\mathrm{V} \in \R^{k \times M}$
• $\mathrm{U^TV} \approx \mathrm{R}$

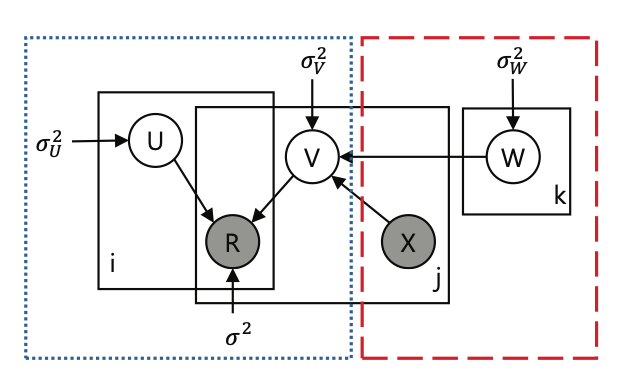
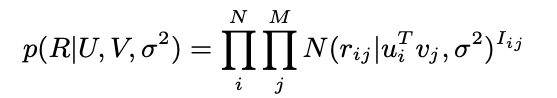
• PMF 관점에서는 다음과 같은 수식이 나옴

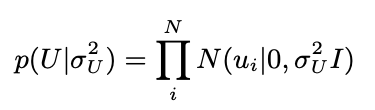
• 유저 벡터는 동일하게 가우시안으로 분포 가정

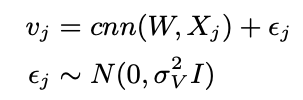
• 아이템 벡터에서 차이가 있는데, item j의 document에 해당하는 Xj를 cnn layer에 통과시킨 후 optimizing을 위한 가우시안 에러를 추가함
• W, Xj, epsilon이 모두 gaussian prior를 갖는다고 가정

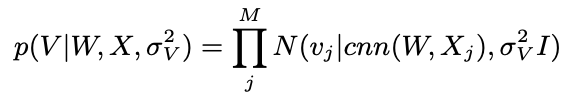
• 따라서 다음과 같은 conditional distribution이 생성됨
• CNN을 통과한 latent vector는 평균으로 활용되고, noise가 분산으로 활용 됨

CNN Architecture of ConvMF

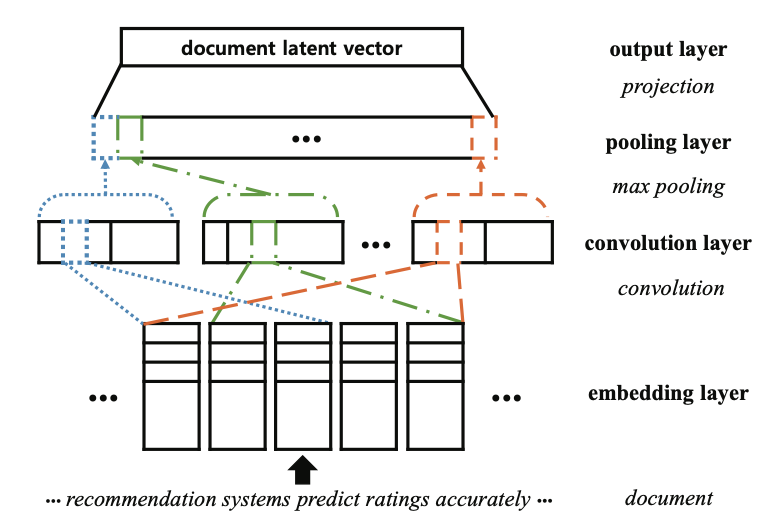
Embedding Layer

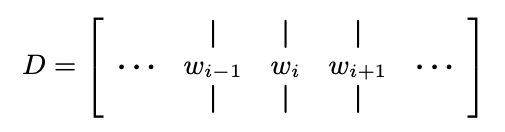
• raw document to dense matrix
• document가 $\mathrm{l}$개의 word이면 embedding은 $\R^{p \times l}$ 차원을 가짐
• $\mathrm{l, p}$ 는 각각 document length와 embedding dimension을 의미

Convolution Layer

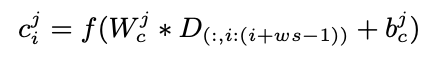
• Document는 inherently different with image
• 따라서 document에서 잘 작동할 수 있게 convolution을 설정해야 함
• $\mathrm{c_i^j} \in \R$, $W_c^j \in \R^{p \times ws}$
• $*$ 는 convolution operator이며, $\mathrm{b_c^j} \in R$ bias, f는 activation function

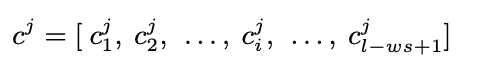
Pooling Layer

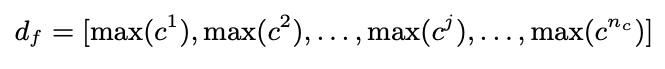
• convolution layer로 뽑아낸 feature를 pooling을 통해 고정된 feature vector로 만들어줌
• 너무 많은 contextual feature는 성능 향상에 도움이 되지 않음
• 고정되지 않은 길이의 contextual feature vector는 학습을 어렵게 함
• 따라서 max-pooling을 활용하여 고정된 길이의 vector로 문서를 표현함
  • 각 feature vector의 max값만 뽑아서 최종 벡터를 구성

Output Layer

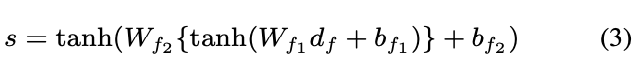
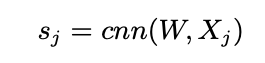
• Fully Connected layer와 activation fuction을 통과하여 최종적으로 아이템 j에 해당하는 document latent vector를 생성 (k차원으로 projection)

Optimization Methodology

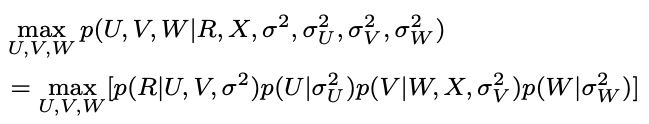
• MAP를 극대화하도록 학습

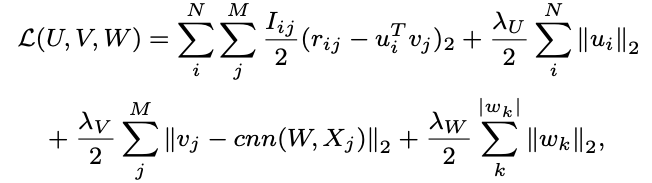
• 다음과 같이 reformulate할 수 있음
• 다른 변수를 고정해놓고, 차례 차례 변수를 학습하는 coordinate descent를 채택

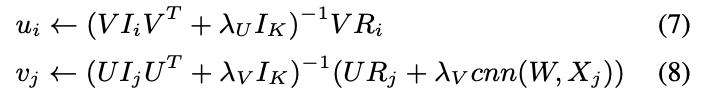
• 다음과 같이 closed form으로 정리 가능

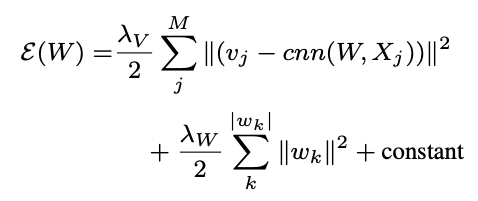
• W는 CNN, max-pooling, non-linear activation 때문에 closed form으로 정리 불가
• 따라서 back propagation algorithm을 통해 optimize (UV term을 일시적으로 constant로 설정)
• U, V, W를 순차적으로 학습하여 수렴할 때 까지 진행

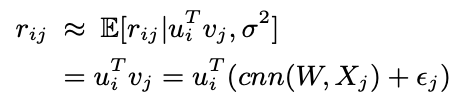
• 예측치는 다음과 같음