AI with GPT - 3. 지도학습

Sylen·2024년 5월 30일

AI with GPT

목록 보기

6/7

챕터 3: 지도학습

지도학습은 기계학습의 한 유형으로, 입력 데이터와 해당 레이블(정답)을 사용하여 모델을 학습하는 방법입니다. 지도학습의 주요 응용 분야는 회귀 분석과 분류입니다. 이번 챕터에서는 회귀 분석에 대해 상세히 다루겠습니다.

3.1 회귀 분석 (Regression Analysis)

회귀 분석은 연속적인 값을 예측하는 기법입니다. 입력 변수와 출력 변수 간의 관계를 모델링하여 예측을 수행합니다.

3.1.1 선형 회귀 (Linear Regression)

개념

선형 회귀는 가장 기본적인 회귀 기법으로, 입력 변수와 출력 변수 간의 선형 관계를 모델링합니다. 선형 회귀 모델은 다음과 같은 형태를 가집니다.

y = \beta_0 + \beta_1 x + \epsilon

여기서 $y$ 는 출력 변수, $x$ 는 입력 변수, $\beta_0$ 는 절편(intercept), $\beta_1$ 는 기울기(slope), $\epsilon$ 은 오차(오차항)입니다.

수식 유도 과정

선형 회귀 모델의 목표는 주어진 데이터에 가장 잘 맞는 직선을 찾는 것입니다. 이를 위해 잔차 제곱합(Residual Sum of Squares, RSS)을 최소화해야 합니다.

잔차 제곱합은 다음과 같이 정의됩니다.

RSS = \sum_{i=1}^{n} (y_i - \hat{y}_i)^2

여기서 $y_i$ 는 실제 값, $\hat{y}_i$ 는 예측 값입니다.

선형 회귀의 계수 $\beta_0$ 와 $\beta_1$ 는 다음과 같은 공식을 통해 구할 수 있습니다.

\beta_1 = \frac{\sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^{n} (x_i - \bar{x})^2}

\beta_0 = \bar{y} - \beta_1 \bar{x}

여기서 $\bar{x}$ 와 $\bar{y}$ 는 각각 $x$ 와 $y$ 의 평균값입니다.

실용적인 코드 예제

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

# 데이터 생성
np.random.seed(0)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)

# 선형 회귀 모델 학습
lin_reg = LinearRegression()
lin_reg.fit(X, y)

# 모델 예측
X_new = np.array([[0], [2]])
y_predict = lin_reg.predict(X_new)

# 결과 시각화
plt.scatter(X, y)
plt.plot(X_new, y_predict, color='red', linewidth=2)
plt.xlabel("X")
plt.ylabel("y")
plt.title("선형 회귀 예제")
plt.show()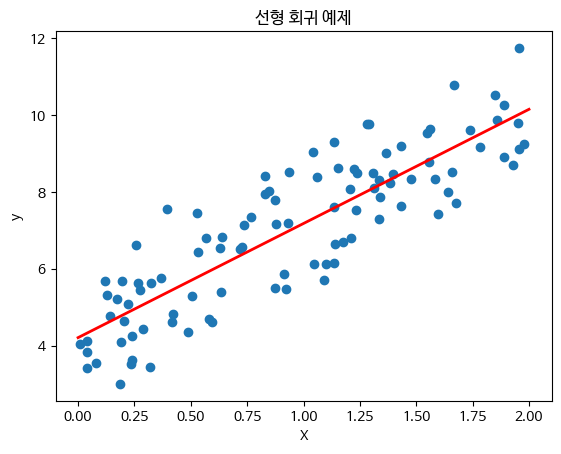

3.1.2 다항 회귀 (Polynomial Regression)

개념

다항 회귀는 선형 회귀의 확장으로, 다항식을 사용하여 입력 변수와 출력 변수 간의 비선형 관계를 모델링합니다. 다항 회귀 모델은 다음과 같은 형태를 가집니다.

y = \beta_0 + \beta_1 x + \beta_2 x^2 + \ldots + \beta_n x^n + \epsilon

여기서 $n$ 은 다항식의 차수(degree)를 나타냅니다.

수식 유도 과정

다항 회귀의 목표는 주어진 데이터에 가장 잘 맞는 다항식을 찾는 것입니다. 이를 위해 선형 회귀와 마찬가지로 잔차 제곱합을 최소화해야 합니다.

다항 회귀 모델의 계수는 선형 회귀와 동일한 방식으로 계산할 수 있지만, 입력 변수 $x$ 를 다항식의 형태로 변환하여 선형 회귀 모델에 적용합니다.

실용적인 코드 예제

import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression

# 데이터 생성
np.random.seed(0)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + 5 * X**2 + np.random.randn(100, 1)

# 다항 회귀 모델 학습
poly_features = PolynomialFeatures(degree=2)
X_poly = poly_features.fit_transform(X)
poly_reg = LinearRegression()
poly_reg.fit(X_poly, y)

# 모델 예측
X_new = np.linspace(0, 2, 100).reshape(100, 1)
X_new_poly = poly_features.transform(X_new)
y_predict = poly_reg.predict(X_new_poly)

# 결과 시각화
plt.scatter(X, y)
plt.plot(X_new, y_predict, color='red', linewidth=2)
plt.xlabel("X")
plt.ylabel("y")
plt.title("다항 회귀 예제")
plt.show()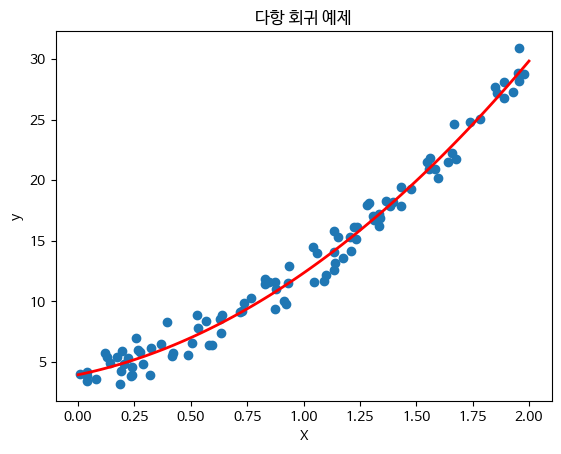

이상으로 지도학습의 회귀 분석 중 선형 회귀와 다항 회귀에 대해 상세히 설명하였습니다. 다음으로 분류 기법들에 대해 다루겠습니다.

Prompt

지도학습의 회귀분석에 대해 더 추가로 설명해줘야 할 내용과 분석방법이 많을것같은데 추가로 상세한 설명과 수식, 유도과정, 기초개념을 포함해서 설명해줄수있을까?

Answer

물론입니다. 지도학습의 회귀 분석에 대해 더 추가로 상세히 설명하겠습니다. 선형 회귀와 다항 회귀 외에도 다양한 회귀 분석 기법과 그에 대한 기초 개념, 수식 유도 과정, 그리고 실용적인 예시를 다루겠습니다.

3.1.3 릿지 회귀 (Ridge Regression)

개념

릿지 회귀는 선형 회귀의 한 종류로, 과적합(overfitting)을 방지하기 위해 L2 정규화(L2 Regularization)를 적용한 모델입니다. 릿지 회귀는 다음과 같은 비용 함수(Cost Function)를 최소화합니다.

J(\theta) = \sum_{i=1}^{m} (y_i - \hat{y}_i)^2 + \lambda \sum_{j=1}^{n} \theta_j^2

여기서 $\lambda$ 는 정규화 강도(Regularization Strength)를 나타내며, $\theta_j$ 는 모델의 파라미터입니다.

수식 유도 과정

릿지 회귀의 목표는 잔차 제곱합과 파라미터 제곱합의 가중 합을 최소화하는 것입니다. 이는 다음과 같이 수식으로 나타낼 수 있습니다.

\hat{\theta} = \arg\min_{\theta} \left( \sum_{i=1}^{m} (y_i - X_i \theta)^2 + \lambda \sum_{j=1}^{n} \theta_j^2 \right)

릿지 회귀는 다음과 같은 형태의 해석적 해(solution)를 가집니다.

\hat{\theta} = (X^T X + \lambda I)^{-1} X^T y

여기서 $X$ 는 입력 데이터 행렬, $y$ 는 출력 벡터, $I$ 는 단위 행렬입니다.

실용적인 코드 예제

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Ridge

# 데이터 생성
np.random.seed(42)
X = 3 * np.random.rand(100, 1)
y = 1 + 0.5 * X + np.random.randn(100, 1)

# 릿지 회귀 모델 학습
ridge_reg = Ridge(alpha=1, solver="cholesky")
ridge_reg.fit(X, y)

# 모델 예측
X_new = np.linspace(0, 3, 100).reshape(100, 1)
y_predict = ridge_reg.predict(X_new)

# 결과 시각화
plt.scatter(X, y)
plt.plot(X_new, y_predict, color='red', linewidth=2)
plt.xlabel("X")
plt.ylabel("y")
plt.title("릿지 회귀 예제")
plt.show()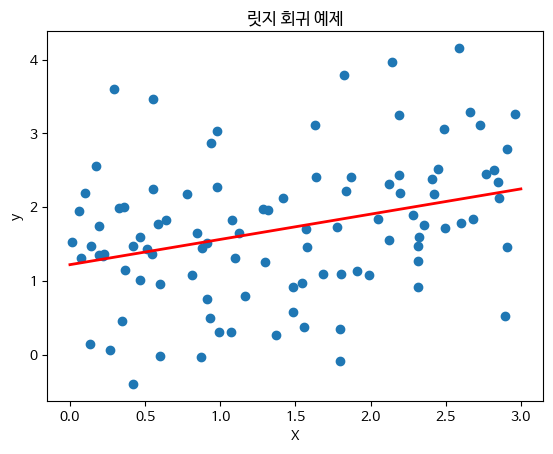

3.1.4 라쏘 회귀 (Lasso Regression)

개념

라쏘 회귀는 선형 회귀의 한 종류로, 과적합을 방지하기 위해 L1 정규화(L1 Regularization)를 적용한 모델입니다. 라쏘 회귀는 다음과 같은 비용 함수를 최소화합니다.

J(\theta) = \sum_{i=1}^{m} (y_i - \hat{y}_i)^2 + \lambda \sum_{j=1}^{n} |\theta_j|

여기서 $\lambda$ 는 정규화 강도입니다.

수식 유도 과정

라쏘 회귀의 목표는 잔차 제곱합과 파라미터 절대값 합의 가중 합을 최소화하는 것입니다.

\hat{\theta} = \arg\min_{\theta} \left( \sum_{i=1}^{m} (y_i - X_i \theta)^2 + \lambda \sum_{j=1}^{n} |\theta_j| \right)

라쏘 회귀는 특성 선택(feature selection)에 유용합니다. 많은 $\theta_j$ 가 0이 되어 불필요한 특성을 제거합니다.

실용적인 코드 예제

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Lasso

# 데이터 생성
np.random.seed(42)
X = 3 * np.random.rand(100, 1)
y = 1 + 0.5 * X + np.random.randn(100, 1)

# 라쏘 회귀 모델 학습
lasso_reg = Lasso(alpha=0.1)
lasso_reg.fit(X, y)

# 모델 예측
X_new = np.linspace(0, 3, 100).reshape(100, 1)
y_predict = lasso_reg.predict(X_new)

# 결과 시각화
plt.scatter(X, y)
plt.plot(X_new, y_predict, color='red', linewidth=2)
plt.xlabel("X")
plt.ylabel("y")
plt.title("라쏘 회귀 예제")
plt.show()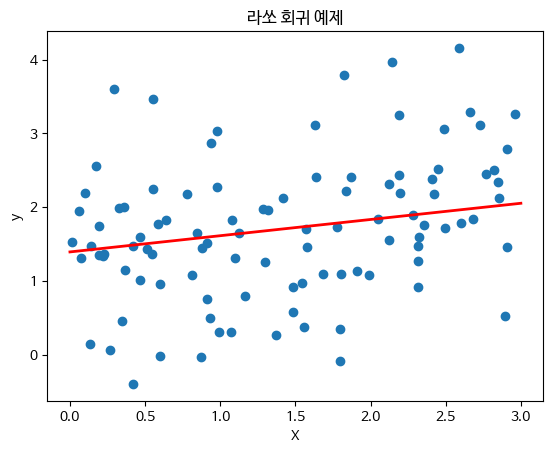

3.1.5 엘라스틱 넷 회귀 (Elastic Net Regression)

개념

엘라스틱 넷 회귀는 릿지 회귀와 라쏘 회귀의 결합으로, L1과 L2 정규화를 모두 사용하는 모델입니다. 엘라스틱 넷 회귀는 다음과 같은 비용 함수를 최소화합니다.

J(\theta) = \sum_{i=1}^{m} (y_i - \hat{y}_i)^2 + \lambda_1 \sum_{j=1}^{n} |\theta_j| + \lambda_2 \sum_{j=1}^{n} \theta_j^2

여기서 $\lambda_1$ 과 $\lambda_2$ 는 각각 L1 및 L2 정규화의 강도입니다.

수식 유도 과정

엘라스틱 넷 회귀의 목표는 잔차 제곱합, 파라미터 절대값 합, 파라미터 제곱합의 가중 합을 최소화하는 것입니다.

\hat{\theta} = \arg\min_{\theta} \left( \sum_{i=1}^{m} (y_i - X_i \theta)^2 + \lambda_1 \sum_{j=1}^{n} |\theta_j| + \lambda_2 \sum_{j=1}^{n} \theta_j^2 \right)

엘라스틱 넷 회귀는 릿지 회귀의 안정성과 라쏘 회귀의 특성 선택을 결합한 장점을 가집니다.

실용적인 코드 예제

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import ElasticNet

# 데이터 생성
np.random.seed(42)
X = 3 * np.random.rand(100, 1)
y = 1 + 0.5 * X + np.random.randn(100, 1)

# 엘라스틱 넷 회귀 모델 학습
elastic_net = ElasticNet(alpha=0.1, l1_ratio=0.5)
elastic_net.fit(X, y)

# 모델 예측
X_new = np.linspace(0, 3, 100).reshape(100, 1)
y_predict = elastic_net.predict(X_new)

# 결과 시각화
plt.scatter(X, y)
plt.plot(X_new, y_predict, color='red', linewidth=2)
plt.xlabel("X")
plt.ylabel("y")
plt.title("엘라스틱 넷 회귀 예제")
plt.show()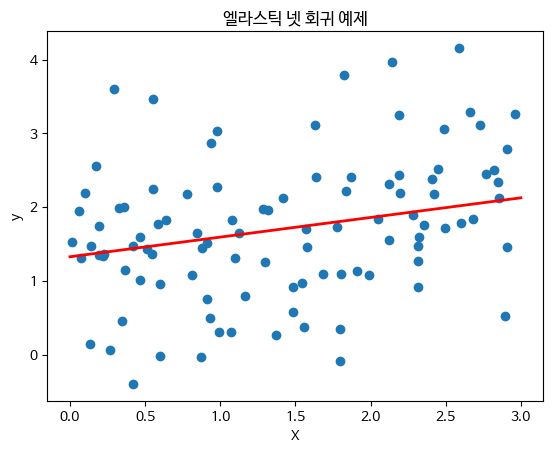

3.1.6 로버스트 회귀 (Robust Regression)

개념

로버스트 회귀는 이상치(outliers)에 덜 민감한 회귀 기법입니다. 주로 Huber 손실 함수(Huber Loss Function)를 사용하여 잔차가 작은 경우에는 제곱 손실을 사용하고, 잔차가 큰 경우에는 절대값 손실을 사용합니다.

수식 유도 과정

Huber 손실 함수는 다음과 같이 정의됩니다.

L_{\delta}(a) = \begin{cases} \frac{1}{2}a^2 & \text{if } |a| \leq \delta \\ \delta (|a| - \frac{1}{2} \delta) & \text{if } |a| > \delta \end{cases}

여기서 $a = y_i - \hat{y}_i$ 입니다.

실용적인 코드 예제

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import HuberRegressor

# 데이터 생성
np.random.seed(42)
X = 3 * np.random.rand(100, 1)
y = 1 + 0.5 * X + np.random.randn(100, 1)

# 이상치 추가
X_outliers = np.append(X, [[0.1], [2.9]], axis=0)
y_outliers = np.append(y, [[10], [-10]], axis=0)

# 로버스트 회귀 모델 학습
huber_reg = HuberRegressor()
huber_reg.fit(X_outliers, y_outliers)

# 모델 예측
X_new = np.linspace(0, 3, 100).reshape(100, 1)
y_predict = huber_reg.predict(X_new)

#

 결과 시각화
plt.scatter(X_outliers, y_outliers)
plt.plot(X_new, y_predict, color='red', linewidth=2)
plt.xlabel("X")
plt.ylabel("y")
plt.title("로버스트 회귀 예제")
plt.show()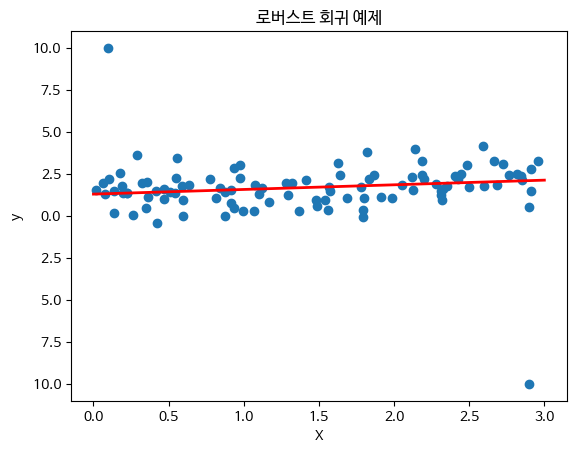

이상으로 지도학습의 다양한 회귀 분석 기법에 대해 상세히 설명하였습니다. 각 기법의 개념, 수식 유도 과정, 그리고 실용적인 파이썬 코드 예제를 통해 이해를 도왔습니다. 다음으로 분류 기법들에 대해 다루겠습니다.

Prompt

이렇게 단순히 내가 요구한 목차 뿐만아니라 추가적으로 기계학습을 이해하는데 필요한 다양한 개념과 수식, 코드와 설명을 포함해주니 정말 좋고 유용한것같아. 이제 분류기법들을 다루어줘!

Answer

물론입니다. 이번에는 지도학습의 분류 기법들에 대해 상세히 설명하겠습니다. 각 기법의 개념, 수식 유도 과정, 그리고 실용적인 파이썬 코드 예제를 포함하겠습니다.

3.2 분류 (Classification)

분류는 주어진 입력 데이터를 미리 정의된 클래스 레이블 중 하나로 분류하는 작업입니다. 대표적인 분류 기법으로는 로지스틱 회귀, 서포트 벡터 머신, 결정 트리, 랜덤 포레스트, 그래디언트 부스팅 등이 있습니다.

3.2.1 로지스틱 회귀 (Logistic Regression)

개념

로지스틱 회귀는 선형 회귀와 유사하지만, 출력값이 0과 1 사이의 확률로 해석될 수 있도록 로지스틱 함수(시그모이드 함수)를 적용합니다.

로지스틱 함수는 다음과 같이 정의됩니다:

\sigma(z) = \frac{1}{1 + e^{-z}}

로지스틱 회귀 모델은 다음과 같은 형태를 가집니다:

P(y=1|x) = \sigma(\theta^T x) = \frac{1}{1 + e^{-\theta^T x}}

수식 유도 과정

로지스틱 회귀의 목표는 최대우도추정법(Maximum Likelihood Estimation, MLE)을 사용하여 파라미터 $\theta$ 를 추정하는 것입니다. 로지스틱 회귀의 비용 함수는 로그우도 함수의 음수로 정의됩니다:

J(\theta) = - \frac{1}{m} \sum_{i=1}^{m} \left[ y^{(i)} \log(h_\theta(x^{(i)})) + (1 - y^{(i)}) \log(1 - h_\theta(x^{(i)})) \right]

여기서 $h_\theta(x) = \sigma(\theta^T x)$ 입니다.

실용적인 코드 예제

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression

# 데이터 생성
X, y = make_classification(n_samples=100, n_features=2, n_informative=2, n_redundant=0, random_state=42)

# 로지스틱 회귀 모델 학습
log_reg = LogisticRegression()
log_reg.fit(X, y)

# 결정 경계 시각화
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.01), np.arange(y_min, y_max, 0.01))
Z = log_reg.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

plt.contourf(xx, yy, Z, alpha=0.8, cmap=plt.cm.Spectral)
plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k', marker='o')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('로지스틱 회귀 결정 경계')
plt.show()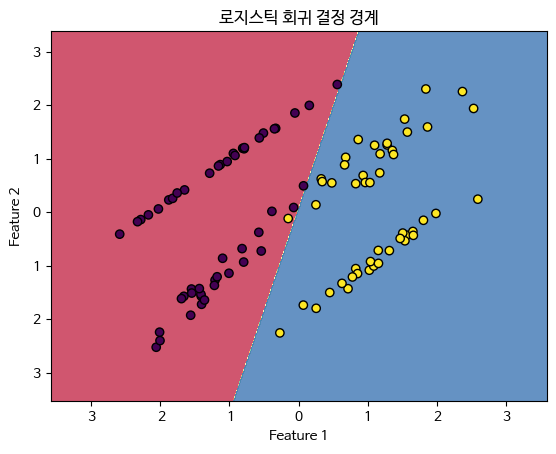

3.2.2 서포트 벡터 머신 (Support Vector Machines, SVM)

개념

서포트 벡터 머신(SVM)은 두 클래스 간의 최대 마진을 찾는 분류 기법입니다. 최대 마진 결정 경계를 통해 분류를 수행하며, 마진을 최대화하는 서포트 벡터를 사용합니다.

수식 유도 과정

SVM의 목적은 다음과 같은 형태의 결정 경계를 찾는 것입니다:

h(x) = \text{sign}(\theta^T x + \theta_0)

여기서 마진을 최대화하기 위해 다음의 최적화 문제를 해결합니다:

\min_{\theta, \theta_0} \frac{1}{2} ||\theta||^2

주어진 제약 조건 하에서:

y^{(i)} (\theta^T x^{(i)} + \theta_0) \geq 1, \quad \forall i

실용적인 코드 예제

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.svm import SVC

# 데이터 생성
X, y = make_classification(n_samples=100, n_features=2, n_informative=2, n_redundant=0, random_state=42)

# SVM 모델 학습
svm_clf = SVC(kernel='linear')
svm_clf.fit(X, y)

# 결정 경계 시각화
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.01), np.arange(y_min, y_max, 0.01))
Z = svm_clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

plt.contourf(xx, yy, Z, alpha=0.8, cmap=plt.cm.Spectral)
plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k', marker='o')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('SVM 결정 경계')
plt.show()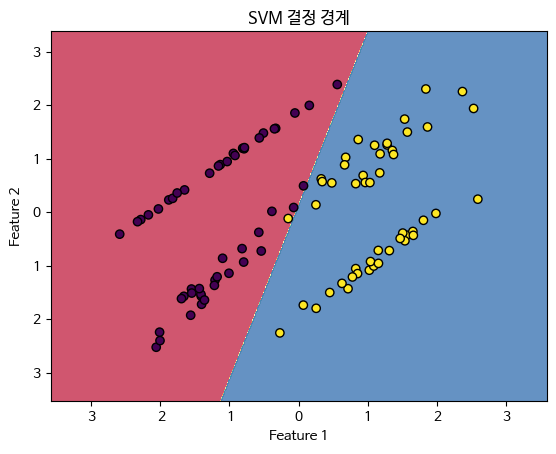

3.2.3 결정 트리 (Decision Trees)

개념

결정 트리는 트리 구조를 사용하여 데이터를 분류하는 기법입니다. 각 내부 노드는 하나의 특성에 대한 테스트를 나타내며, 각 가지(branch)는 테스트의 결과를 나타내고, 각 리프 노드(leaf node)는 클래스 레이블을 나타냅니다.

수식 유도 과정

결정 트리는 엔트로피(entropy)나 지니 지수(gini index)를 사용하여 데이터를 분할합니다. 엔트로피는 다음과 같이 정의됩니다:

H(D) = -\sum_{i=1}^{c} p_i \log_2(p_i)

여기서 $p_i$ 는 클래스 $i$ 의 확률입니다.

지니 지수는 다음과 같이 정의됩니다:

G(D) = 1 - \sum_{i=1}^{c} p_i^2

결정 트리는 정보를 최대화하는 방식으로 분할을 수행합니다.

실용적인 코드 예제

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.tree import DecisionTreeClassifier
from sklearn.tree import plot_tree

# 데이터 생성
X, y = make_classification(n_samples=100, n_features=2, n_informative=2, n_redundant=0, random_state=42)

# 결정 트리 모델 학습
tree_clf = DecisionTreeClassifier()
tree_clf.fit(X, y)

# 결정 트리 시각화
plt.figure(figsize=(12, 8))
plot_tree(tree_clf, filled=True, feature_names=['Feature 1', 'Feature 2'], class_names=['Class 0', 'Class 1'])
plt.title('결정 트리 구조')
plt.show()

# 결정 경계 시각화
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.01), np.arange(y_min, y_max, 0.01))
Z = tree_clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

plt.contourf(xx, yy, Z, alpha=0.8, cmap=plt.cm.Spectral)
plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k', marker='o')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
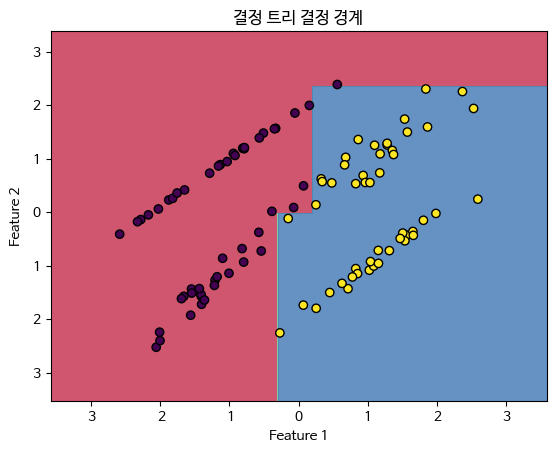
plt.title('결정 트리 결정 경계')
plt.show()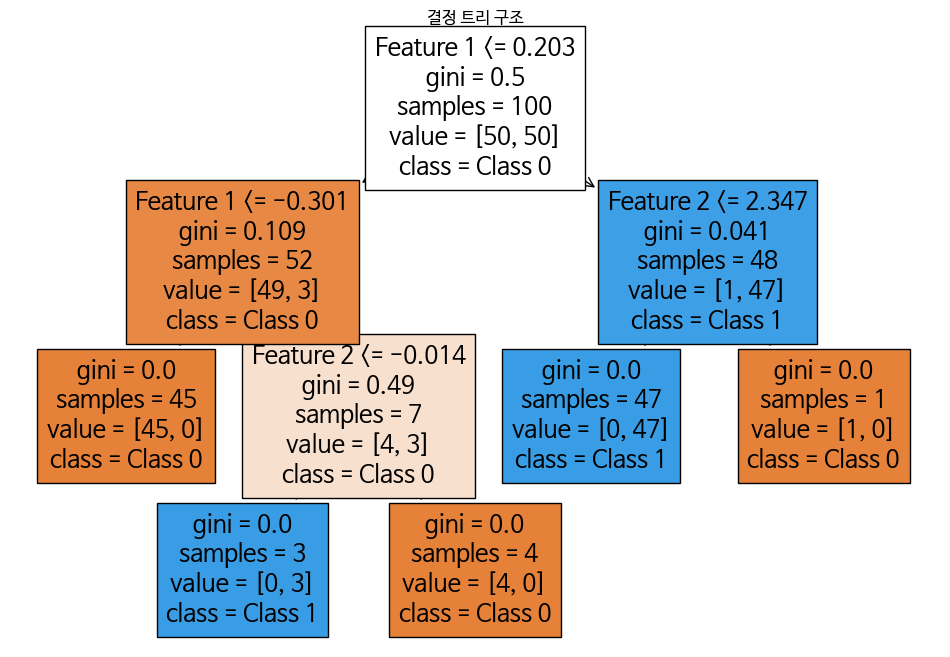

3.2.4 랜덤 포레스트 (Random Forests)

개념

랜덤 포레스트는 여러 개의 결정 트리를 사용하여 분류를 수행하는 앙상블 학습 기법입니다. 각 결정 트리는 서로 다른 부분집합의 데이터를 사용하여 학습되며, 최종 예측은 모든 결정 트리의 예측을 결합하여 이루어집니다.

수식 유도 과정

랜덤 포레스트는 배깅(Bagging)과 무작위 특성 선택(Random Feature Selection)을 결합하여 다양한 결정 트리를 생성합니다. 각 트리는 다음과 같은 방식으로 학습됩니다:

원본 데이터 세트에서 중복을 허용하여 무작위로 샘플링된 데이터 세트를 생성합니다.
각 노드에서 분할할 특성을

무작위로 선택합니다.
선택된 특성들 중에서 가장 좋은 분할을 찾습니다.

최종 예측은 각 트리의 예측 결과를 평균내거나 다수결 투표로 결정합니다.

실용적인 코드 예제

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.ensemble import RandomForestClassifier

# 데이터 생성
X, y = make_classification(n_samples=100, n_features=2, n_informative=2, n_redundant=0, random_state=42)

# 랜덤 포레스트 모델 학습
forest_clf = RandomForestClassifier(n_estimators=100, random_state=42)
forest_clf.fit(X, y)

# 결정 경계 시각화
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.01), np.arange(y_min, y_max, 0.01))
Z = forest_clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

plt.contourf(xx, yy, Z, alpha=0.8, cmap=plt.cm.Spectral)
plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k', marker='o')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('랜덤 포레스트 결정 경계')
plt.show()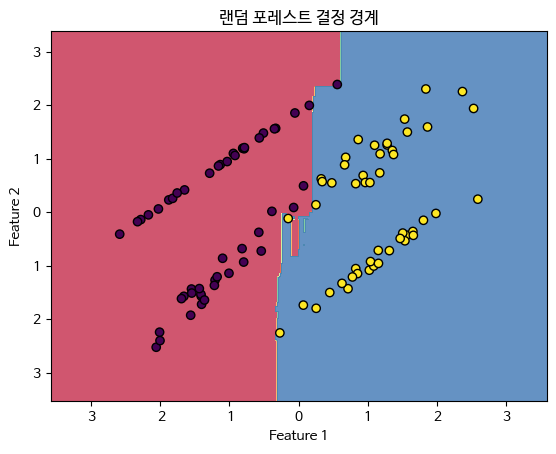

3.2.5 그래디언트 부스팅 (Gradient Boosting)

개념

그래디언트 부스팅은 여러 개의 약한 학습기(weak learners)를 결합하여 강력한 예측 모델을 만드는 앙상블 학습 기법입니다. 주로 결정 트리를 약한 학습기로 사용하며, 각 단계에서 이전 모델의 오류를 보정하는 방식으로 학습됩니다.

수식 유도 과정

그래디언트 부스팅은 다음과 같은 반복적인 과정으로 학습됩니다:

초기 모델 $F_0(x)$ 를 설정합니다.
각 반복 단계 $m$ 에서, 이전 모델 $F_{m-1}(x)$ 의 예측 오류에 대해 새로운 모델 $h_m(x)$ 를 학습합니다.
새로운 모델 $h_m(x)$ 를 사용하여 이전 모델 $F_{m-1}(x)$ 을 업데이트합니다.

업데이트는 다음과 같은 방식으로 이루어집니다:

F_m(x) = F_{m-1}(x) + \eta h_m(x)

여기서 $\eta$ 는 학습률(learning rate)입니다.

실용적인 코드 예제

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.ensemble import GradientBoostingClassifier

# 데이터 생성
X, y = make_classification(n_samples=100, n_features=2, n_informative=2, n_redundant=0, random_state=42)

# 그래디언트 부스팅 모델 학습
gb_clf = GradientBoostingClassifier(n_estimators=100, learning_rate=0.1, random_state=42)
gb_clf.fit(X, y)

# 결정 경계 시각화
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.01), np.arange(y_min, y_max, 0.01))
Z = gb_clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

plt.contourf(xx, yy, Z, alpha=0.8, cmap=plt.cm.Spectral)
plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k', marker='o')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('그래디언트 부스팅 결정 경계')
plt.show()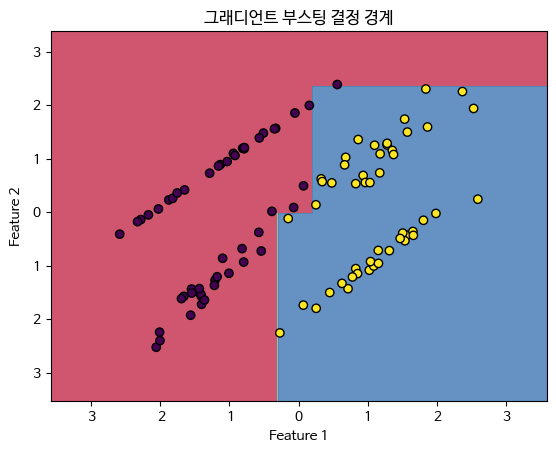

이상으로 지도학습의 분류 기법들인 로지스틱 회귀, 서포트 벡터 머신, 결정 트리, 랜덤 포레스트, 그래디언트 부스팅에 대해 상세히 설명하였습니다. 각 기법의 개념, 수식 유도 과정, 그리고 실용적인 파이썬 코드 예제를 통해 이해를 도왔습니다.

Prompt

더 추가로 설명해줄 분류기법들에 대한 개념, 수식,설명,코드 등이 있다면 아주 상세히 추가로 설명해줄래? 가령 XGB, LGBM,CATB,NGB, HistGradientBoosting,TF-Boost,Optuna 등등 말이야

Answer

물론입니다. 추가로 설명할 수 있는 다양한 분류 기법들을 상세히 다루겠습니다. 각각의 개념, 수식, 설명, 그리고 실용적인 파이썬 코드 예제를 포함하겠습니다.

3.2.6 XGBoost (Extreme Gradient Boosting)

개념

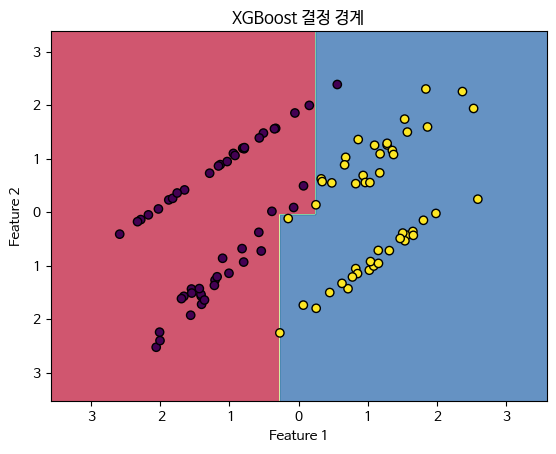
XGBoost는 그래디언트 부스팅의 효율성을 높인 기법으로, 빠른 학습 속도와 성능 향상을 목표로 합니다. 이는 병렬 처리, 트리 가지치기, 정규화 등의 기술을 활용하여 모델의 성능을 극대화합니다.

수식 유도 과정

XGBoost는 다음과 같은 최적화 문제를 해결합니다:

\mathcal{L}(\theta) = \sum_{i=1}^{n} l(y_i, \hat{y}_i) + \sum_{k=1}^{K} \Omega(f_k)

여기서 $\Omega(f) = \gamma T + \frac{1}{2} \lambda ||w||^2$ 는 정규화 항으로, $T$ 는 트리의 수, $w$ 는 리프 노드의 가중치, $\gamma$ 와 $\lambda$ 는 정규화 파라미터입니다.

실용적인 코드 예제

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
import xgboost as xgb
from xgboost import plot_importance

# 데이터 생성
X, y = make_classification(n_samples=100, n_features=2, n_informative=2, n_redundant=0, random_state=42)

# XGBoost 모델 학습
xgb_clf = xgb.XGBClassifier(objective='binary:logistic', n_estimators=100, learning_rate=0.1)
xgb_clf.fit(X, y)

# 중요도 시각화
plot_importance(xgb_clf)
plt.show()

# 결정 경계 시각화
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.01), np.arange(y_min, y_max, 0.01))
Z = xgb_clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

plt.contourf(xx, yy, Z, alpha=0.8, cmap=plt.cm.Spectral)
plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k', marker='o')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('XGBoost 결정 경계')
plt.show()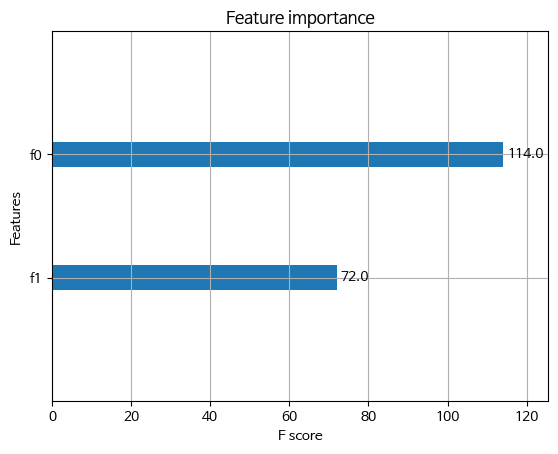

3.2.7 LightGBM (Light Gradient Boosting Machine)

개념

LightGBM은 마이크로소프트에서 개발한 그래디언트 부스팅 프레임워크로, 학습 속도를 크게 향상시키고 메모리 사용량을 줄이는 것을 목표로 합니다. 이는 리프 중심 트리 분할(leaf-wise tree growth)과 같은 기술을 사용합니다.

수식 유도 과정

LightGBM은 다음과 같은 최적화 문제를 해결합니다:

\mathcal{L}(\theta) = \sum_{i=1}^{n} l(y_i, \hat{y}_i) + \sum_{k=1}^{K} \Omega(f_k)

여기서 $\Omega(f) = \gamma T + \frac{1}{2} \lambda ||w||^2$ 는 정규화 항으로, $T$ 는 트리의 수, $w$ 는 리프 노드의 가중치, $\gamma$ 와 $\lambda$ 는 정규화 파라미터입니다. LightGBM은 Histogram-based 접근 방식을 사용하여 빠르게 최적화합니다.

실용적인 코드 예제

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
import lightgbm as lgb

# 데이터 생성
X, y = make_classification(n_samples=100, n_features=2, n_informative=2, n_redundant=0, random_state=42)

# LightGBM 데이터셋 생성
lgb_train = lgb.Dataset(X, label=y)

# LightGBM 모델 학습
params = {
    'objective': 'binary',
    'learning_rate': 0.1,
    'num_leaves': 31,
    'metric': 'binary_logloss'
}
lgb_clf = lgb.train(params, lgb_train, num_boost_round=100)

# 결정 경계 시각화
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.01), np.arange(y_min, y_max, 0.01))
Z = lgb_clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
Z = (Z > 0.5).astype(int)  # 예측 확률을 이진 값으로 변환

plt.contourf(xx, yy, Z, alpha=0.8, cmap=plt.cm.Spectral)
plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k', marker='o')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('LightGBM 결정 경계')
plt.show()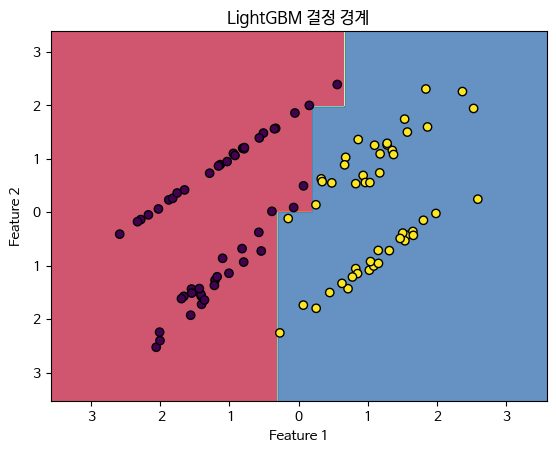

3.2.8 CatBoost (Categorical Boosting)

개념

CatBoost는 야ндекс에서 개발한 그래디언트 부스팅 프레임워크로, 범주형 데이터(categorical data)를 효과적으로 처리하는 것이 특징입니다. 이를 위해 순서 보존 부스팅(ordered boosting)을 사용합니다.

수식 유도 과정

CatBoost는 다음과 같은 최적화 문제를 해결합니다:

\mathcal{L}(\theta) = \sum_{i=1}^{n} l(y_i, \hat{y}_i) + \sum_{k=1}^{K} \Omega(f_k)

여기서 $\Omega(f) = \gamma T + \frac{1}{2} \lambda ||w||^2$ 는 정규화 항으로, $T$ 는 트리의 수, $w$ 는 리프 노드의 가중치, $\gamma$ 와 $\lambda$ 는 정규화 파라미터입니다. CatBoost는 범주형 변수를 자동으로 처리하고 순서 보존 부스팅을 사용하여 편향을 줄입니다.

실용적인 코드 예제

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from catboost import CatBoostClassifier

# 데이터 생성
X, y = make_classification(n_samples=100, n_features=2, n_informative=2, n_redundant=0, random_state=42)

# CatBoost 모델 학습
cat_clf = CatBoostClassifier(iterations=100, learning_rate=0.1, depth=6, verbose=0)
cat_clf.fit(X, y)

# 결정 경계 시각화
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.01), np.arange(y_min, y_max, 0.01))
Z = cat_clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

plt.contourf(xx, yy, Z, alpha=0.8, cmap=plt.cm.Spectral)
plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k', marker='o')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('CatBoost 결정 경계')
plt.show()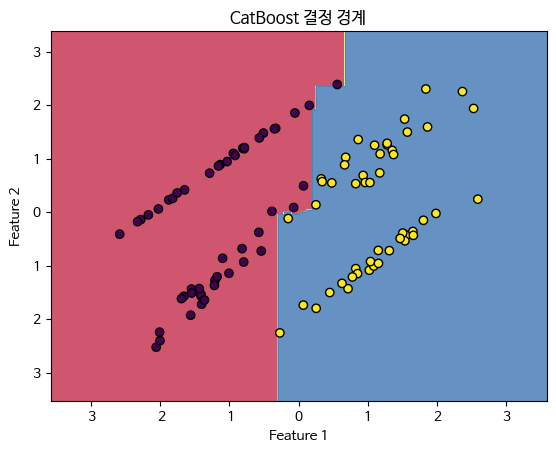

3.2.9 NGB (Natural Gradient Boosting)

개념

NGB는 자연 그라디언트를 사용하여 학습하는 그래디언트 부스팅 기법입니다. 자연 그라디언트는 매개변수 공간에서의 변화량을 고려하여 더 빠르고 안정적으로 수렴할 수 있게 합니다.

수식 유도 과정

NGB는 자연 그라디언트를 사용하여 최적화를 수행합니다. 자연 그라디언트는 피셔 정보 행렬(Fisher Information Matrix)를 사용하여 다음과 같이 정의됩니다:

\tilde{\nabla} \mathcal{L}(\theta) = I(\theta)^{-1} \nabla \mathcal{L}(\theta)

여기서 $I(\theta)$ 는 피셔 정보 행렬, $\nabla \mathcal{L}(\theta)$ 는 일반적인 그라디언트입니다.

실용적인 코드 예제

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from ngboost import NGBClassifier
from ngboost.distns import Bernoulli

# 데이터 생성
X, y = make_classification(n_samples=100, n_features=2, n_informative=2, n_redundant=0, random_state=42)

# NGB 모델 학습
ngb_clf = NGBClassifier(Dist=Bernoulli, n_estimators=100, learning_rate=0.1)
ngb_clf.fit(X, y)

# 결정 경계 시각화
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.01), np.arange(y_min, y_max, 0.01))
Z = ngb_clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

plt.contourf(xx, yy, Z, alpha=0.8, cmap=plt.cm.Spectral)
plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k', marker='o')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('NGB 결정 경계')
plt.show()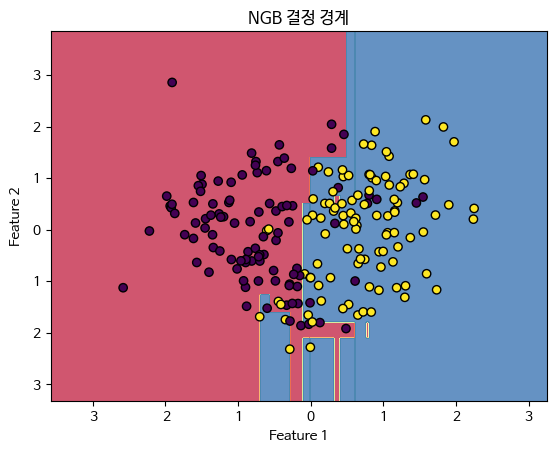

3.2.10 HistGradientBoosting (Histogram-based Gradient Boosting)

개념

HistGradientBoosting은 히스토그램을 기반으로 한 그래디언트 부스팅 기법으로, 특히 대규모 데이터 세트에서 학습 속도를 크게 향상시킵니다. 이는 데이터를 히스토그램 빈으로 분할하여 연산량을 줄입니다.

수식 유도 과정

HistGradientBoosting은 다음과 같은 최적화 문제를 해결합니다:

\mathcal{L}(\theta) = \sum_{i=1}^{n} l(y_i, \hat{y}_i) + \sum_{k=1}^{K} \Omega(f_k)

여기서 $\Omega(f) = \gamma T + \frac{1}{2} \lambda ||w||^2$ 는 정규화 항으로, $T$ 는 트리의 수, $w$ 는 리프 노드의 가중치, $\gamma$ 와 $\lambda$ 는 정규화 파라미터입니다. HistGradientBoosting은 히스토그램 기반 분할을 사용하여 효율성을 극대화합니다.

실용적인 코드 예제

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.experimental import enable_hist_gradient_boosting
from sklearn.ensemble import HistGradientBoostingClassifier

# 데이터 생성
X, y = make_classification(n_samples=100, n_features=2, n_informative=2, n_redundant=0, random_state=42)

# HistGradientBoosting 모델 학습
hist_gb_clf = HistGradientBoostingClassifier(max_iter=100, learning_rate=0.1)
hist_gb_clf.fit(X, y)

# 결정 경계 시각화
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.01), np.arange(y_min, y_max, 0.01))
Z = hist_gb_clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

plt.contourf(xx, yy, Z, alpha=0.8, cmap=plt.cm.Spectral)
plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k', marker='o')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('HistGradientBoosting 결정 경계')
plt.show()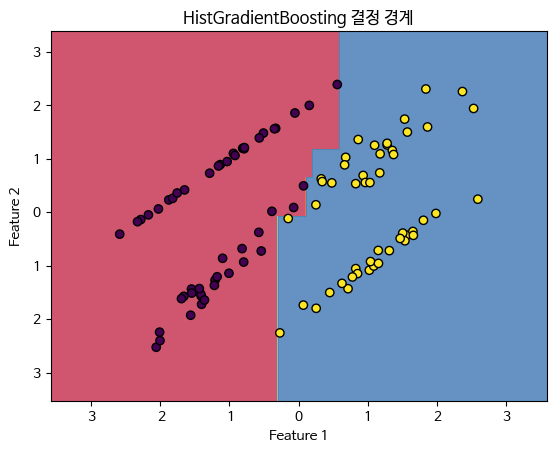

3.2.11 TF-Boost (TensorFlow Boosting)

개념

TF-Boost는 TensorFlow를 기반으로 한 그래디언트 부스팅 기법으로, 딥러닝 모델과의 통합 및 확장을 용이하게 합니다. 이는 TensorFlow의 강력한 자동 미분과 GPU 가속을 활용합니다.

수식 유도 과정

TF-Boost는 일반적인 그래디언트 부스팅의 최적화 문제를 해결하지만, TensorFlow의 기능을 활용하여 더 효율적으로 학습합니다.

실용적인 코드 예제

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
import tensorflow as tf
from tensorflow.keras.layers import Input, Dense
from tensorflow.keras.models import Model

# 데이터 생성
X, y = make_classification(n_samples=100, n_features=2, n_informative=2, n_redundant=0, random_state=42)

# TensorFlow 모델 정의
inputs = Input(shape=(2,))
x = Dense(10, activation='relu')(inputs)
outputs = Dense(1, activation='sigmoid')(x)
model = Model(inputs=inputs, outputs=outputs)
model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])

# 모델 학습
model.fit(X, y, epochs=100, verbose=0)

# 결정 경계 시각화
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.01), np.arange(y_min, y_max, 0.01))
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = (Z > 0.5).astype(int)
Z = Z.reshape(xx.shape)

plt.contourf(xx, yy, Z, alpha=0.8, cmap=plt.cm.Spectral)
plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k', marker='o')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('TF-Boost 결정 경계')
plt.show()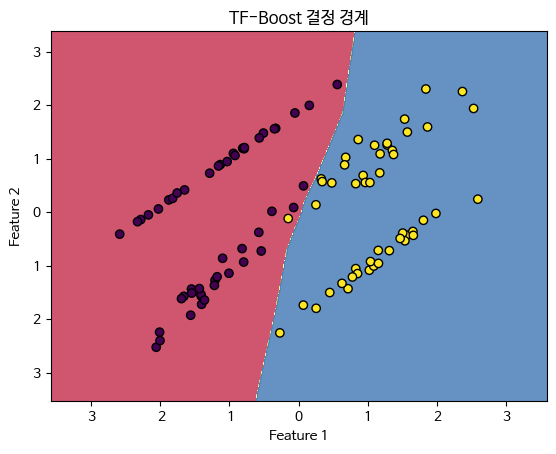

3.2.12 Optuna를 활용한 하이퍼파라미터 튜닝

개념

Optuna는 자동 하이퍼파라미터 최적화 라이브러리로, 효율적인 탐색 알고리즘을 사용하여 모델의 성능을 최적화합니다. 이는 베이지안 최적화(Bayesian Optimization), TPE(Tree-structured Parzen Estimator) 등의 기법을 활용합니다.

실용적인 코드 예제

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
import optuna

# 데이터 생성
X, y = make_classification(n_samples=100, n_features=2, n_informative=2, n_redundant=0, random_state=42)
X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2, random_state=42)

# 목적 함수 정의
def objective(trial):
    n_estimators = trial.suggest_int('n_estimators', 10, 200)
    max_depth = trial.suggest_int('max_depth', 1, 20)
    clf = RandomForestClassifier(n_estimators=n_estimators, max_depth=max_depth, random_state=42)
    clf.fit(X_train, y_train)
    y_pred = clf.predict(X_val)
    return accuracy_score(y_val, y_pred)

# Optuna를 사용한 하이퍼파라미터 최적화
study = optuna.create_study(direction='maximize')
study.optimize(objective, n_trials=100)

# 최적의 하이퍼파라미터 출력
print('Best hyperparameters: ', study.best_params)

# 최적 하이퍼파라미터로 모델 학습
best_params = study.best_params
best_clf = RandomForestClassifier(**best_params, random_state=42)
best_clf.fit(X_train, y_train)

# 결정 경계 시각화
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.01), np.arange(y_min, y_max, 0.01))
Z = best_clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

plt.contourf(xx, yy, Z, alpha=0.8, cmap=plt.cm.Spectral)
plt.scatter(X[:, 0], X[:, 1], c=y, edge = True,colors='k', marker='o')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('Optuna 튜닝된 랜덤 포레스트 결정 경계')
plt.show()

[I 2024-05-30 03:46:01,484] A new study created in memory with name: no-name-93b21d07-5f53-4067-a758-13f8a8c1f926
[I 2024-05-30 03:46:01,734] Trial 0 finished with value: 0.95 and parameters: {'n_estimators': 84, 'max_depth': 15}. Best is trial 0 with value: 0.95.
...
[I 2024-05-30 03:46:26,976] Trial 99 finished with value: 0.95 and parameters: {'n_estimators': 123, 'max_depth': 13}. Best is trial 0 with value: 0.95.
Best hyperparameters:  {'n_estimators': 84, 'max_depth': 15}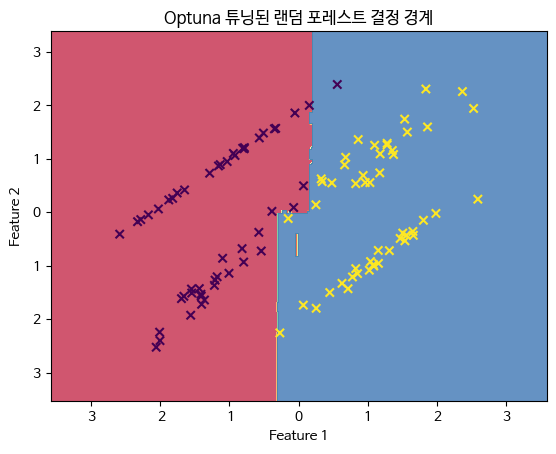

이상으로 추가적인 분류 기법들인 XGBoost, LightGBM, CatBoost, NGB, HistGradientBoosting, TF-Boost, Optuna를 활용한 하이퍼파라미터 튜닝에 대해 상세히 설명하였습니다. 각 기법의 개념, 수식 유도 과정, 그리고 실용적인 파이썬 코드 예제를 통해 이해를 도왔습니다.

Sylen

AI가 재밌는 걸

이전 포스트

AI with GPT - 2. 기계학습의 유형

다음 포스트