[Upstage AI Lab 3기] ML 프로젝트 기본 이론 : Deep Learning & Pytorch

Sylen·2024년 6월 20일
UpstageAILab국비지원업스테이지패스트캠퍼스패스트캠퍼스패스트캠퍼스AI부트캠프패스트캠퍼스업스테이지부트캠프패스트캠퍼스업스테이지에이아이랩

Upstage AI Lab 3기

목록 보기
7/19

파이토치와 딥러닝 과목에 들어서면서 이제 본격적으로 인공지능 공부를 시작하게 되었다. 업스테이지의 이활석 CTO님이 직접 진행하는 딥러닝 강의를 들을 수 있었는데 확실히 매우 유익하고 딥러닝에 대한 개념을 수학적으로도 배울 수 있어 정말 좋았다.
딥러닝 및 파이토치를 공부하면서 개인적으로 관심이 갔던 것이 Nomalization이었는데, batch nomalization과 layer nomalization을 비롯해서 다양한 정규화 기법들을 공부하고 넘파이를 활용한 코드 실습도 진행할 수 있었다.
이런 정규화 기법을 좀 더 직관적으로 이해해보고, 또 다른 정규화기법은 무엇이 있는지 알아보면서 스터디원들과 공유하는 시간을 갖게 되었는데 이 내용을 블로그에도 공유하고자 한다.

Nomalization

딥러닝 학습 시 안정성을 향상시키기 위해 데이터와 입출력을 밸런싱하는 과정이라고 설명할 수 있습니다. 이들 기술은 학습의 효율성과 성능을 높이는 데 중요한 역할

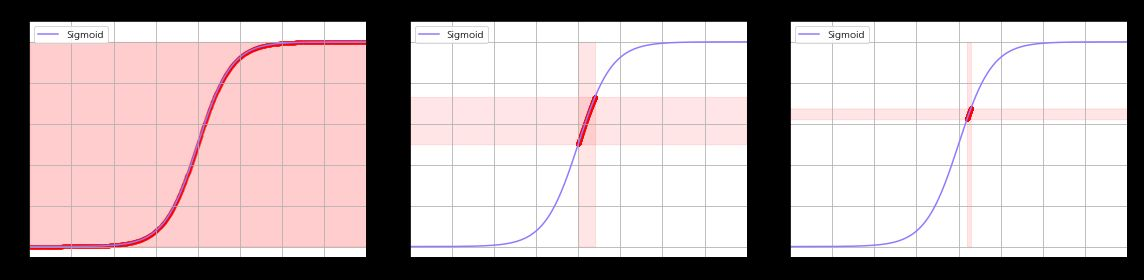
데이터 입출력시 실제로 정규화가 어떻게 적영되는지에 대해 의문

GPT 활용

🗨️ 활성화함수로 시그모이드를 사용했을때 발생할 수 있는 그래디언트 배니싱문제를 배치 정규화로 해결할수있다고 하는데, 맞니? 그런데 배치 정규화가 뭐고 그게 어떻게 적용되길래 그런 결과가 나오는지 **실제적**이고 **구체적**이고 **직관적**이게 알려줄래? 파이썬 **코드와 수식** 및 사례 기반의 상세한 설명도 좋아

배치 정규화를 넘파이로 직접 구현하여 직관적으로 확인해보겠습니다. 배치 정규화의 주요 단계를 하나씩 구현해보겠습니다.

1. 데이터 생성 및 초기화

먼저 임의의 데이터와 모델 파라미터를 초기화합니다.

import numpy as np

# 임의의 데이터 생성
np.random.seed(0)
X = np.random.rand(100, 20)

# 모델 파라미터 초기화
W = np.random.randn(20, 64)
b = np.random.randn(64)

# 시그모이드 활성화 함수
def sigmoid(x):
    return 1 / (1 + np.exp(-x))

2. 순전파: 배치 정규화 없이

배치 정규화 없이 단순한 순전파 과정을 수행합니다.

# 선형 변환
Z = np.dot(X, W) + b

# 시그모이드 활성화 함수 적용
A = sigmoid(Z)

print("Without Batch Normalization:")
print("Mean:", np.mean(A))
print("Variance:", np.var(A))

3. 배치 정규화 적용

배치 정규화 과정을 추가합니다.

# 배치 정규화 파라미터
gamma = np.ones(64)
beta = np.zeros(64)
epsilon = 1e-8

# 배치의 평균과 분산 계산
mu = np.mean(Z, axis=0)
sigma2 = np.var(Z, axis=0)

# 정규화
Z_normalized = (Z - mu) / np.sqrt(sigma2 + epsilon)

# 스케일링과 시프트
Z_tilde = gamma * Z_normalized + beta

# 시그모이드 활성화 함수 적용
A_bn = sigmoid(Z_tilde)

print("With Batch Normalization:")
print("Mean:", np.mean(A_bn))
print("Variance:", np.var(A_bn))

이 코드에서는 배치 정규화를 적용하기 전후의 활성화 값들의 평균과 분산을 비교할 수 있습니다. 배치 정규화를 통해 각 배치의 입력값이 정규화되고, 활성화 함수 적용 후에도 적절한 분포를 유지하는 것을 확인할 수 있습니다.

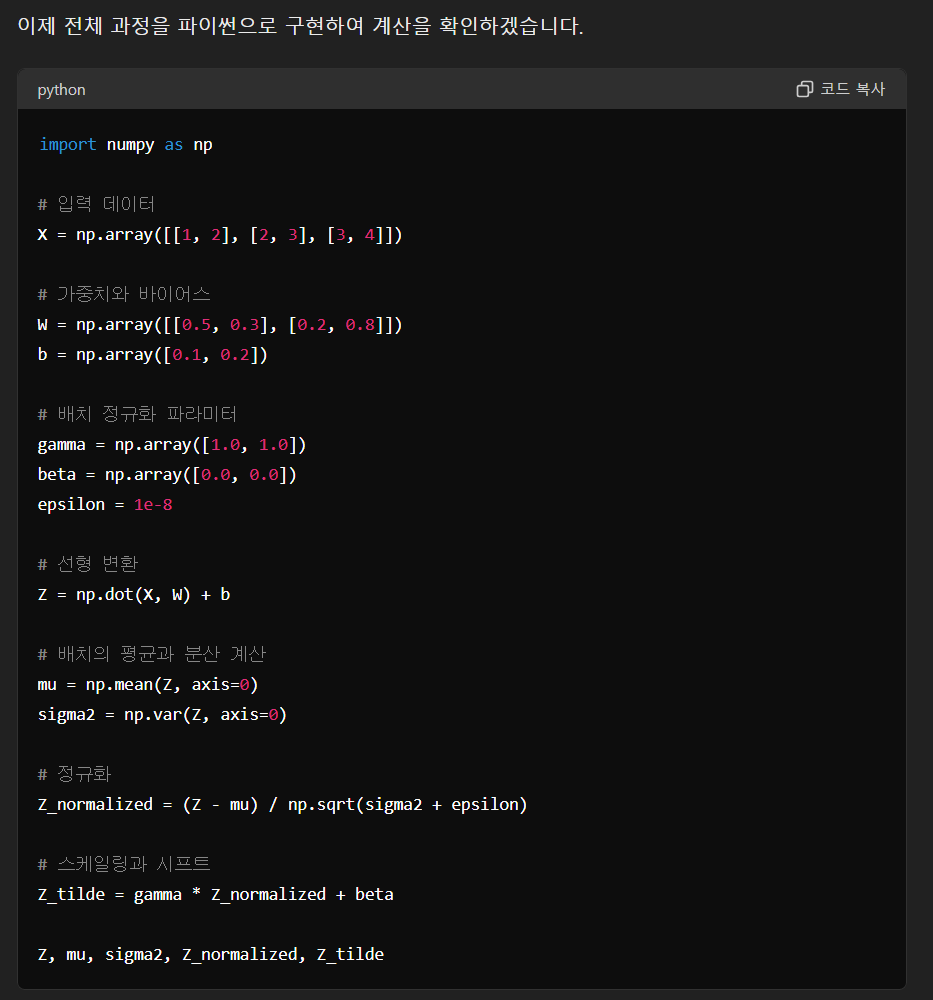
4. 전체 과정

전체 과정을 한 번에 정리해 보겠습니다.

import numpy as np

# 임의의 데이터 생성
np.random.seed(0)
X = np.random.rand(100, 20)

# 모델 파라미터 초기화
W = np.random.randn(20, 64)
b = np.random.randn(64)

# 시그모이드 활성화 함수
def sigmoid(x):
    return 1 / (1 + np.exp(-x))

# 선형 변환
Z = np.dot(X, W) + b

# 시그모이드 활성화 함수 적용
A = sigmoid(Z)

print("Without Batch Normalization:")
print("Mean:", np.mean(A))
print("Variance:", np.var(A))

# 배치 정규화 파라미터
gamma = np.ones(64)
beta = np.zeros(64)
epsilon = 1e-8

# 배치의 평균과 분산 계산
mu = np.mean(Z, axis=0)
sigma2 = np.var(Z, axis=0)

# 정규화
Z_normalized = (Z - mu) / np.sqrt(sigma2 + epsilon)

# 스케일링과 시프트
Z_tilde = gamma * Z_normalized + beta

# 시그모이드 활성화 함수 적용
A_bn = sigmoid(Z_tilde)

print("With Batch Normalization:")
print("Mean:", np.mean(A_bn))
print("Variance:", np.var(A_bn))

이 코드를 실행하면 배치 정규화 전후의 활성화 값들의 평균과 분산이 출력됩니다. 배치 정규화를 적용한 경우, 활성화 값들이 평균 0과 분산 1에 가까워지는 것을 확인할 수 있습니다. 이는 배치 정규화를 통해 입력 데이터의 분포를 조절함으로써 그래디언트 배니싱 문제를 완화하는 효과를 나타냅니다.

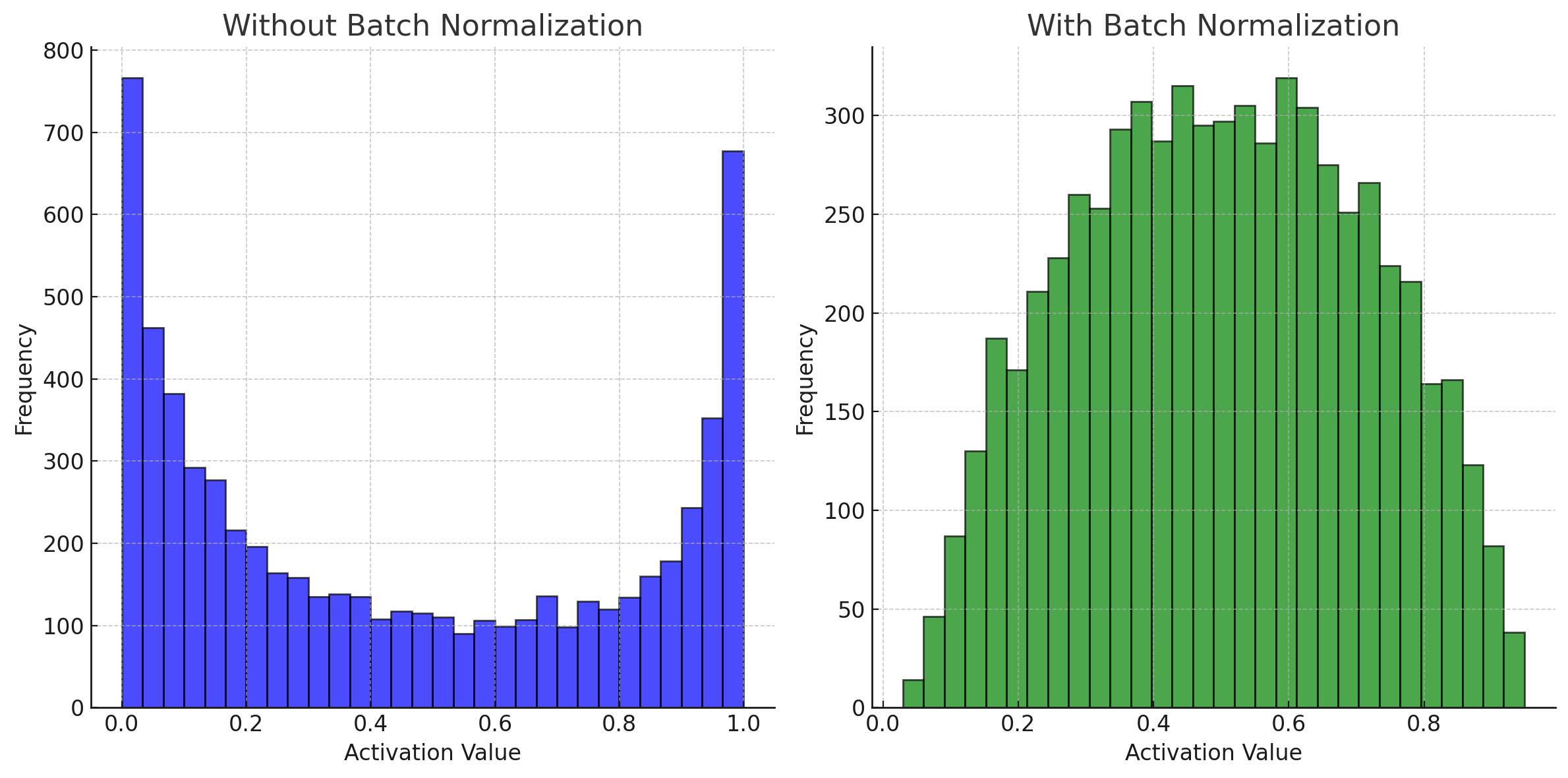
위 결과를 보면, 배치 정규화 적용 전후의 활성화 값들의 분포를 시각적으로 비교할 수 있습니다.

  • Without Batch Normalization:
    • 평균: 약 0.450
    • 분산: 약 0.130
  • With Batch Normalization:
    • 평균: 약 0.500
    • 분산: 약 0.044

배치 정규화를 적용한 경우, 활성화 값들이 더 집중된 분포를 가지며, 평균과 분산이 더 일정해지는 것을 확인할 수 있습니다. 이는 배치 정규화가 활성화 값들의 분포를 조절하여, 그래디언트 배니싱 문제를 완화하는 데 도움이 된다는 것을 시각적으로 보여줍니다.

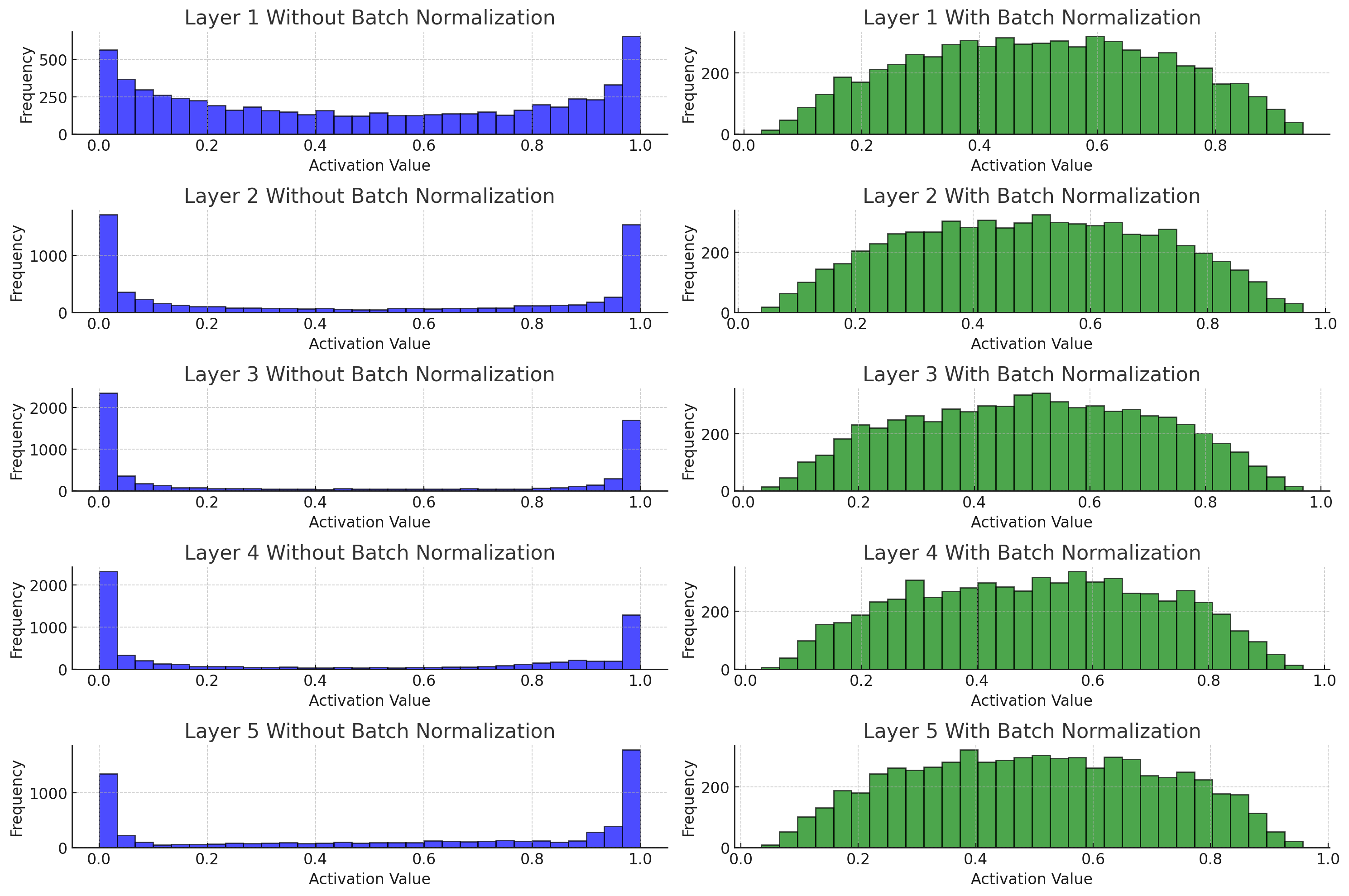
🗨️ 5개의 레이어를 통과했을때를 변화를 보고싶네 
# 임의의 데이터 생성
np.random.seed(0)
X = np.random.rand(100, 20)

# 모델 파라미터 초기화
layer_sizes = [20, 64, 64, 64, 64, 64]
Ws = [np.random.randn(layer_sizes[i], layer_sizes[i+1]) for i in range(len(layer_sizes)-1)]
bs = [np.random.randn(layer_sizes[i+1]) for i in range(len(layer_sizes)-1)]

# 시그모이드 활성화 함수
def sigmoid(x):
    return 1 / (1 + np.exp(-x))

# 배치 정규화 파라미터
gamma = np.ones(layer_sizes[-1])
beta = np.zeros(layer_sizes[-1])
epsilon = 1e-8

def forward_pass(X, Ws, bs, use_bn=False):
    A = X
    activations = []
    for i in range(len(Ws)):
        Z = np.dot(A, Ws[i]) + bs[i]
        if use_bn:
            mu = np.mean(Z, axis=0)
            sigma2 = np.var(Z, axis=0)
            Z = (Z - mu) / np.sqrt(sigma2 + epsilon)
            Z = gamma * Z + beta
        A = sigmoid(Z)
        activations.append(A)
    return activations

# 배치 정규화 없이 순전파
activations_no_bn = forward_pass(X, Ws, bs, use_bn=False)

# 배치 정규화와 함께 순전파
activations_bn = forward_pass(X, Ws, bs, use_bn=True)

# 시각화
plt.figure(figsize=(15, 10))

for i in range(5):
    plt.subplot(5, 2, 2*i + 1)
    plt.hist(activations_no_bn[i].flatten(), bins=30, alpha=0.7, color='blue', edgecolor='black')
    plt.title(f'Layer {i+1} Without Batch Normalization')
    plt.xlabel('Activation Value')
    plt.ylabel('Frequency')
    plt.grid(True)

    plt.subplot(5, 2, 2*i + 2)
    plt.hist(activations_bn[i].flatten(), bins=30, alpha=0.7, color='green', edgecolor='black')
    plt.title(f'Layer {i+1} With Batch Normalization')
    plt.xlabel('Activation Value')
    plt.ylabel('Frequency')
    plt.grid(True)

plt.tight_layout()
plt.show()

mean_var_no_bn = [(np.mean(act), np.var(act)) for act in activations_no_bn]
mean_var_bn = [(np.mean(act), np.var(act)) for act in activations_bn]

mean_var_no_bn, mean_var_bn

🗨️ 배치의 평균과 분산을 계산해서 정규화 및 스케일링, 시프트 하는 전체 과정에 대해서 실제 **예시**와 **수식**으로 보여줄 수있나? 계산이 어떻게 해서 정규화가 된건지 궁금하네. 아주 상세한 설명이 필요할것같아.

그 외 정규화 기법

🗨️ 요약 및 정리 ● 배치 정규화: 배치 단위로 학습시 발생할 수 있는 분포를 정규화하여 모델 학습을 안정화함 ● 레이어 정규화: 시계열 데이터와 같은 가변적인 입력에서 적용이 힘든 배치 정규화의 단점을 보완함 ● 인스턴스 정규화: 이미지 스타일 변환와 같이 각 데이터만의 고유한 정보를 유지할 때 이용 ● 그룹 정규화: 인스턴스 정규화의 확장 버전으로 배치 사이즈의 크기가 작아도 잘 동작하는 방법을 제안

이 밖에 또 알아야만 하는 정규화 기법이 추가로 뭐가 있을까?

정규화 기법은 신경망 학습의 안정화와 성능 향상에 중요한 역할을 합니다. 여기서 상황에 따른 다양한 정규화 기법에 대해 자세히 설명드리겠습니다.

배치 정규화 (Batch Normalization)

개념: 배치 단위로 평균과 분산을 계산하여 정규화합니다.

적용 상황: 대부분의 경우에 사용 가능하지만, 배치 크기가 작거나 RNN과 같이 배치 크기가 변동되는 경우에는 적합하지 않을 수 있습니다.

장점:

  • 학습 속도 증가
  • 그래디언트 배니싱 문제 완화
  • 과적합 방지 효과

단점:

  • 작은 배치 크기에서 성능 저하
  • RNN에서는 사용이 어렵다.

레이어 정규화 (Layer Normalization)

개념: 각 샘플의 모든 특징에 대해 평균과 분산을 계산하여 정규화합니다.

적용 상황: 배치 크기가 작거나 RNN과 같이 배치 크기가 변동되는 경우.

장점:

  • 배치 크기에 영향을 받지 않음
  • RNN에서 사용 가능

단점:

  • 배치 정규화에 비해 학습 속도가 느릴 수 있음

인스턴스 정규화 (Instance Normalization)

개념: 각 데이터 인스턴스에 대해 정규화합니다. 주로 컴퓨터 비전, 특히 스타일 변환 작업에서 사용됩니다.

적용 상황: 이미지 스타일 변환과 같은 경우에 사용.

장점:

  • 각 인스턴스의 고유한 특징을 유지하면서 정규화

단점:

  • 배치 크기에 따라 성능이 크게 변하지 않음

그룹 정규화 (Group Normalization)

개념: 인스턴스 정규화의 확장 버전으로, 채널을 여러 그룹으로 나누어 각 그룹 내에서 정규화합니다.

적용 상황: 배치 크기가 작거나 배치 정규화가 잘 동작하지 않는 경우.

장점:

  • 작은 배치 크기에서도 잘 동작
  • 다양한 네트워크 아키텍처에서 사용 가능

단점:

  • 하이퍼파라미터(그룹 수) 설정이 필요

층별 정규화 (Layer-wise Normalization)

개념: 각 레이어의 출력을 정규화하는 방법입니다. 레이어 전체의 평균과 분산을 계산하여 정규화합니다.

적용 상황: 배치 정규화나 레이어 정규화의 대안으로 사용.

장점:

  • 각 레이어의 출력 분포를 일정하게 유지

단점:

  • 계산 비용이 크고 구현이 복잡할 수 있음

https://paperswithcode.com/method/layer-normalization

Feature wise Nomarlization

https://www.sciencedirect.com/science/article/abs/pii/S0031320321004878

https://distill.pub/2018/feature-wise-transformations/

개념: 배치 내의 각 샘플에 대해 개별적으로 정규화합니다.

적용 상황: 배치 정규화의 대안으로 사용.

장점:

  • 각 샘플의 특징을 유지하면서 정규화

단점:

  • 샘플 간의 상호작용을 고려하지 않음

스펙트럴 정규화 (Spectral Normalization)

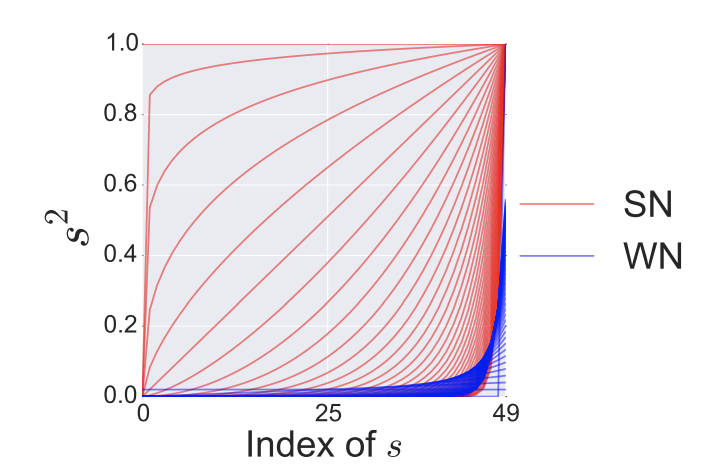
https://paperswithcode.com/method/spectral-normalization

개념: 각 레이어의 가중치 행렬의 스펙트럼(특히, 최대 특이값)을 정규화하여 학습을 안정화합니다. 주로 GAN에서 사용됩니다.

적용 상황: GAN의 안정적인 학습을 위해 사용.

장점:

  • GAN의 학습 안정성 향상
  • 모드 붕괴 문제 완화

단점:

  • 계산 비용이 크고 구현이 복잡할 수 있음

자기 정규화 신경망 (Self-Normalizing Neural Networks, SNN)

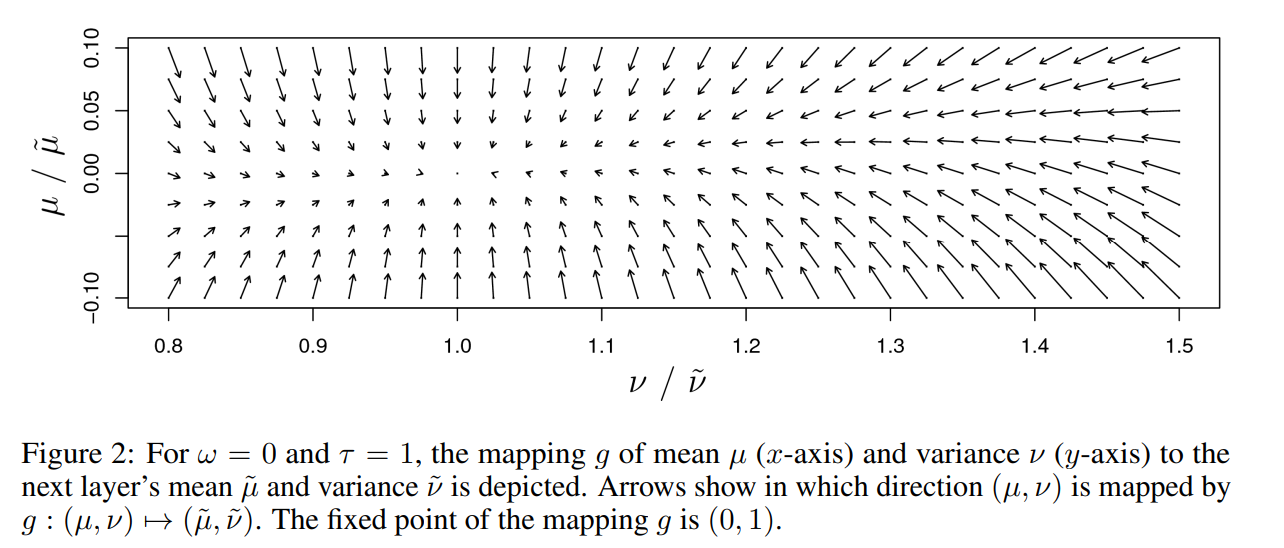
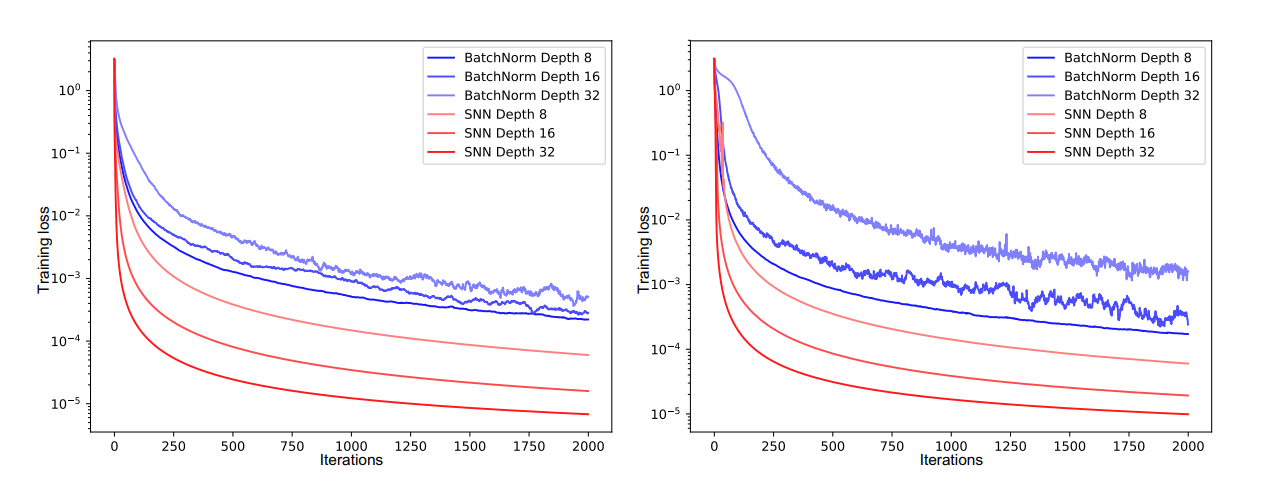
https://arxiv.org/abs/1706.02515

https://medium.com/@damoncivin/self-normalising-neural-networks-snn-2a972c1d421

개념: SELU(Scaled Exponential Linear Unit) 활성화 함수와 함께 사용되어 입력 데이터의 분포를 자체적으로 정규화합니다.

적용 상황: 신경망의 모든 층에서 정규화를 유지하려는 경우.

장점:

  • 별도의 정규화 층이 필요 없음
  • 학습 과정이 더 빠르고 안정적

단점:

  • 특정 활성화 함수(SELU)와 함께 사용해야 함

웨이트 정규화 (Weight Normalization)

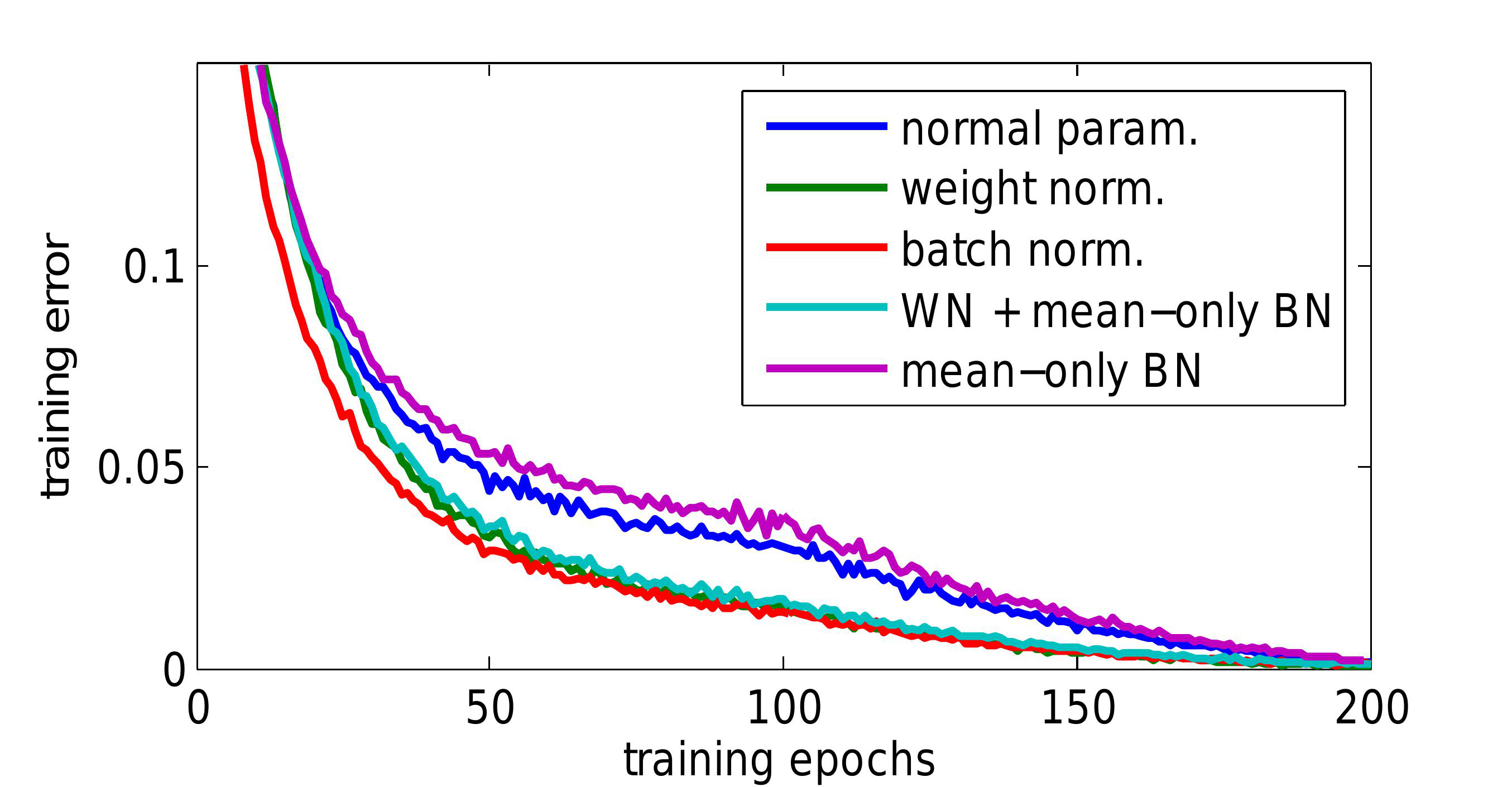
https://paperswithcode.com/method/weight-normalization

https://arxiv.org/abs/1602.07868

개념: 각 레이어의 가중치를 정규화하여 학습을 안정화합니다.

적용 상황: 모든 종류의 신경망에서 사용 가능.

장점:

  • 학습 속도 증가
  • 그래디언트 배니싱 문제 완화

단점:

  • 추가 계산 비용 발생

각 정규화 기법은 특정 상황에서 더 효과적일 수 있으며, 문제의 특성과 데이터의 특성에 맞게 적절히 선택하는 것이 중요합니다. 정규화 기법을 잘 이해하고, 필요에 따라 다양한 기법을 적용하여 최적의 성능을 얻는 것이 중요합니다.

https://paperswithcode.com/

Local Response Normalization 항목

Local Response Normalization 관련 코드 깃허브

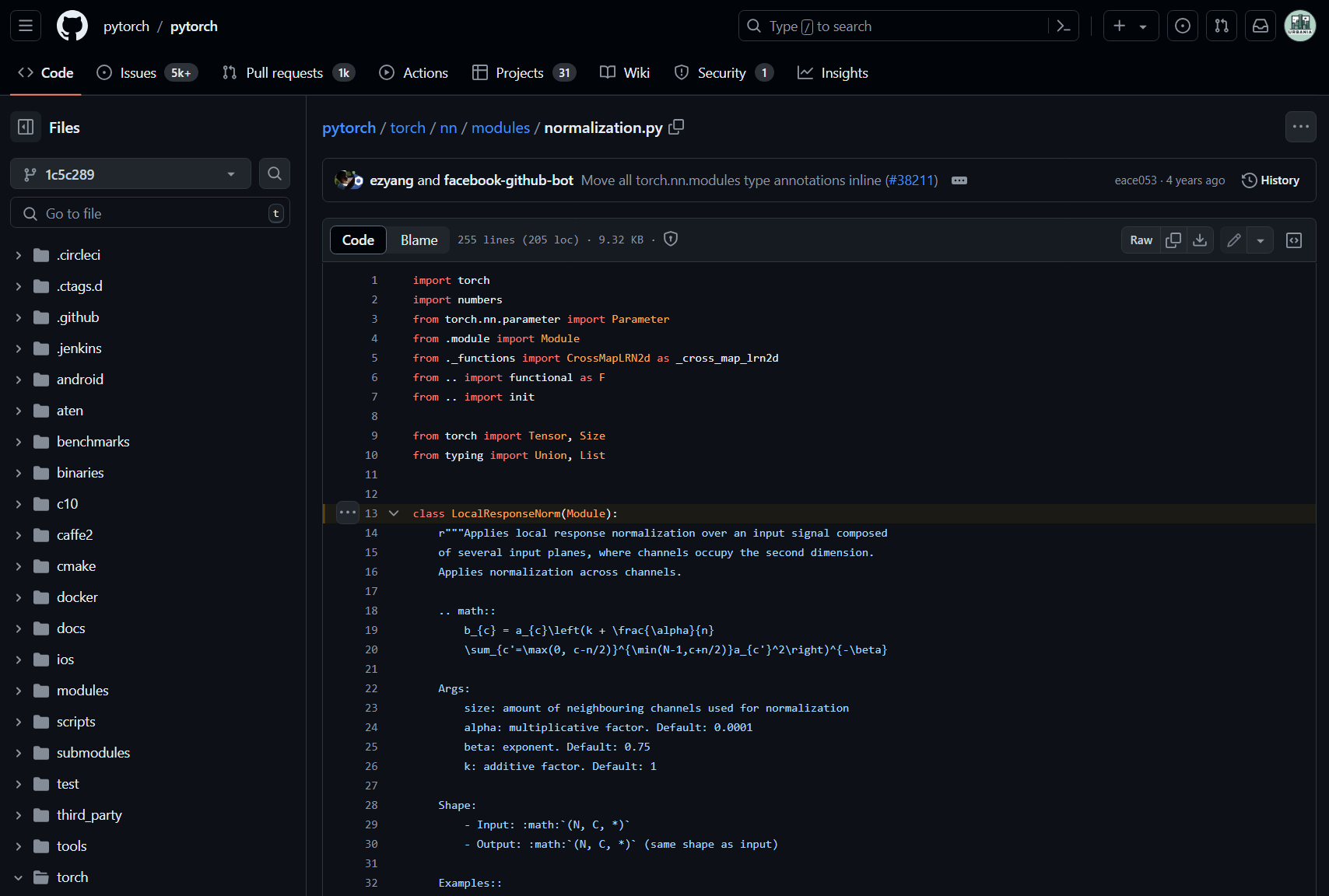
Local Response Normalization 논문

논문 | 코드 | paperswithcode의 설명을 함께 넣어 GPT에게 질문

🗨️ CNN에 적용 

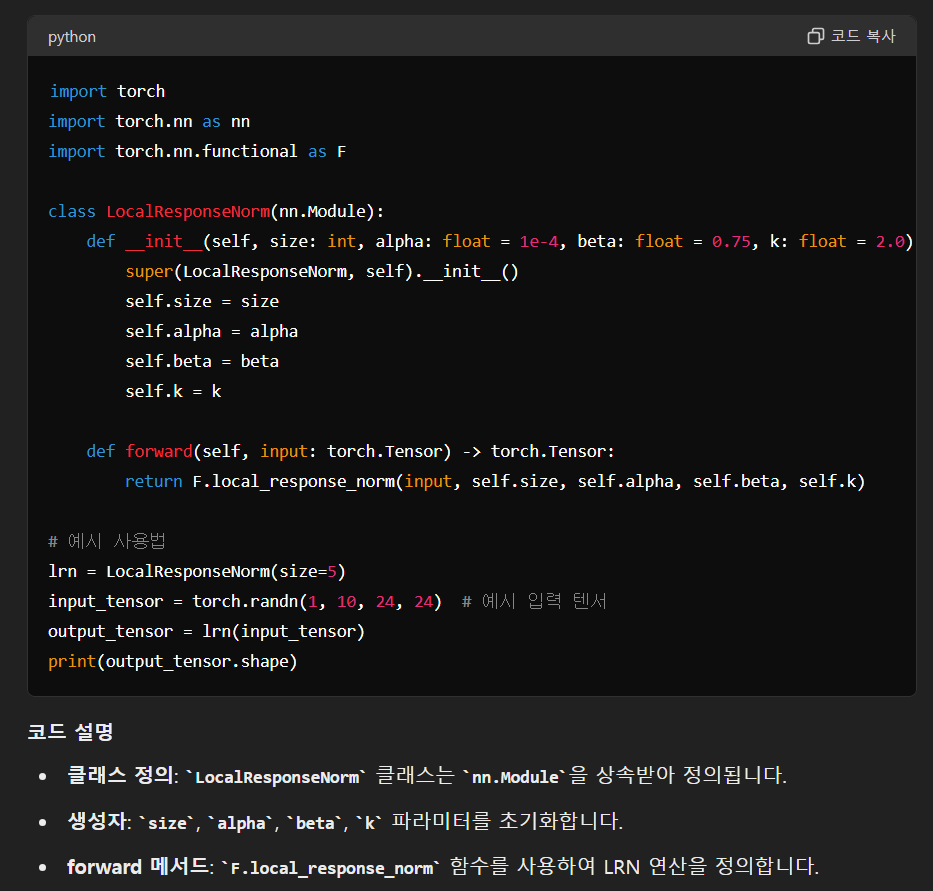
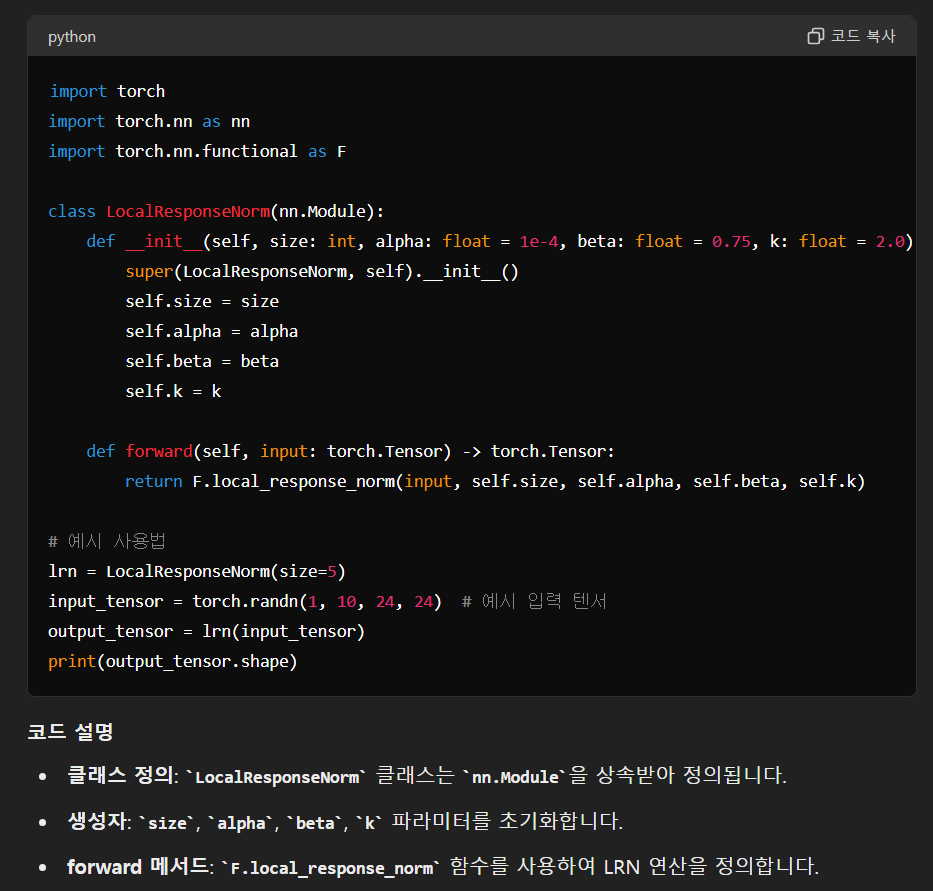
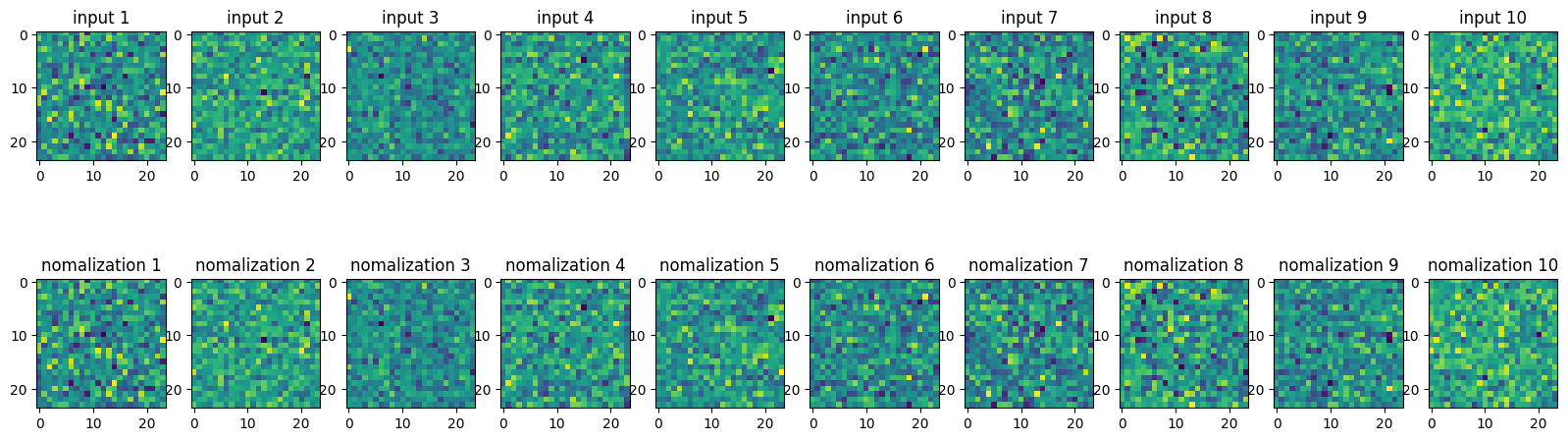
import torch
import torch.nn as nn
import torch.nn.functional as F

# Local Response Normalization class
class LocalResponseNorm(nn.Module):
    def __init__(self, size: int, alpha: float = 1e-4, beta: float = 0.75, k: float = 2.0):
        super(LocalResponseNorm, self).__init__()
        self.size = size
        self.alpha = alpha
        self.beta = beta
        self.k = k

    def forward(self, input: torch.Tensor) -> torch.Tensor:
        return F.local_response_norm(input, self.size, self.alpha, self.beta, self.k)

# CNN 모델 정의
class SimpleCNN(nn.Module):
    def __init__(self):
        super(SimpleCNN, self).__init__()
        self.conv1 = nn.Conv2d(in_channels=3, out_channels=32, kernel_size=3, padding=1)
        self.lrn1 = LocalResponseNorm(size=5)
        self.pool1 = nn.MaxPool2d(kernel_size=2, stride=2)
        
        self.conv2 = nn.Conv2d(in_channels=32, out_channels=64, kernel_size=3, padding=1)
        self.lrn2 = LocalResponseNorm(size=5)
        self.pool2 = nn.MaxPool2d(kernel_size=2, stride=2)

        # 새로운 컨볼루션 및 풀링 계층 추가
        self.conv3 = nn.Conv2d(in_channels=64, out_channels=128, kernel_size=3, padding=1)
        self.lrn3 = LocalResponseNorm(size=5)
        self.pool3 = nn.MaxPool2d(kernel_size=2, stride=2)
        
        self.fc1 = nn.Linear(128 * 4 * 4, 256)
        self.fc2 = nn.Linear(256, 10)
        
    def forward(self, x):
        x = self.pool1(F.relu(self.lrn1(self.conv1(x))))
        x = self.pool2(F.relu(self.lrn2(self.conv2(x))))
        
        # 새로운 계층의 순전파 단계
        x = self.pool3(F.relu(self.lrn3(self.conv3(x))))
        
        x = x.view(-1, 128 * 4 * 4)
        x = F.relu(self.fc1(x))
        x = self.fc2(x)
        return x

# 모델 인스턴스 생성 및 출력 확인
model = SimpleCNN()
print(model)

# 예시 입력 데이터 생성 및 모델 출력 확인
input_data = torch.randn(1, 3, 32, 32)  # 예시 입력 텐서 (1개 배치, 3채널, 32x32 크기)
output_data = model(input_data)
print(output_data.shape)

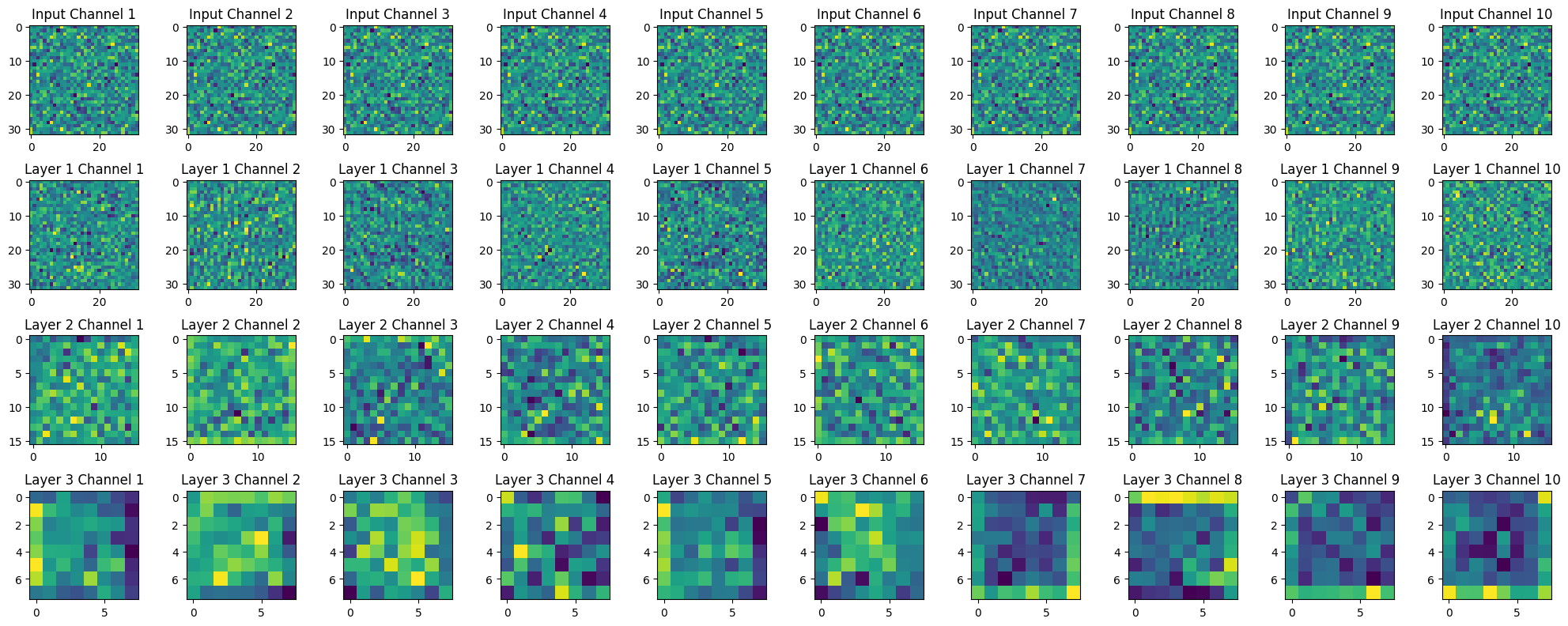
인사이트

1. 공부를 하다 코드 구현이나 수식에 대해 궁금하거나 추가적인 설명이 필요할 때

GPT에 간단한 수업 내용과 함께

전문적 | 상세한 | 친절한 키워드 고려

수식 | 코드 | 주석 | 해설 | 시각화 형태로 출력 요구

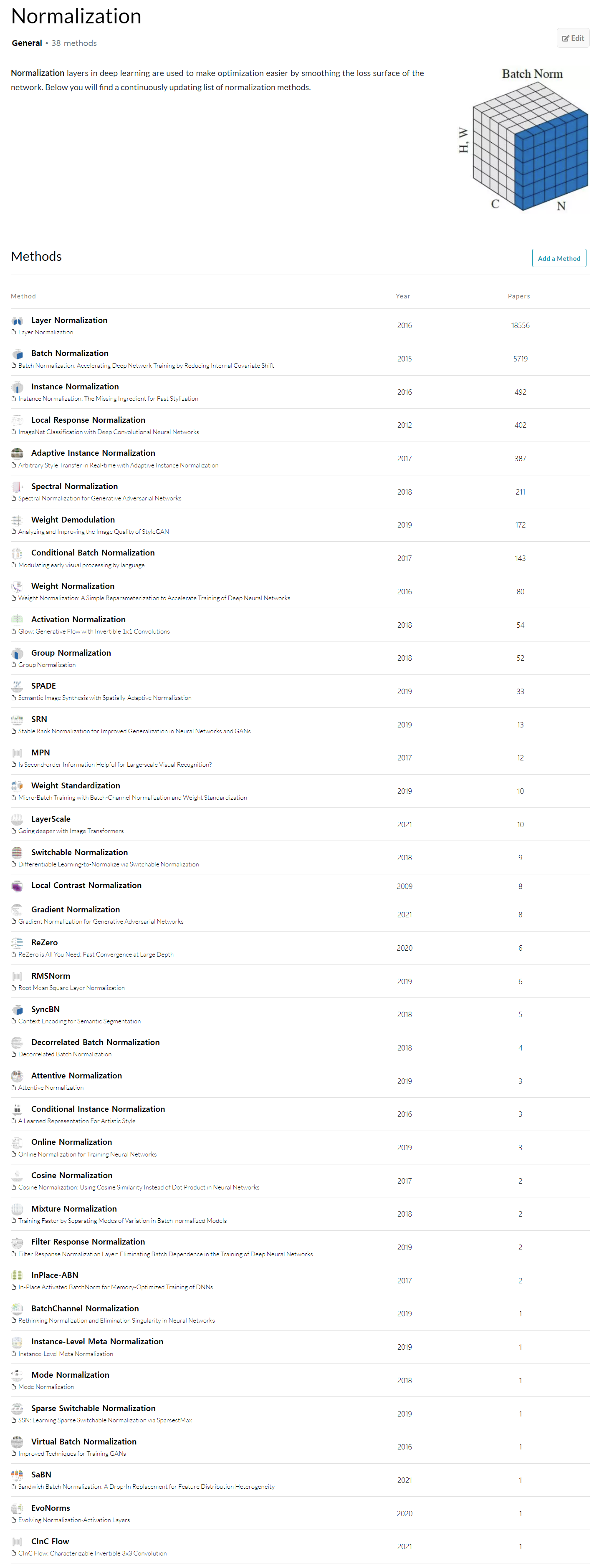
2. PaperswithCode 활용

methods 별로 나온 연도, 논문 수에 따라 나열해 주고 각 방법에 대한 설명 및 요약, 수식, 코드, 논문까지 한번에 확인 가능

논문 | 코드 | 설명을 한번에 GPT에 넣어서 설명 및 예시 코드에 대해 확인 가능

학습 소감

  • 선형 대수 | 자료구조 | 통계 | 컴퓨터과학이 결합되 탄생한 딥러닝인 만큼 이에 대한 피상적인 이해가 아닌 깊은 이해를 위해서는 추가적인 공부 및 논문 리뷰가 필요할 것으로 생각됨

→ 강의와 함께 관련 서적을 구매하여 공부하고 있음

  • Line by Line으로 실습용 노트북 파일이나 캐글 노트북 등을 따라 쓰면서 torch에 대해 더 익숙해져야할 필요가 있다고 느낌

ps.
애플실리콘 전용 Array Framework

MLX 쓰는게 numpy나 pytorch로 짜는것보다 더 빠릅니다. 근데 API가 거의 비슷해서 배우는데 어렵지 않습니다 :)

profile
Sylen
AI가 재밌는 걸
이전 포스트

[Upstage AI Lab 3기] ML 프로젝트 기본 이론 : 머신러닝

다음 포스트

[Upstage AI Lab 3기] 과정 중반 회고

0개의 댓글