고전 컴퓨터 비전의 Filter

Sobel Filter : 정해진 Sobel Kernel을 통해 x 방향과 y방향으로 변화율을 계산하여 엣지를 검출하게 되며, 학습 가능하지 않음

CNN의 Filter : 학습가능

Convolution Filter

- Convolution 연산을 통해 산출한 결과를 정답지 (Ground Truth, GT)와 비교하여 오차를 줄여나가는 방식 등으로 계속 업데이트 되는 학습 가능한 필터를 많이 사용하게 됨

- 고전 컴퓨터 비전의 방법만으로는 성능이 좋지 않거나 해결이 불가능했던 태스크들을 할 수 있게 됨

학습가능한 파라미터란?

학습가능한 파라미터들을 가진 레이어의 예시

Convolution Layer

Parameters = $(F_{in} * F_{in} * C_{in} + 1 ) * C_{out}$

• 네트워크가 비전 태스크를 수행하는 데에 유용한 Feature들을 학습할 수 있도록 함
• Convolution Layer를 여러개 쌓는 경우, 뒤 레이어의 결과값 하나를 만드는데 사용되는 이미지의 범위가 넓어진다.
• 뒷레이어로 갈 수록 Receptive field
• Convolution Layer의 초반 Layer의 경우 Edge와 같은 low-level feature를 주로 학습하게 되고, 후반 Layer의 경우 shape과 같은 high-level feature를 주로 학습하게 됨

Batch Normalization Layer

Parameters = 2 * $C_{in}$...($\gamma,\beta$)

www

• zero mean normalization을 다시 scaling shift 할때 사용되는 감마wddddddd은 실제로 정답지와 오차를 학습하여 계산된 파라미터wwwwww
• 즉 batch Normalization의 패러미터는 2 * $C_{in}$
• Batch Normalization에서 각 배치의 이동평균으로 계산한 평균과 분산을 저장하고 있지만, 이는 테스트 데이터에 대한 Inference를 위함

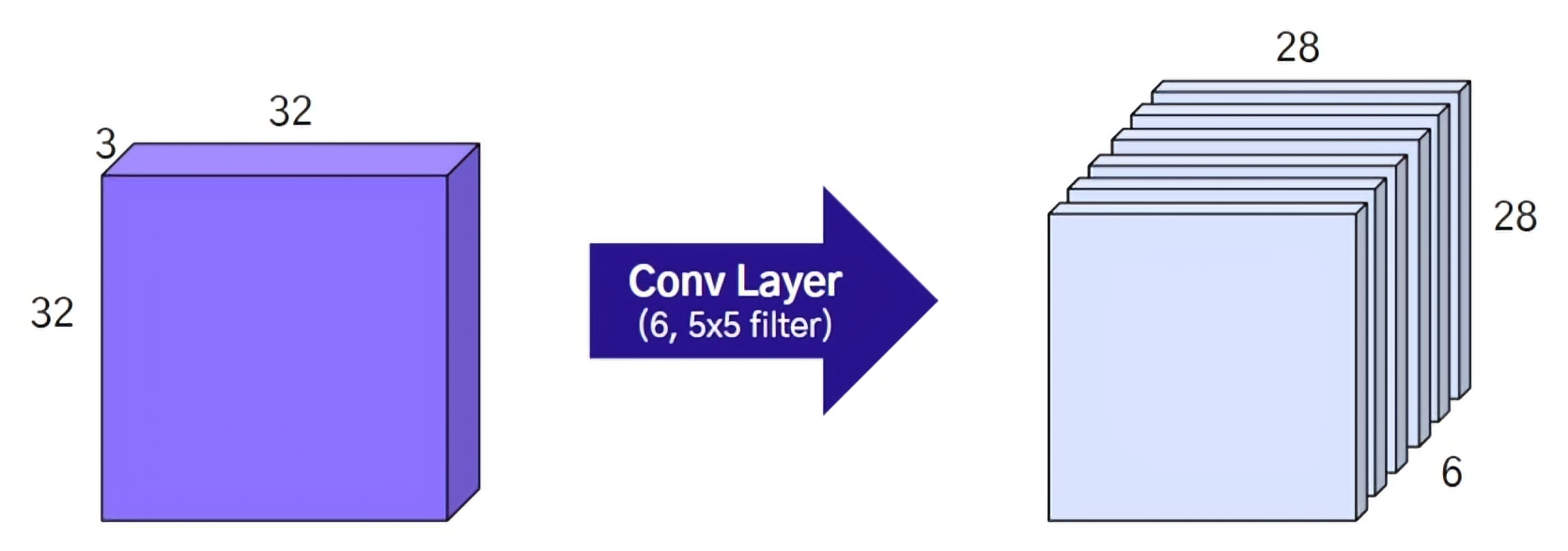
6개의 Feature Map을 얻을 수 있다.

• DeepNetwork가 잘 학습될 수 있도록 함
• Gradient Flow를 개선시킴
• 더 빠르게 Converge될 수 있도록 함
• 학습 시 regularization을 한 것 같은 효과를 얻을 수 있음
• 좀 더 robust한 모델이 될 수 있도록 하는 데 기여함 (즉, Overfitting을 방지하는 데에 도움을 줌)
• 보통 Convolution Layer 다음, 그리고 Activation Layer전에 Batch Normalization을 해줌

=> 작은 Weight 변화에 Sensitive하지 않아 Optimize 하기 쉬워쥠

Fully Connected Layer

Parameters = $(N_{in} * N_{in} * C_{in} + 1) * M$

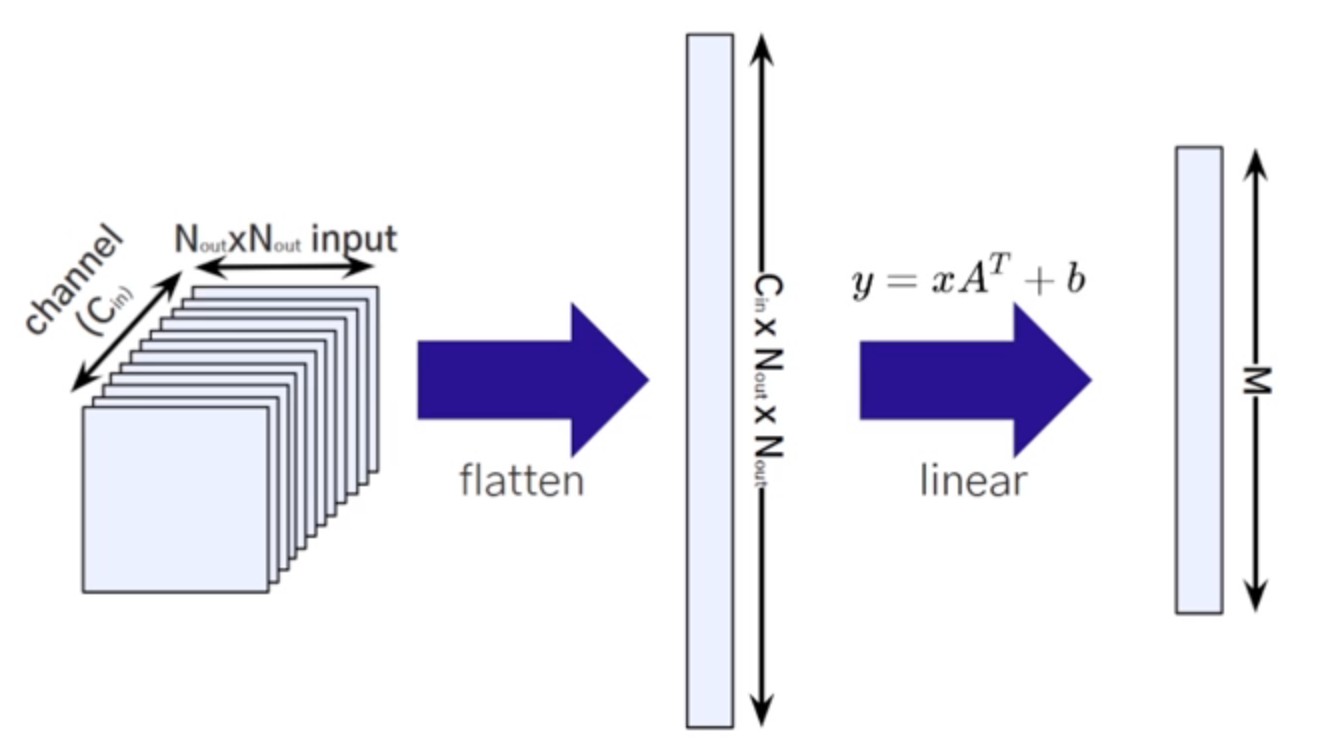
Flatten 후 Linear 연산을 하게 됨

학습 불가능한 레이어의 예시

Activation Layer

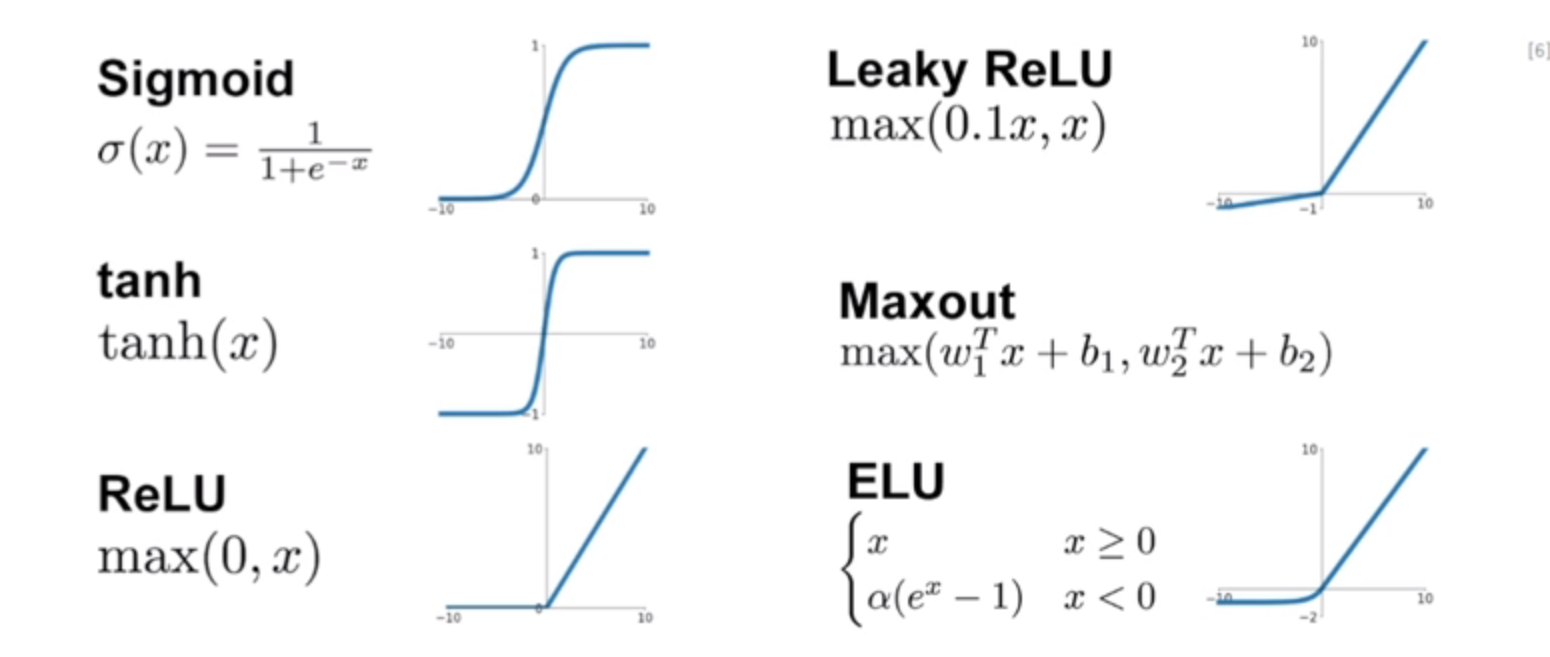
• 모델에 비선형성을 부여해주기 위해서 사용됨
• 선형함수의 Layer들로만 구성될 경우 여러개를 쌓더라도 선형함수 하나로 표현될 수 있는 모델이 될 뿐이기 때문에, 깊은 네트워크의 장점을 살릴 수 없게 됨
  

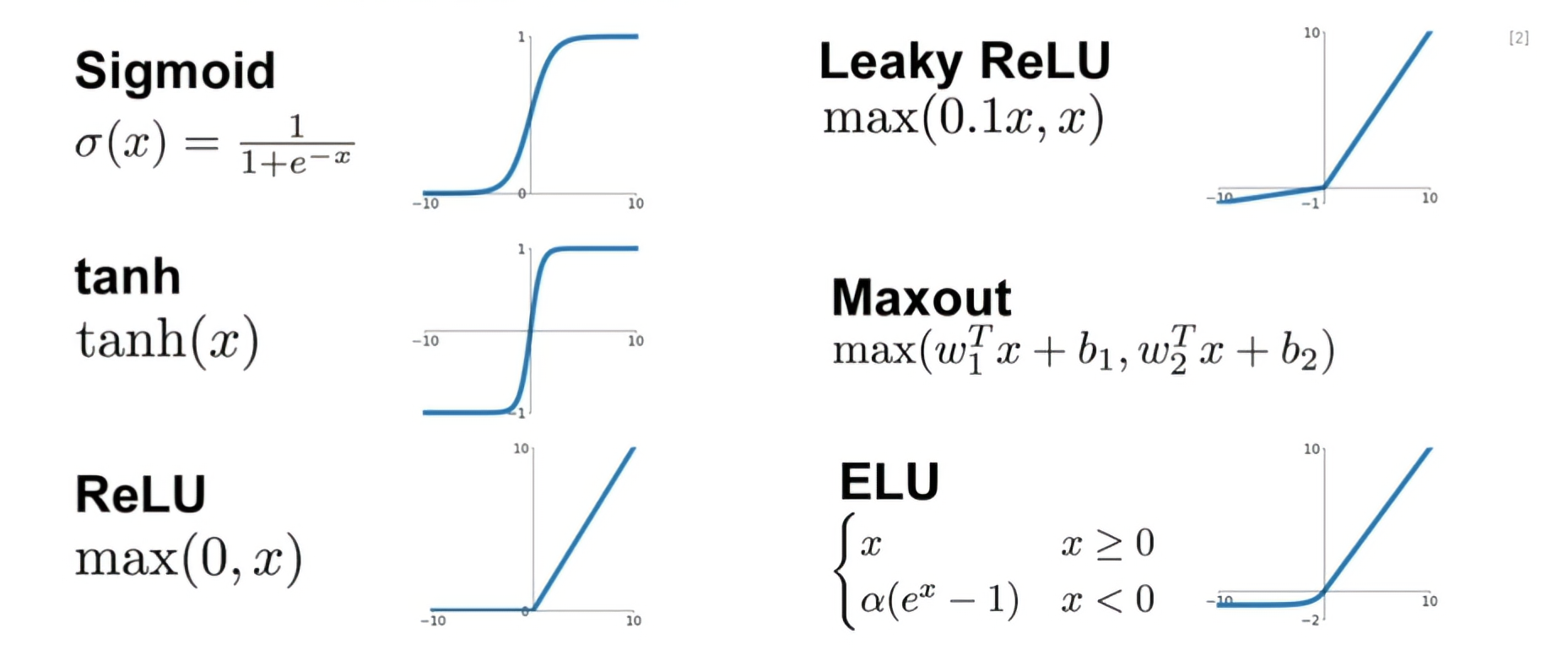
Sigmoid

• 입력값에 상관없이 출력값이 항상 0과 1사이
• Gradient 값이 kill 되는 현상이 생길 수 있음
• Sigmoid를 거친 결과는 0에 Centroid 되어 있지 않음 (중간값이 0.5라는 애매한 값)
• Exponential 함수를 계산해야 하므로 Cost가 높음

tanh

• 여전히 gradient 값이 kill 되는 현상이 생길 수 있음
• tanh를 거친 결과는 0에 centroid 되어 있음

ReLU

• 양수의 값을 가질 경우 gradient가 kill되지 않음
• Computational cost가 매우 작음
• Sigmoid나 tanh함수보다 매우 빠르게 수렴함
• ReLU를 거친 결과는 Zero-Centroid가 아님
• 음수값을 가질 경우 Gradient가 0이므로 update 되지 않음

Leaky ReLU : $max(0.1x,x)$ (음수값이 0이 아니게 보완)

Pooling Layer

• Feature Map에 Spatial Aggregation을 모델의 파라미터 수를 줄여줌
• 더 넓은 Receptive Field를 볼 수 있게 해줌

Max Pooling : Filter를 거친 뒤 가장 큰 값만 가져감

• 정보 손실이 일어날 수 있음
  

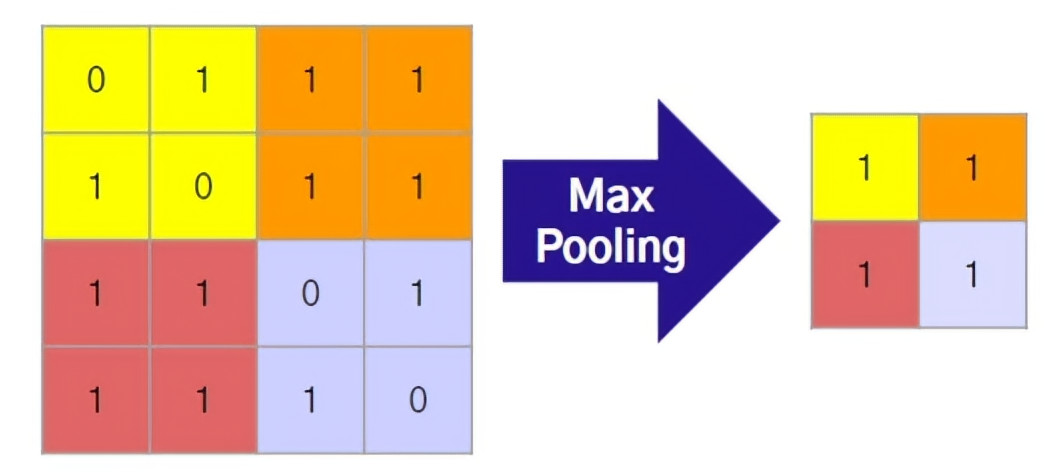
Average Pooling : Filter를 거친 평균값을 가져감

• 중요한 정보가 희석될 수 있음