[게임 수학] #9 아핀 공간(2)

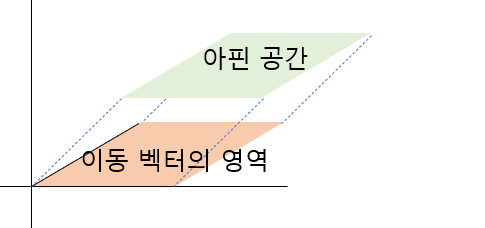
아핀 공간의 구성요소

점

아핀 공간에서의 점은 마지막 차원값이 1인 아핀 공간의 원소로 나타난다.
예를 들면 2차원 공간에서의 점은 항상 $(x, y, 1)$의 형태로 표현된다.
3차원 공간에서의 점은 $(x, y, z, 1)$로 표현되고, 여기서 (x, y, z)는 점의 실제 좌표값이며 마지막 값 1은 아핀 공간에서 점을 표현하는 데 사용된다.

이동 벡터

아핀 공간은 벡터 공간의 부분벡터이다. 아핀 공간에서 이동 벡터는 한 점에서 다른 점으로 이동하기 위한 방향과 거리를 나타낸다. 기존에 알던 벡터와 이름도 개념도 유사하지만 다른 용도로 사용되므로, 둘을 구분하기 위하여 아핀 공간의 벡터를 이동 벡터 혹은 변위 벡터라고 칭한다.

두 점 사이의 상대적인 위치 변경을 나타내고자 이동 벡터는 두 점을 연결하는 화살표로 표현되는데, 이는 두 점 사이의 최단거리와 같다.

아핀 공간의 특정한 하나의 점 $P_1$에 이동벡터 $\overrightarrow{v}$를 더한 결과는 또 다른 아핀 공간의 특정한 하나의 점 $P_2$이다. 이를 식으로 나타내면 다음과 같다.
$P_1+\overrightarrow{v}=P_2$
여기서,
$\overrightarrow{v} = P_2-P_1$를 도출할 수 있다.

아핀 공간의 두 점을 각각 $P_1(x_1,y_1,1), P_2(x_2,y_2,1)$라고 가정하면 이동벡터$\overrightarrow{v}$는 $(x_1-x_2,y_1-y_2,0)$의 형태를 띈다.

아핀 결합