[게임 수학] #8 아핀 공간(1)

아핀 공간

행렬을 이용한 벡터의 이동은 덧셈으로 구현할 수 있다.
$\begin{bmatrix}x\\y\\ \end{bmatrix}+\begin{bmatrix}a\\b\\ \end{bmatrix}=\begin{bmatrix}x+a\\y+b\\ \end{bmatrix}$

하지만 행렬 곱은 선형 변환만을 표현할 수 있으므로 이와 같은 이동을 만들어낼 수 없다.

$A*\begin{bmatrix}x\\y\\ \end{bmatrix}=??\begin{bmatrix}x+a\\y+b\\ \end{bmatrix}$

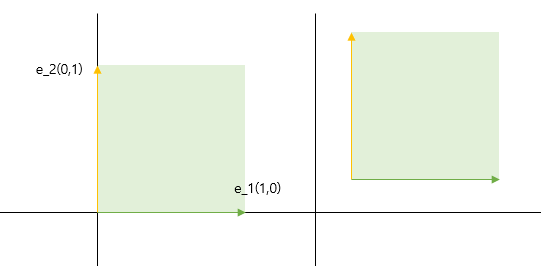
선형성을 만족하기 위해서 기저벡터는 항상 원점에서 출발해야하지만 벡터를 이동시킬 때 기저벡터가 움직이는 것을 피할 수 없다.

행렬의 곱으로 이동 기능을 구현하는 방법이 존재하는데, 이 방법은 벡터 공간의 일부에만 적용할 수 있다. 이 방법을 적용하여 이동이 가능한 부분공간을 바로 아핀 공간이라고 한다. 아핀 공간은 결과적으로 이동 변환을 위한 개념으로, 이동 변환은 벡터 공간에서의 연산으로는 표현하기 어려운 이동을 나타낼 수 있게 해준다.

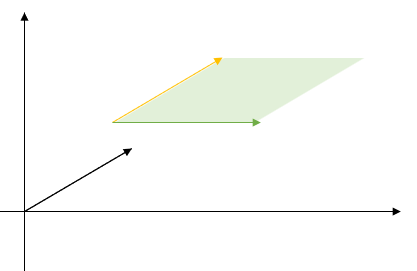
2차원 벡터를 표현하기 위한 두 개의 차원에 하나의 차원을 더 추가하면 선형 변환의 형태로 이동을 구현할 수 있다.

이전에 학습한 전단 변환은 표준 기저벡터 $e_1$를 고정시킨 상태로 옆으로 밀어서 공간을 평행사변형 꼴로 기울인다. 위의 그림은 전단변환을 이용해 x축 방향으로 각각 0, 1, 2 만큼 민 공간이다.

초기 공간에서는 y가 1인 영역의 x값은 [0,1]의 범위를 갖는다. x축으로 1만큼, 2만큼 민 공간에서의 x값은 [1,2]와 [2,3]으로 변하는데, 이는 전단 변환을 사용해 공간을 오른쪽으로 민다면 y값이 1인 영역의 x범위는 밀어낸 만큼 그대로 이동하게 된다.

벡터의 y값을 1로 고정하고 전단변환을 적용하면 다음 식이 나온다.

$\begin{bmatrix}1&a\\0&1\\ \end{bmatrix}*\begin{bmatrix}x\\1\\ \end{bmatrix} = \begin{bmatrix}x+a\\1\\ \end{bmatrix}$

이 식은 1차원의 이동 변환과 같다. 그러므로 2차원의 이동 변환을 구현하려면 3차원 공간으로의 확장이 필요한 것이다.

$\begin{bmatrix}1&0&a\\0&1&b\\0&0&1\\ \end{bmatrix}*\begin{bmatrix}x\\y\\1\\ \end{bmatrix} = \begin{bmatrix}x+a\\y+b\\1\\ \end{bmatrix}$

여기서, $\begin{bmatrix}1&0&a\\0&1&b\\0&0&1\\ \end{bmatrix}$는 $T$로, 이동 변환행렬이라고 한다. 이동 변환행렬에서 이동에 사용될 벡터는 항상 마지막 차원값이 1이어야 한다. 이 추가된 마지막 차원 값이 1이라는 조건을 만족하는 부분 공간이 바로 아핀 공간이다.

이전에 학습한 크기 변환행렬과 회전 변환행렬은 2x2 크기였다.

크기 변환행렬 : $\begin{bmatrix}a&0\\0&b\\ \end{bmatrix}$
$\theta$ 회전 변환행렬 : $\begin{bmatrix}cos\theta&-sin\theta\\sin\theta&cos\theta\\ \end{bmatrix}$

이동 변환에 맞게 3차원으로 위 행렬들을 늘리면 다음과 같은 3x3 정방행렬이 된다.
크기 변환행렬 $S$ : $\begin{bmatrix}a&0&b\\0&b&0\\0&0&1\\ \end{bmatrix}$
$\theta$ 회전 변환행렬 $R$ : $\begin{bmatrix}cos\theta&-sin\theta&0\\sin\theta&cos\theta&0\\0&0&1\\ \end{bmatrix}$

$S, R, T$는 하나의 차원을 추가하여 만들어낸 아핀 변환이다.