Deep Unsupervised Learning using Nonequilibrium Thermodynamics
Abstract
논문에서는 non-equilibrium statistical physics에 영감을 받아 forward diffusion process 과정에서 데이터 분포의 구조를 체계적이고 천천히 파괴하고, 데이터의 구조를 복원하는 reverse diffusion process를 통해 flexibility와 tractability 성질을 가지는 생성 모델을 만들 수 있는 방법을 제시한다.
Introduction
기존 확률 모델의 경우 tractability와 flexibility 사이에서 trade-off가 발생한다. 예를 들어서, tractable model 같은 경우는 제한된 데이터 셋에 대해서만 학습되는 경향이 발생하고 flexible model의 경우는 정규화 상수에 대한 계산이 필요한데 이는 일반적으로 다루기 힘들고 계산 비용이 많이 소요되는 Monte Carlo process가 필요하다.
Diffusion probabilistic models
제안하는 probabilistic model은 다음을 가능하게 하는 특징을 가진다.
- 모델 구조의 flexibility
- 정확한 표본 추출
- 다른 분포와의 쉬운 곱셈 (e.g. 사후 계산)
- model log likelihood와 각 state에 대한 쉬운 확률 계산
제안하는 알고리즘은 non-equilibrium statistical physics와 sequential Monte Carlo에 사용된 Markov chain을 사용하여 하나의 분포에서 다른 분포로 점진적으로 변환하는데, 구체적으로 잘 알려진 분포(e.g. 가우시안 분포)를 목표 분포로 변환하도록 Markov chain을 구축
diffusion chain의 각 단계는 계산가능한 확률을 가지므로 전체에 대한 확률 계산 또한 가능하다.
학습 프레임워크에는 diffusion process에서 작은 변화를 추정하는 것이 포함되는데, 이는 정규화할 수 없는 잠재적인 함수로 전체 분포를 명시적으로 설명하는것보다 tractable하기 때문이다.
Markov Property : 과거 상태들에 대해 독립적이고, 오직 현재 상태만이 다음 상태로의 변환에 영향을 미친다.
Relationship to other work
웨이크-슬립 알고리즘(1995)은 추론과 생성 확률 모델 서로에 대해 학습시키는 아이디어를 도입했다. 이후 20년동안 발전되지 않다가 최근 이 아이디어를 발전시키는 연구가 증가하고 있는데, 주로 잠재 변수에 대해 유연한 생성 모델과 사후 분포를 서로 직접 훈련할 수 있는 변형 학습 및 추론 알고리즘이 개발되었다.
이 연구들과 논문에서 제안하는 방법의 차이점은 크게 다음과 같다.
- 가변 베이지안 방법이 아닌 physics, quasi-static processes, annealed importance sampling 아이디어를 사용
- 학습된 분포를 다른 확률 분포와 곱하기 쉬운 특성 (e.g. 사후 계산을 위해 조건부 분포와 함께)
- reverse diffusion process가 동일한 함수 형태를 가지도록 forward diffusion process를 단순한 함수 형태로 제한하여 추론 모델 학습 어려움에 대한 문제 해결
- 몇 개의 레이어가 아닌 수천 개의 레이어의 모델 학습
- 각 단계에서 엔트로피 생성에 대한 상한과 하한을 제공
Algorithm
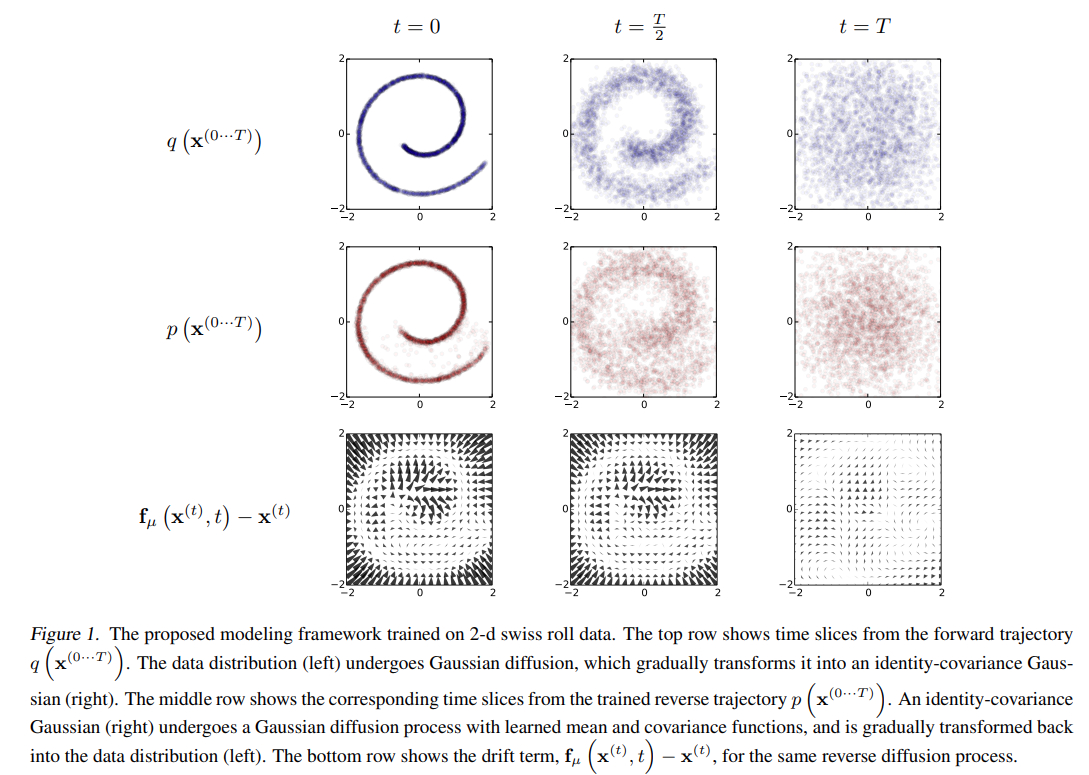
논문에서는 복잡한 데이터 분포를 단순하고 다루기 쉬운 분포로 변환하는 forward diffusion process를 정의하고 diffusion process의 finite-time reversal을 학습하는 것을 목표로 하고 있다.
Figure 1는 reverse diffuion process에서 어떻게 학습되고 확률을 평가하는데 사용할 수 있는지 보여준다.
논문에서는 먼저 inference diffusion process인 forward 과정을 보여주고, reverse process에 대한 엔트로피 경계를 유도하고 학습된 분포가 어떻게 임의의 두 번째 분포에 곱해질 수 있는지 보여준다. (e.g. 이미지를 채색하거나 노이즈를 제거할 때 사후를 계산하기위해 수행하는 것)
Forward Trajectory
데이터 분포 는 Markov diffusion kernel 를 반복적으로 적용하여 목표 분포 로 변환된다. 여기서 는 diffusion rate 의미. 이 과정은 다음과 같다.
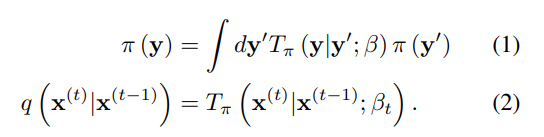
데이터 분포 에서 단계로 diffusion 진행하는 것을 표현하면 다음과 같다.
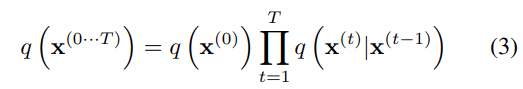
여기서, 는 동일한 공분산을 갖는 가우시안 분포로의 가우시안 확산 혹은 독립적인 이항 분포로의 이항 확산을 의미한다.
Reverse Trajectory
생성 분포는 동일한 trajectory을 가지도록 학습되지만, 반대의 과정으로 진행된다.
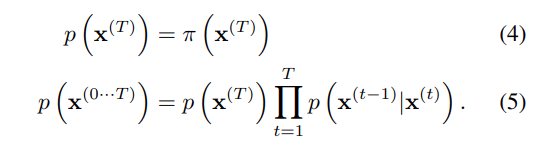
가우시안과 이항 확산 모두 연속 확산에 대해 확산 과정의 반전은 forward process와 동일한 함수 형태를 갖는다. 의 값이 작다면, 이 가우시안(이항) 분포기 때문에 반대의 경우 또한 가우시안(이항) 분포를 가진다. trajectoy가 길어질수록 diffusion rate 가 작아질 수 있다.
학습이 진행되는 동안 가우시안 확산 커널에 대한 평균과 공분산 또는 이항 커널에 대한 비트 플립 확률만 추정만 수행되어야 한다.
이 알고리즘의 계산 비용은 이러한 함수의 비용과 time step의 수를 곱한 값이 되고, MLP를 통해 이 기능을 정의한다.
Model Probability
데이터 분포에 대한 생성 모델의 확률은 다음과 같다.
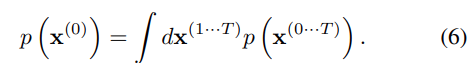
이 적분을 annealed importance sampling와 Jarzynski equality를 응용해서 평균화한 forward trajectory와 reverse trajectory의 상대 확률을 평가한다.

Training
학습은 log likelihood를 최대화하는 방향으로 진행된다.
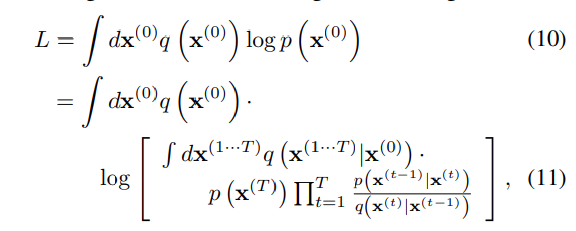
Jenson 부등식에 의해 은 lower bound를 가진다.

Appendx에 의해 는 다음과 같이 KL divergence와 엔트로피들로 표현할 수 있다.
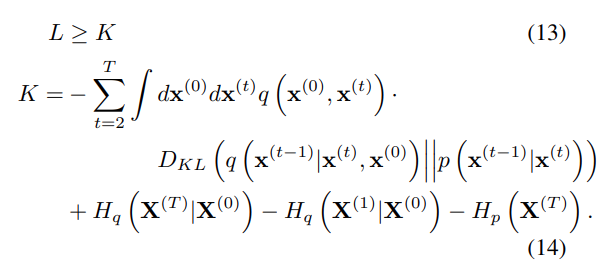
여기서, forward와 reverse trajectories가 동일하다면 식 13에서 과 는 동일한 값을 갖는다.
학습은 log likelihood에서 lower bound를 최대화하는 reverse Markov transition를 찾는 과정으로 구성된다.
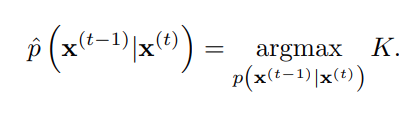
Setting The Diffusion Rate
forward trajectory에서의 값은 모델의 성능에 중요한 영향을 미친다.
Gaussian Diffusion의 경우, 는 에 대한 gradient ascent로 구했고, 는 overfitting을 막기 위해 고정된 작은 값을 사용했다. binomial diffusion의 경우, frozen noise를 포함한 gradient ascent가 불가능하므로, 를 사용
Multiplying Distributions, and Computing Posteriors
Denosing이나 inpainting을 위해서는 모델 분포 에 bounded positive function 을 곱해야 한다.
Multiplying distribution은 기존 다른 모델(e.g. autoencoder, GSNs, NADEs etc..)에 대해서 어렵지만, diffusion 모델의 경우는 각 step에서의 small pertubation으로 취급하거나 다른 step에 대해서 정확하게 곱해지는게 가능하다.

Modified Marginal Distributions
수정된 reverse trajectory를 를 의미하고 중간 분포의 시퀀스를 통해 진행되는 과정을 다음과 같이 표현할 수 있다.
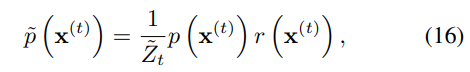
여기서, 는 t-th 중간 분포를 위한 정규화 상수를 의미한다.
Modified Diffusion Steps
reverse diffusion 과정에 대한 Markov kernel 은 평형 조건을 준수한다.

perturbed Markov kernel 또한 위의 조건을 따른다고 가정하면 다음과 같이 유도할 수 있다.
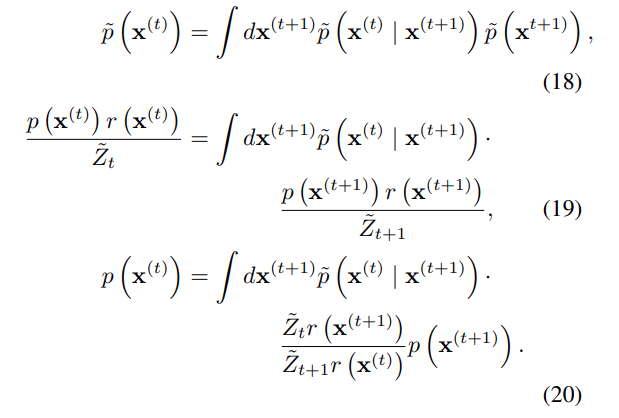
식 20을 정리하면 다음과 같다.
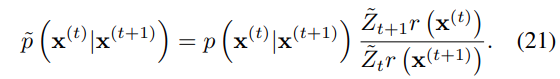
식 21의 경우, 정규화된 확률 분포를 따르지 않을 수 있으므로 이 정규 분포에 대응되도록 수정하면 다음과 같다.
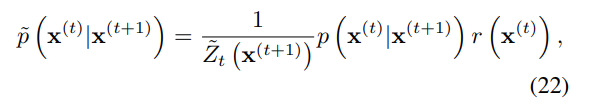
여기서, 은 정규 상수가 된다.
Applying
가 충분히 부드럽다면 이는 reverse diffusion kernel 에 대한 작은 pertubation으로 생각할 수 있고, 이 때 는 와 같은 형태를 띄게 된다. 만약, 가 가우시안 분포와 closed form으로 곱할 수 있다면 는 에 closed form으로 곱할 수 있게 된다.
Choosing
는 trajectory에 따라 천천히 변하는 함수이어야 하며, 실험에서는 상수로 적용했다.
Entropy of Reverse Process
Forward Process를 알고 있기 때문에 Reverse Process에서 각 step의 조건부 엔트로피에 대한 upper & lower bound를 구할 수 있으므로 이를 log likelihood에 대해서 표현하면 다음과 같다.
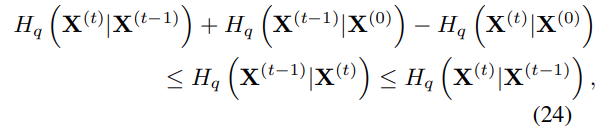
upeer & lower bound는 에만 의존하므로 계산할 수 있다.
Experiments
-
Dataset: Toy data, MNIST, CIFAR10, Dead Leaf Images, Bark Texture Images
-
각 데이터셋에 대한 생성 및 impainting
forward & reverse diffusion kernel은 각각 다음과 같다.
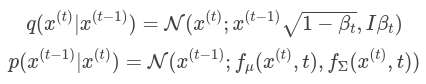
여기서, , 은 mlp를 의미하고 또한 학습 가능한 파라미터이다.

Conclusion
논문에서는 확률에 대한 정확한 샘플링 및 평가를 가능하게 한 확률 분포 모델링을 위한 새로운 알고리즘을 제안했다.
제안한 알고리즘을 통해 다양한 데이터 셋에 대해서 효과를 입증했으며 이를 통해 다양한 분포를 정확하게 모델링할 수 있음을 보여준다.
제안하는 알고리즘의 핵심은 데이터를 노이즈 분포에 매핑하는 Marcov Diffusion Chain의 Reverse를 추정하는 것이며 이를 통해 어떠한 데이터 분포에도 적합성을 학습할 수 있으면서도 조건 및 사후 분포를 쉽게 컨트롤할 수 있는 장점이 있다.

좋은 글이네요. 공유해주셔서 감사합니다.