0. 학습목표
- 상황에 맞는 귀무가설과 대립가설을 세울 수 있다.
- 1종 오류와 2종 오류를 설명할 수 있다.
- 유의 수준을 이용하여 옳은 가설을 채택할 수 있다.
1. 주요개념
1-1 가설 검정
관심 있는 특정 모집단의 특성에 대한 가설을 세우고, 이 가설을 샘플 데이터를 사용하여 검토하는 추론의 과정을 말한다.
1-1-1. 귀무가설(Null Hypothesis)
default가설로 특별한 사유가 없다면 받아들여지는 가설을 의미한다. 내가 검증하고 싶은 주장의 영가설이며, 어떤 대상을 비교하는 경우 비교 대상간에 아무런 차이가 없다는 의미를 담고 있다.
1-1-2. 대립가설(Alternative Hypothesis)
귀무가설이 충분한 증거로 기각되었을 때 채택되는 가설이다. 귀무가설과 대립되며, 우리가 사실이라고 증명하고자 하는 사실을 의미한다. 수학적으로 등호를 포함하지 않는다.
1-1-3. 검정 통계량(Test Statistics)
샘플 데이터에서의 통계량을 의미한다.
1-1-4. 유의 확률(p-value)
귀무가설을 지지하는 정도를 나타내며, 귀무가설이 맞다고 가정할 때 얻은 결과보다 극단적인 결과가 실제로 관측될 확률을 의미한다.
즉 p-value = 0.05라면 이 경우는 5%의 확률로 결과보다 극단적인 결과가 관측된다는 말이다. 따라서 p-value가 유의수준보다 낮아져 0에 가까울수록 귀무가설은 기각된다. 0.0001%의 확률로 우연하게 결과가 도출되었다고 생각하는 것보다, 어떤 차이가 존재하는 것으로 인식해야하기 때문이다.
1-1-5. 표본분포(Sampling Distribution)
모집단에서 샘플을 복원추출하고, 매 추출마다 통계치를 계산하였을 때 그 표본의 통계치로 그린 분포를 의미한다.
1-1-6. 양측검정
크거나 작은 경우 모두를 고려하여 검정하는 방식이다. 정규분포는 평균을 중심으로 대칭이기 때문에 유의 수준을 반으로 나누어 양측에 사용한다.
1-1-7. 단측검정
어떤 가정보다 크거나 또는 작을 경우를 검정하는 것을 의미한다. 작은 것을 검정할 경우 좌측 검정리하며, 큰 것을 검정할 경우 우측 검정이라고 한다.
2. 오류
2-1. 1종오류(False Positive)
귀무가설이 참인데 기각한 경우로, 예로는 남자는 죄가 없는데 죄가 있다고 잘못 판단한 경우이다. 이는 alpha로도 지칭하며 유의수준 이라고도 한다. 유의수준이란 귀무가설이 참인데도 불구하고 기각할 확률을 의미하며 이 값이 0.05보다 작으면 귀무 가설을 잘못 기각할 가능성이 5%미만이며, 그만큼 잘못 기각할 가능성이 낮음을 인정하고 우리는 귀무가설을 기각할 충분한 증거를 확보했다는 의미하다.
2-2. 2종오류(False negative)
귀무가설이 거짓인데 기각하지 않은 경우로, 위의 예로는 남자는 죄가 있는데 죄가 없다고 잘못 판단한 경우이다. 이는 Beta로 지칭된다.
3. 검정 방법론
3-1. 신뢰구간 확인
가지고 있는 샘플 데이터로 평균의 표본 분포(sampling distribution of mean values)를 시뮬레이트 한 뒤, 이를 모집단의 분포라고 가정한다. 그리고 이 분포에서 95%신뢰구간을 확인한 뒤, 귀무가설이 이 표본 분포 어디에 해당하는지 확인하여 귀무가설을 채택할지 기각할지를 결정한다.
3-2. p-value확인
p-value란, 귀무가설이 맞다는 전제 하에, 통계값이 실제로 관측된 값(샘플의 통계치) 이상일 확률을 의미한다. 귀무가설이 사실임을 가정하고, 귀무가설이 대립가설과 가장 근접하게 있는 값으로 귀무 분포를 시뮬레이트 한 뒤, 샘플 데이터에서 평균값이 이 분포 어디에 존재하는지를 확인한다. 그리고 이 평균값보다 큰 부분을 확인함으로서 어떤 가설을 채택할지 결정한다.
2. 추가개념
2-1. T-test(t 검정)
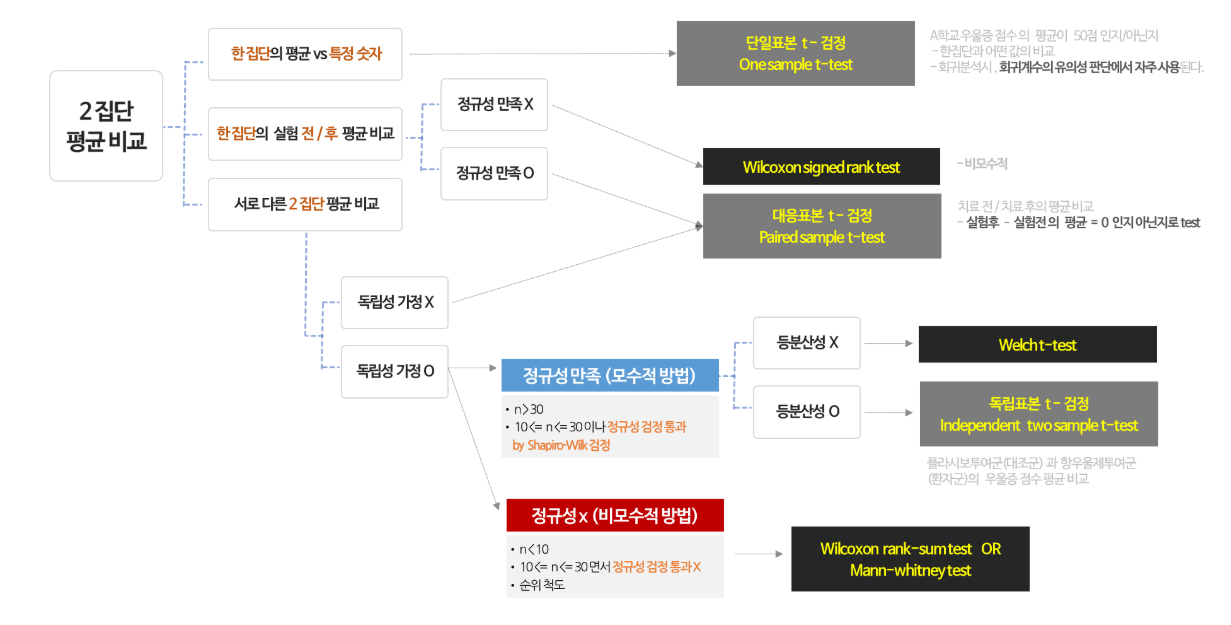
t 검정이란 모집단의 분산이나 표준편차를 알지 못할 때 모집단을 대표하는 표본으로부터 추정된 분산이나 표준편차를 가지고 검정하는 방법을 의미한다.
"두 모집단의 평균 간의 차이는 없다."라는 귀무가설과 "두 모집단의 평균 간에 차이가 있다."라는 대립 가설 중에 하나를 선택할 수 있도록 하는 통계적 검정 방법이다.
3. 명령어
3-1. scipy.stats.ttest_1samp()
하나의 점수 그룹의 평균에 대한 T-검정을 계산한다. 독립 관측치인 a 표본의 평균이 주어진 모집단 평균과 같다는 귀무가설에 대한 검정이다.
scipy.stats.ttest_1samp( a, popmean, axis, nan_policy, Alternative)a: 관찰 샘플의 배열을 의미한다.
popmean: 귀무가설에 사용되는 기준 값을 의미한다.
나머지는 그때 그때 찾아보자.
❗ 참고사이트:
official scipy.stats.ttest_1samp
3-2. scipy.stats.ttest_ind()
두 개의 독립적인 표본의 평균에 대한 T-검정을 계산한다. 이 명령어는 2개의 표본이 동일한 평균값을 갖는다는 귀무가설에 대한 검정이다. 이 검정을 시행하기 위해서는 다음과 같은 가정이 필요하다.
- 한 표본의 관측치는 다른 표본의 관측지와 독립적이여야 한다.
- 데이터는 대략적으로 정규 분포를 따라야한다.
- 두 표본의 분산은 거의 같아야 한다.
- 두 샘플의 데이터는 무작위 샘플링 방법을 사용하여 얻어야 한다.
scipy.stats.ttest_ind(a,b,axis=0,equal_var=True,
nan_policy='propagate',permutations=None, random_state=None,
aleternative='two-sided',trim=0)a,b: 비교하고자 하는 두 표본이다.
equal_var: 등분산 가정이다.
alternative: 검증 방식을 선정한다. greater는 우측검정,less는 좌측검정,two-sides는 양측검정을 의미한다.
이 이상은...
❗ 참고사이트:
official scipy.stats.ttest_ind
4. 회고
사실 검정부분에 대해서는 실험통계학에서 다루어서 크게 오늘 내용이 어렵지는 않았다. 단지 확통이 나한테 너무 안맞을뿐...차라리 미분방정식 푸는게 더 맛있을 거 같다. 내가 미분방정식을 찾는 날이 올 줄이야...
