0. 학습목표

• Scalar, Vector, Matrix에 대해서 이해한다.
• Span, Basis, Rank에 대해서 이해한다.
• Numpy를 사용하여 선형대수 연산을 할 수 있다.

1. 주요개념

먼저, 이번 sprint에서는 선형대수를 주로 다룬다. 이번 1차시에는 기본적인 행렬과 벡터에 대해서 학습하였다. 그에 대한 기본 연산 수행 방법을 학습하였지만, 행렬의 연산에 대해서는 상세히 다루지 않겠다.

1. Span

벡터공간 $V$에 대하여 집합 $S$를 $S = \{ v_i |v_i \in V , i \in I \}$라 하자. 이 때 span은 다음과 같이 정의된다.

$span(S)$ : $S$에 속하는 벡터들의 선형 결합으로 나타날 수 있는 모든 벡터의 집합. 이 때 $span(S)$는 $V$의 $subspace$로서 벡터공간이 된다.
ex)
$span(\{ \left[ \begin{matrix} 0 \\ 1 \\ \end{matrix} \right] , \left[ \begin{matrix} 1 \\ 1 \\ \end{matrix} \right] \}) = \R^2$
$span(\{ \left[ \begin{matrix} 0 \\ 1 \\ \end{matrix} \right] \}) = \{(0, y)| y \in \R \}$

$span(S) = V$일 때, $S$의 원소의 갯수는 $V$에 속하는 선형 독립적인 벡터들의 집합의 원소의 갯수보다 같거나 크다.

2. Basis

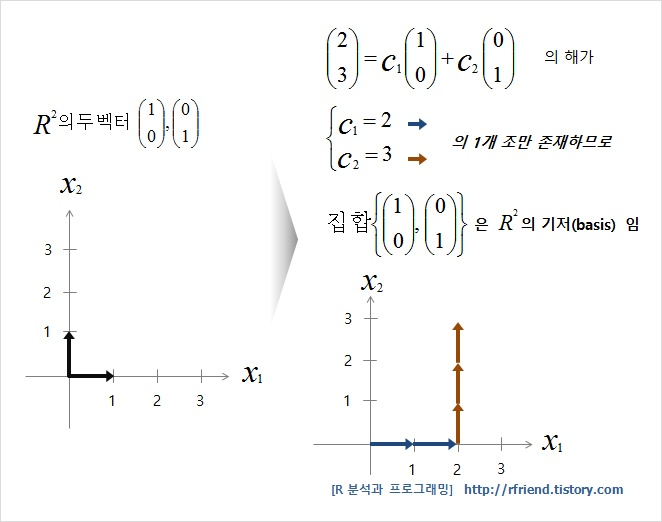
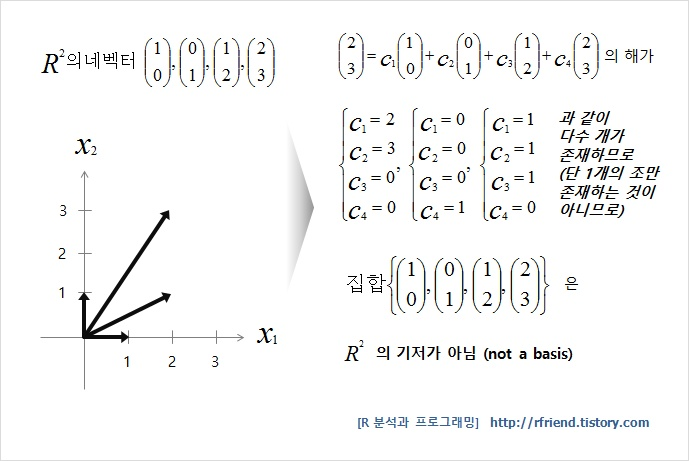
기저란 어떤 벡터공간 V의 벡터들이 선형독립이면서 벡터공간 V 전체를 생성할 수 있다면 이 벡터들의 집합을 말한다. 즉, 기저는 $R^m$의 임의의 원소를 표현하기 위해 필요한 최소한의 벡터로 이루어진 집합이다.

“벡터공간 V에 속한 1차 독립인 벡터들의 최대집합을 벡터공간 V의 기저(basis)라고 한다.”

3. Rank

행렬 $A$에 대해서 rank는 다음과 같이 정의된다.

• $rank(A)$ : $A$의 열공간에 대한 차원. 즉 $A$의 열벡터들을 선형 결합하여 나오는 벡터공간($C(A)$)에서 선형 독립인 벡터의 최대 갯수를 의미한다. column rank와 같은 의미이다.

ex)
ex) $A = \left[ \begin{matrix} 1 & 2 \\ 3 & 4 \\ \end{matrix} \right]$ 인 경우 $rank(A) = 2$ , $A = \left[ \begin{matrix} 1 & 2 & 2\\ 3 & 4 & 6\\ \end{matrix} \right]$ 인 경우 $rank(A) = 2$

• row rank : $A$의 행공간에 대한 차원
  

• full rank : $A \in \R^{m \times n}$에 대하여 $rank(A)=min(m,n)$일 때, 즉 $A$의 rank가 $\R^{m \times n}$에 속하는 행렬의 rank 중 가능한 가장 큰 값일 때 $A$는 full rank를 가졌다고 한다. 만약 $A$가 full rank를 가지지 않은 경우, $A$는 rank-deficient하다고 한다. 특히, $A \in \R^{n \times n}$인 정사각행렬일 경우 $A$가 역행렬을 가지기 위해서는 $A$는 반드시 full rank를 가져야만 한다.

• $rank(A) = rank(A^\intercal) = rank(A^\intercal A) = rank(AA^\intercal)$

2. 회고

선형대수를 이용한 미분방정식 풀이는 진짜 대학교에서 무수히 다뤘는데 이게 컴퓨터 공학에서 쓰는 분야가 좀 다른 것 같다. 기저, Span, Basis는 사실 그렇게 중하게 다룬 기억이 없어서 다시 뒤져보는데 시간이 좀 걸렸다. 자만하지 말고, 꼼꼼히 공부해야겠다.