[N534] 내용정리

Sea Panda·2023년 3월 8일

코드스테이츠

부트캠프 TIL

목록 보기

46/46

💡 학습목표

알고리즘 개념을 숲을 보는 시점으로 생각하기.
Dynamic Programming(동적계획법)에 대해 배운다.
Greedy Algorithm(그리디 알고리즘 - 탐욕 알고리즘)에 대해 배운다.

✏️ 알고리즘 설계 기법/ 문제 해결 접근 전략

브루트 포스(Brute Force)
- 무차별 대입 공격, 가능한 모든 조합을 대입해보는 방식
- 예: 네자리 비밀번호를 풀 때 0부터 9999까지 다 넣어보기
분할 정복(Divide and Conquer)
- 문제를 분할(Divide)해서 해결(Conquer)한다.
- 복잡한 문제를 간단한 문제로 나누고, 하위 문제들의 결과를 다시 합쳐서 해결한다.
동적 계획법(Dynamic Programming)
탐욕법(Greedy)

📌 피보나치 수열 문제

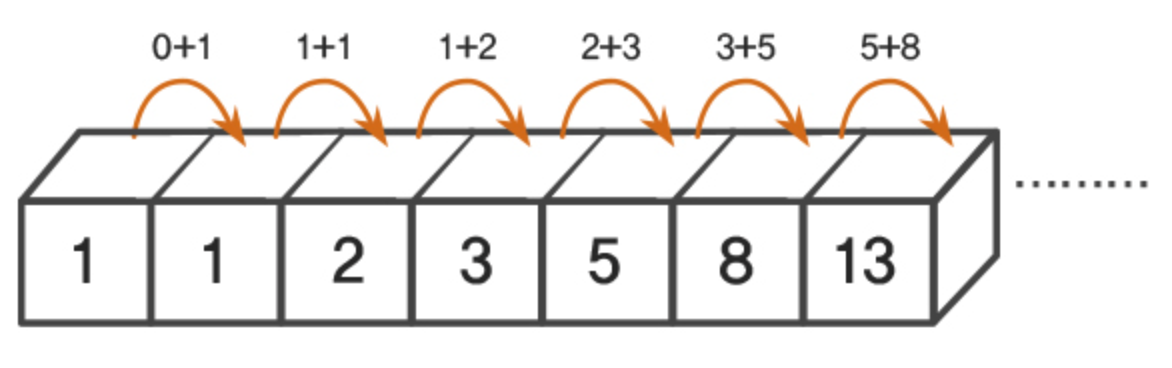
피보나치 수열이란 앞의 두 수의 합이 바로 뒤의 수가 되는 수열을 의미한다. 피보나치 수 $F_n$ 은 다음과 같은 초기값 및 점화식으로 정의되는 수열이다.

F_1 = F_2 = 1\\ F_n = F_{n_1} + F_{n_2}

이 피보나치 수열을 간단하게 재귀함수로 구현하면 다음과 같다.

# 재귀함수로 구현
def fibo(n):
		if n == 1 or n == 2:
				return 1
		return fibo(n-1) + fibo(n-2)
		# 한 줄로도 가능
		# return fibo(n-1) + fibo(n-2) if n >= 2 else n

print(fibo(10))

알고리즘 설계 기법과 문제 해결 접근 전략을 이야기하는데 갑자기 피보나치가 등장해서 의아할 수 있다.

피보나치 수열의 경우 재귀함수를 설명하는데 사용되는 대표적인 문제이다. 하지만 이 코드는 치명적인 단점이 존재하는데, 바로 항이 커질수록 계산속도도 매우 느려진다는 점이다.

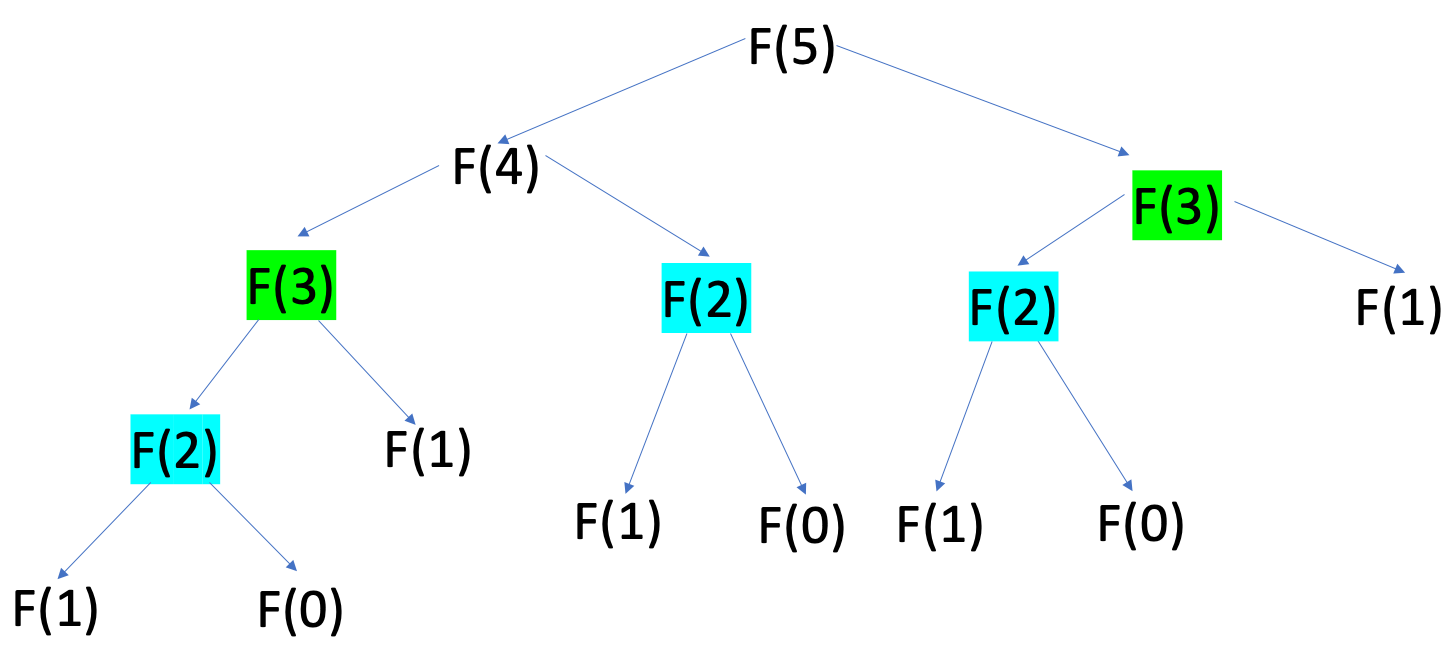
동일한 계산이 반복적으로 수행되며 시간 복잡도는 $O(2^n)$ 이 된다. 이런 문제를 해결하기 위해서 재귀함수로 구성하는 것이 아닌 Dynamic Programming방법을 이용한다면 단점을 보완하며 더 빠른 속도로 문제를 해결할 수 있다.

✏️ Dynamic Programming(동적 프로그래밍)

하나의 문제를 여러 작은 문제로 나누고, 작은 문제의 답을 재사용하여 문제를 효율적으로 푸는 것

기억하며 풀기 또는 기억하기 알고리즘이라고도 할 수 있다.
분할정복과 차이: 문제의 답을 재사용하는 것
- 다이나믹 프로그래밍은 이미 했던 계산은 반복하지 않는다.
- 메모리를 조금 더 사용해서 연산속도를 비약적으로 증가시킨다.(메모리에 계산결과를 저장)
Memoization(메모이제이션), Tabulation(테뷸레이션) 두 가지 방법론이 있다.
"동적"이라는 말에 몰입하여 어느 부분이 동적으로 작동하는지 찾을 필요는 없다. 이 말을 처음 사용한 사람도 그저 이름이 멋있어서 붙인 이름이다.

💡Dynamic Programming의 조건
1. 작은 문제들이 반복된다.
2. 같은 문제는 구할때 마다 정답이 동일하다.

위와 같은 조건을 충족할때만 동적 프로그래밍을 사용할 수 있다. 작은 문제의 결과 값이 항상 같다는 점을 이용해서 큰 문제를 해결하는 방법이니 당연한 것이다.

👉 Memoization(메모이제이션, Top-down(하향식)방식)

메인 문제를 분할하면서 해결하는 하향식 방법(Top-Down)
재귀를 이용하여 값을 위에서 부터 계산한다.
주어진 입력값에 대한 결과를 저장해 같은 입력값에 대해서는 함수가 한 번만 실행된다. -> 함수 실행 횟수 감소
답을 재활용한다는 의미로 동일한 계산을 할 경우 한 번 계산한 결과를 메모리에 저장해 두었다가 꺼내 씀으로써 중복 계산을 방지할 수 있게 하는 기법이다.
이 기법은 메모리라는 공간적 비용을 투입해 시간적 비용을 줄이는 방식이다.

이제 위에서 나온 피보나치 수열문제를 메모이제이션으로 구성하면 다음과 같은 코드가 된다.

# 메모이제이션

def fibo_memo(n):
    # n이 2보다 작거나 같은 경우
    if n <= 2:
        return 1
    else:
        # 계산된 이력이 있는 경우
        if memo_[n] != 0:
            # 해당 함수값 반환하고 호출 종료
            return memo_[n]
        else:
            # f(n) = f(n-1) + f(n-2)
            memo_[n] = fibo_memo(n-1) + fibo_memo(n-2)
            # 결과값 반환 (f(n))
            return memo_[n]

num = 10
# 값 저장용 리스트(계산된 숫자는 해당 숫자의 인덱스에 값이 저장됨)
memo_ = [0]*(num+1)
print(fibo_memo(num))

코드를 보게 되면 계산된 이력이 있는지 살펴보고 없다면 아래의 재귀함수 부분으로 들어가게 된다. 즉 위에서부터(큰 수부터) 계산된 이력이 있는지 파악하면서 작은 수로 내려가기 때문에 하향식 방식이라고 부른다.

위 코드의 시간 복잡도는 $O(n)$ 의 시간복잡도를 가지게 된다.

👉 Tabulation(타뷸레이션, Bottom-Up(상향식) 방식)

가장 작은 문제를 먼저 해결하고 최종적으로 메인 문제를 해결하는 상향식 방법
반복문을 이용해 밑에서부터 계산하기 때문에 memoization과 달리 재귀함수를 사용하지 않는다.
값을 미리 계산해두고 필요하지 않는 값도 미리 계산한다.
- 반복문을 통해 부분 문제에 대한 해답을 하나씩 저장한다.
메모하기 부분에서 Memoization이라고 했는데, Bottom-up(상향식)일때는 Tabulation이라고 부른다.
왜냐하면 반복을 통하여 Dp[0]부터 채우는 과정을 "table-fillint"라고 하며, 이런 방식을 이용하여 작은 문제부터 큰 문제까지 하나하나 테이블을 채워나간다는 의미이다. 근복적인 개념은 결과값을 기억하고 재활용한다는 측면에서 Memoization과 크게 다르지는 않다.

# 태뷸레이션
def fibo_tabul(n):
    # 태뷸레이션 : Botton-Top 방식
    # 0~2번째 값을 먼저 설정
    tab = [0, 1, 1]

    # 3번째 인덱스부터 진행. i번째 자리에 i-1, i-2의 값을 합쳐서 append -> for문
    for i in range(3, n + 1):
        tab.append(tab[i-1] + tab[i-2])

    return tab[n]

print(fibo_tabul(10))

이 코드 역시 시간복잡도는 $O(n)$ 에 해당한다. 하지만 이미 계산된 값을 저장한 리스트에서 값을 가져오는 작업 자체는 $O(1)$ 의 시간 복잡도를 가진다.

두 가지 방법 중 더 다은 것이 있을까?, 하나만 가능한 경우는?

두 방법 중 어느 것이 시간적으로 더 효율적인지 묻는다면, 그에 대한 답은 "알 수 없다"이다.

Top-Down 방식을 사용하는 Memoization은 재귀를 통해 답을 찾아 내려간다. 그렇다보니 재귀함수 호출로인한 Stack이 쌓여서 stackOverFlow같은 에러가 발생할 수 있다. 특히 Python에서는 해당 케이스가 잦다보니 이럴 경우 Bottom-up방식의 Tabulation으로 풀면된다.

두 방법 중 두 가지를 모두 사용하지 못하고 하나만 사용할 수 있는 경우가 있는지에 대해서는 있다고 할 수 있지만 그것은 동적 프로그래밍에 익숙해지고 경험적으로 알아낼 수 있는 부분이라고 한다.

Dynamic programming의 목적

우리가 프로그래밍을 배울 때 항상 기억해야하는 것은 모든 알고리즘은 기존에 있던 문제를 해결하기 위해서 고안되었다는 것이다.

완전 탐색, DFS,BFS와 같은 알고리즘은 수많은 경우의 수를 전부 따져봐야 하는데 그 경우의 수가 너무 많아서 속도가 느려지는 문제를 개선하고자, 수행 시간을 단축하고자 만들어진 알고리즘이 Dynamic programming이다.

💡 Dynamic Programming의 유형

DFS/BFS로 풀 수 있지만 경우의 수가 너무 많을 때

패턴을 파악하여 경우의 수가 얼마나 증가할지 고려

DFS나 완전 탐색으로 진행하는 maginot line은 500만 개의 경우의 수로 볼 수 있다.

$5*10^6$ 을 넘어가는 경우의 수라면 동적 프로그래밍방법 사용을 고려해 볼 것.

경우의 수들에 중복적인 연산이 많은 경우

DP를 사용하게 되는 상황: 이진 검색, 최단경로 알고리즘, 최적화 문제, 외판원 문제

Dynamic Programming과 분할정복

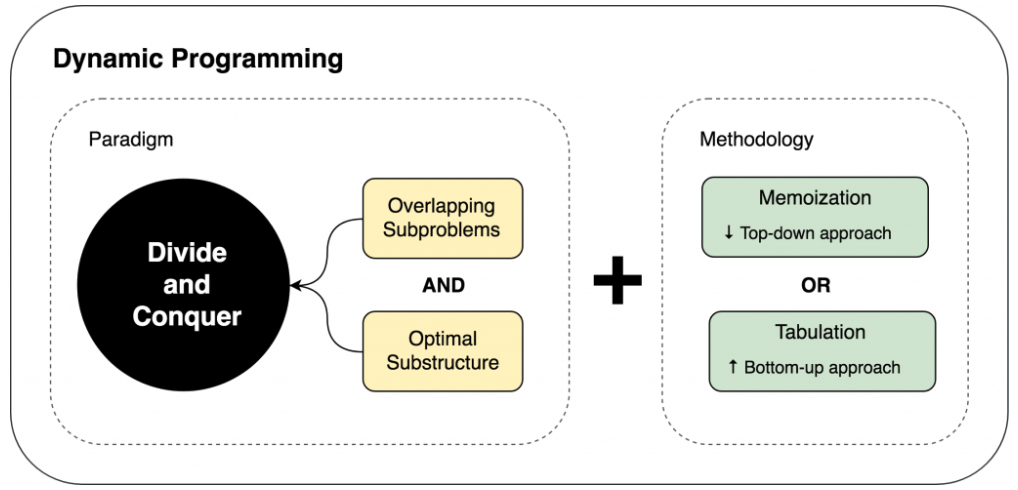
DP는 분할정복에 다음과 같은 개념이 추가된 것이라고 할 수 있다.
- 중복된(반복되는) 서브문제(Overlapping Subproblems)
  - 메인과 서브문제를 같은 방법(반복)으로 해결할 수 있어야 한다.(문제해결관점)
- 최적 부분 구조(Optimal Substructure)
  - 메인문제 해결방법을 서브문제에서 구하여 재사용하는 구조여야 한다.(문제의 구조관점)

👉 정리: DP는 최적 부분 구조로 구성된 중복된 서브문제를 분할정복으로 해결한다.

Greedy Algorithm(탐욕법)

뒤는 생각하지 않고 오로지 매 순간 현재 최선인 답을 선택하여 최종적으로 최적값, 또는 근사값을 구하는 방법

중복되지 않는 서브문제를 더 빨리 풀 수 있는 방법론이다.
매 순간 현재 최선인 답을 선택해서 최종적으로 최적값, 또는 근사값을 구한다.
- 전체에서 최적값(가장 좋은 결과)을 항상 보장하지는 않는다.
- 코드 작성이 쉽고 연산 시간도 빠르다.
- 완벽한 베스트는 구하지 못하더라도 최악의 결과는 아닐 수 있다.
탐욕 알고리즘은 모든 경우의 수를계산하는데 시간이 오래 걸리거나 방법이 복잡한 경우 간단한 방법으로 비교적 빠르게 최적의 결과 또는 최적의 근사값을 얻을 수 있을 때 주로 사용한다.
그리디 알고리즘 문제는 문제를 푸는 것보다 문제 파악이 더 어려울 때가 많다.
- 어떤 문제가 주어지면 문제를 파악하는 능력과 함께 어떤 알고리즘이 가장 효율적인지 알아내는 것은 매우 중요하다. 어떤 알고리즘이 효율적인지 알아내는 것은 직관에 의존하기 때문에 문제를 많이 풀어봐야 한다.
Greedy Algorithm은 특별한 코드가 있는 알고리즘이 아닌 개념적인 알고리즘이다. 어떠한 문제에도 적용할 수 있지만, 문제마다 적용하는 방식은 모두 다르다.
Greedy Algorithm에서 가장 어려운 점은 다음과 같다.
- 이 문제에 Greedy Algorithm을 써야 할지 다른 알고리즘을 써야할지 알아내는 것.
- Greedy Algorithm적용 시 최선의 선택 기준을 어떻게 알아내느냐 하는 것.

모든 경우의 수를 확인하는 방법(=무차별 대입)을 Brute-Force(브루트 포스)방법이라고 한다. 무차별 대입법은 알고리즘이라고 불리기는 조금 민망하지만, 모든 경우의 수를 일일이 확인하기 때문에 시간을 오래 걸려도 정답을 확실히 찾을 수 있다는 장점이 있다.

Greedy Algorithm 언제 사용할까?

Greedy Algorithm은 크게 2가지 경우에서 사용한다.

Greedy Algorithm으로 최적의 해를 찾을 수 있는 경우
Greedy Algorithm은 다른 알고리즘에 비해 코드를 쉽게 작성할 수 있고 처리 속도 또한 뛰어나다.

최적의 해를 계산하는데 시간이 오래걸리는 문제에 대해 Greedy Algorithm을 이용하면 적당히 빠르면서 괜찮은 근사해를 구할 수 있는 경우

💡 풀이 방식
기본적으로 그때그때 가장 좋은 해결책을 찾아가는 기법이다. 해를 구하는 일련의 선택과정 마다 가장 좋아보이는 최선을 선택하면, 전체적으로 최적 해를 구할 수 있다는 방법론이다. 각 단계마다 최상으로 보이는 해결핵으로 구한 해들을 모아서 제시하게 된다.

💡 적용문제

동전 거스름돈을 가장 적은 수의 동전으로 주는 문제

최단경로 알고리즘(다익스트라 알고리즘)

최소비용 신장트리(Spanning Tree)를 구하는 알고리즘(크루스칼 알고리즘, 프림 알고리즘 등)(참고)

# 탐욕 알고리즘 예제: 잔돈
# 잔돈갯수를 구하자.(갖고 있는 돈 : 100원)
price = int(input('물건값을 입력하세요.'))

# 거스름돈
change = 100 - price
print(f'잔돈은 {change}원입니다.')

coin_list = [50, 40, 20, 10, 5]   # 받을 수 있는 잔돈의 종류. 크기순으로 적는다.(중요)

change_count = []   # 잔돈갯수

while change != 0:
    for coin in coin_list:
        change_bool = 0 # (동전 종류마다)동전 갯수에 대한 변수 생성
        # Greedy: 우선 금액이 큰 동전부터 거슬러준다.
        change_bool = change_bool + (change // coin)  # 몫이 동전의 갯수.
        print(change_bool)
        change_count.append(change_bool) # 잔돈 갯수 리스트에 추가
        change = change - (change_bool * coin) # 잔돈 갱신
        print(coin, change_count)
        
print('잔돈갯수 :',sum(change_count)) # 잔돈의 갯수를 합한다.(sum 내장함수 활용)

DP와 Greedy

최적 부분 구조 문제를 푼다는 점에서 비교된다.
- Dynamic programming
  1. 문제를 작은 단위로 분할하여 해결한 후, 해결된 중복문제들의 결과를 기반으로 전체문제를 해결한다.
- Greedy
  1. 각 단계마다 최적해를 찾는 문제로 접근한다.
  2. 해결해야 할 전체 문제의 갯수를 줄이기 위해서 개별적으로 문제를 해결해나가는 선택을 한다.

❗️ 참고자료
1. 코드스테이츠 교육자료

Sea Panda

이전 포스트