[AI] 과적합(Overfitting), 오차 역전파(Error Backpropagation), 경사하강법(Gradient Descent)

과적합(Overfitting)

• 학습 데이터에 맞춰 최적화되어 전체 특성에서 벗어나는 문제
  

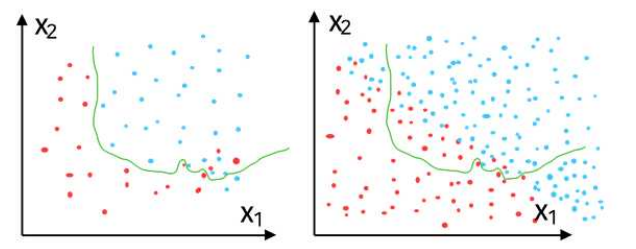
  • 왼쪽 데이터: 샘플링을 해 온 학습 데이터

  • 학습 데이터에서 성능이 최대한 잘 나오도록 알고리즘을 학습시켜보면 왼쪽처럼 구분선이 그려짐

  • 이 구분선을 이용해 실제 데이터에 적용해보면 적중률이 떨어지는 경우가 있음
    (학습 데이터가 실제 데이터를 충분히 반영하지 못 했을 경우)

    
    

  과적합 어떻게 해결해?

1. 학습 데이터를 더 많이 수집
2. Feature의 개수를 줄임
   (ex, 100개의 데이터를 학습한 경우, 50개로 테스트)
3. 정규화(Regularization)

   • 데이터를 구분하는 선이 지나치게 구불구불해지지 않게 막아줌

   • 최대한 직선에 가깝게 곡률을 줄여주는 역할을 하는 factor를 cost함수에 추가해줌

   • 이 식은 정규화를 수행하지 않기 때문에, Overfitting 발생 가능성 있음
     

     
     

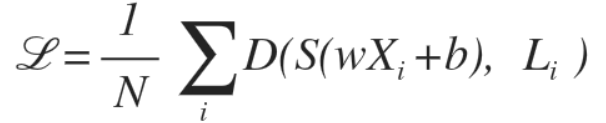
   • 아래 식 처럼 최대한 구분선이 구불구불하지 않도록 펴 주는 Regularization Strength를 추가해주면 된다.
     

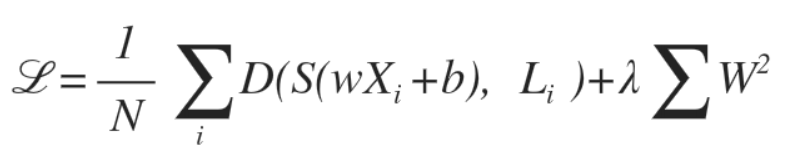
     • λ(람다) 값에 의해 얼마나 필 것인지를 결정함
       (너무 크게 하면 정확도가 떨어질 수 있음)

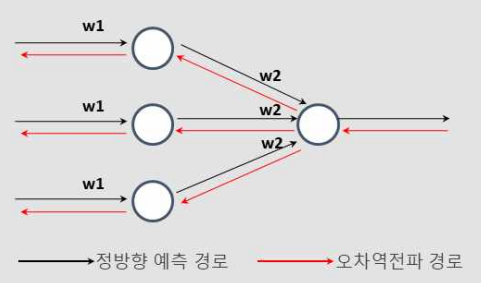
오차 역전파(Error Backpropagation)

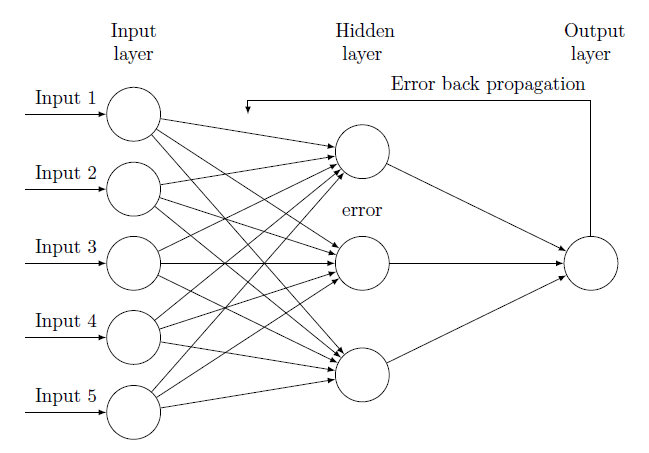
• input에서 output 방향으로 가중치를 업데이트 하며 활성화 함수를 통해 결과값을 가져오게 됨

• 이러한 방법이 순전파(foward)임

• But, 임의로 설정한 가중치 값이 업데이트 되긴 했지만 정확하지 않을 수 있음

▶️ 역전파 방법을 사용하자!!

• 결과값을 통해서 다시 역으로 input방향으로 오차를 다시 보내며 가중치를 재 업데이트

• 오차(error)를 다시 역방향으로 보내면서 가중치를 게산하여 오차를 적용시킴

• 한 번 돌리는 것을 1 epoch 주기 라고 함!

• epoch 값을 늘릴 수록 가중치가 계속 업데이트(학습) 되면서 점점 오차가 줄어나가는 방법임!

경사 하강법(Gradient Descent)

자세한 내용은 이 글 참고
[딥러닝] Gradient Descent(경사 하강법), Gradient-Based Optimization 기초부터 자세하게

함수의 기울기(경사)를 구하여 기울기가 낮은 쪽으로 계속 이동시켜서
극값에 이를 때까지 반복시키는 것

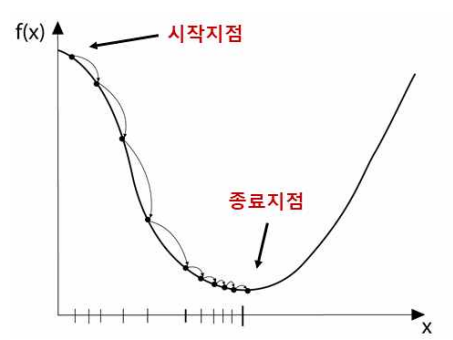
• 함수 값이 낮아지는 방향으로 독립 변수 값을 변형시켜가면서 최종적으로는 최소함수의 값을 갖도록 하는 독립 변수의 값을 찾는 방법

뭐야.. 최소값 찾을거면 그냥 미분하면 되는거 아님?

• 실제 분석에 사용되는 함수는 닫힌형태가 아니거나,
  함수의 형태가 복잡(비선형..같은놈)해서 미분계수와 그 근을 계산하기 어려운 경우가 많음

• 미분계수를 계산하는 과정을 컴퓨터 구현하는 것보다 gradient descent는 더 쉽게 구현 가능함

• 데이터의 양이 매우 많은 경우 gradient descent와 같은 반복적인 방법을 통해 해를 구하면 계산량 측면에서 더 효율적임!

경사하강법 공식

기울기가 양수라면 음의 방향으로 x를 옮기고, 음수면 양의 방향으로 옮기면 됨

$x_{i+1} = x_i - \text{이동 거리} \times\ \text{기울기의 부호}$

이동거리는 어떻게?

• 미분계수는 극소값에 가까워질수록 값이 작아짐
• So, 이동거리에는 미분계수와 비례하는 값을 이용!
• 극소 값에서 멀때는 많이 이동하고, 극소값에 가까울 때는 조금씩 이동하는 원리임
  

$x_{i+1} = x_i - \alpha \frac{df}{dx}(x_i) \; ( 단, \alpha = \text{step size})$

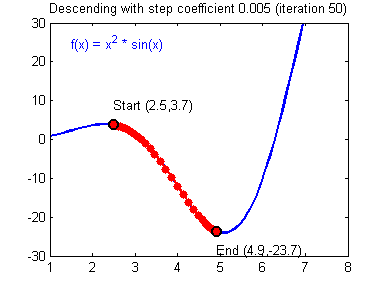
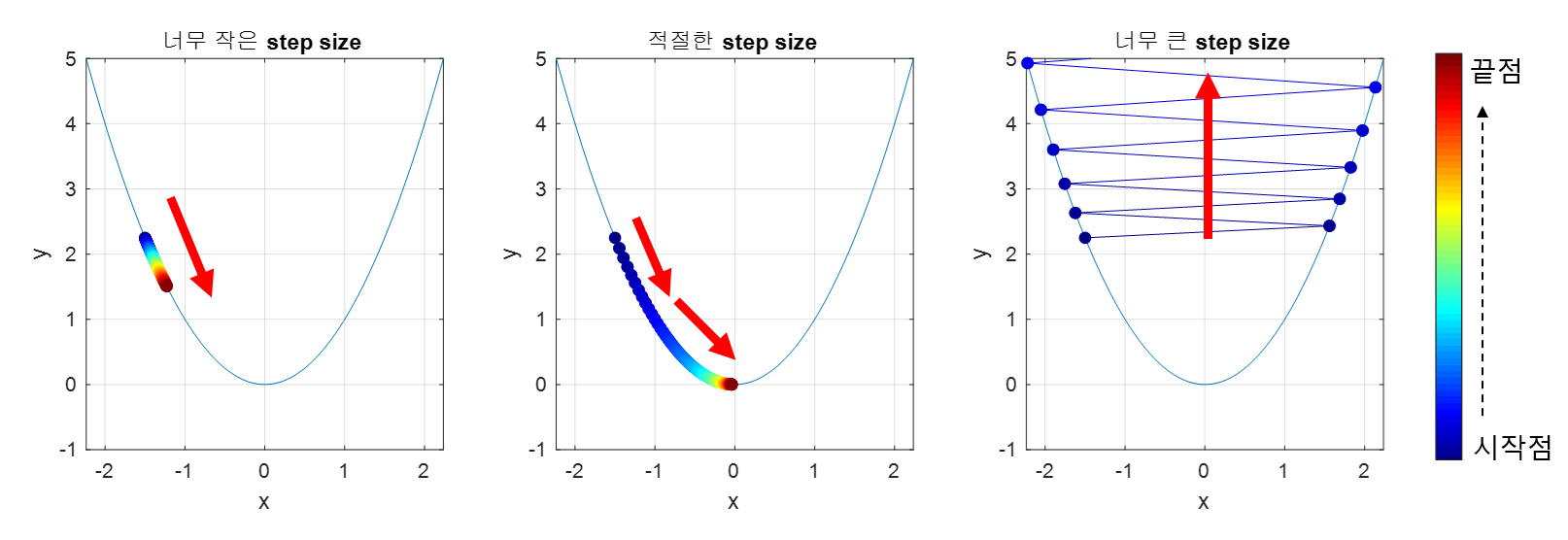
Step size 어떻게 선택함?

step size가 큰 경우 이동거리가 커지므로 빠르게 수염할 수 있다는 장점이 있지만,
최소값으로 수렴되지 못하고 함수 값이 발산할 여지가 있다.

step size가 너무 작으면 발산하지는 않겠지만, 최소 값을 찾는데 너무 오래걸릴 수도..

경사하강법의 문제점, Local Minima

• 우리가 찾고 싶은 것은 global minimum 인데,
• 어떤 경우에는 local minima에 빠져 벗어나가지 못하는 상황이 발생하기도 함..

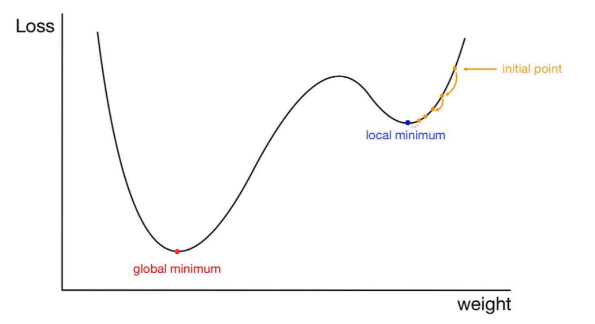
그치만 실제로 딥러닝이 수행될 때 local minima 에 빠질 확률은 거의 없음~

• local minima문제는 사실 상 고차원 공간에서 발생하기 힘든 현상이기 때문

• 실제 딥러닝 모델에서는 엄청난 수의 가중치가 있는데, 이 가중치들이 모두 local minima에 빠져야 가중치 업데이트가 정지 되기 때문에 사실 상 큰 문제는 없음!

• 고차원 공간에서의 critical point는 대부분 saddle point임

• local minima가 발생한다 해도 이는 사실 global minimum이거나 그와 유사한 에러 값을 가져 문제가 되지 않음

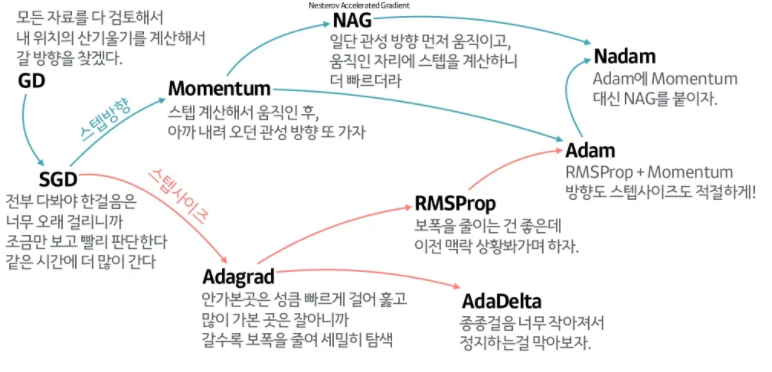
ref

https://zsunn.tistory.com/entry/AI-DNNDeep-Neural-Network%EC%9D%98-%EC%9D%B4%ED%95%B4-%EB%B0%8F-%EC%8B%A4%EC%8A%B5
http://contents2.kocw.or.kr/KOCW/data/document/2020/edu1/bdu/hongseungwook1118/031.pdf
https://ebbnflow.tistory.com/119
https://m.blog.naver.com/PostView.nhn?blogId=complusblog&logNo=221243306163&proxyReferer=https:%2F%2Fwww.google.com%2F
https://sacko.tistory.com/19
https://angeloyeo.github.io/2020/08/16/gradient_descent.html
https://variety82p.tistory.com/entry/Local-Minima-%EB%AC%B8%EC%A0%9C%EC%97%90%EB%8F%84-%EB%B6%88%EA%B5%AC%ED%95%98%EA%B3%A0-%EB%94%A5%EB%9F%AC%EB%8B%9D%EC%9D%B4-%EC%9E%98-%EB%90%98%EB%8A%94-%EC%9D%B4%EC%9C%A0%EB%8A%94
https://www.slideshare.net/yongho/ss-79607172/49