
DNN(Deep Neural Network): 심층 신경망
Deep Neural Network
- DNN은 입력층과 출력층 사이에 여러개의 은닉층(hidden layer)들로 이루어진 인공신경망
- 컴퓨터가 스스로 분류 레이블을 만들어 내고 공간을 왜곡하고 데이터를 구분짓는 과정을 반족하여 최적의 구분선을 도출
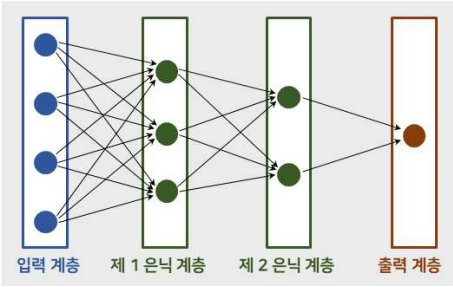
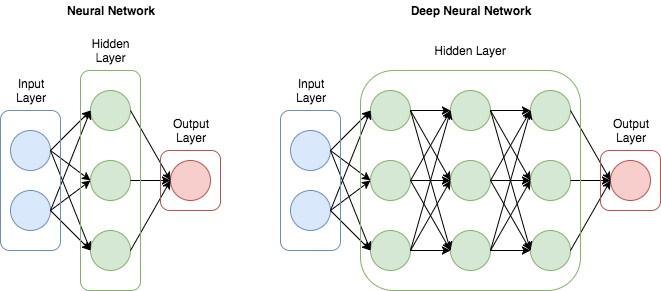
- 복잡한 비선형(non-linear) 관계도 모델링 할 수 있음
- 사물 식별 모델을 위한 심층 신경망 구조에서는 각 객체가 이미지 기본 요소들의 계층적 구성으로 표현될 수 있음
- 이때, 추가 계층들은 점진적으로 모여신 하위 계층들의 특징들을 규합시킬 수 있음
- 이러한 특징은, 비슷하게 수행된 ANN에 비해 더 적은 수의 유닛(unit, node)들 만으로도 복잡한 데이터를 모델링 할 수 있게 해줌!!!
심층 신경망은 표준 오류역전파 알고리즘으로 학습될 수 있음!!
이 때, 가중치(weight)들은 아래의 등식을 이용한 확률적 경사하강법을 통해 갱신될 수 있음!
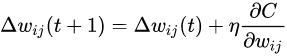
-
η = 학습률(learning rate)
C = 비용함수(cost function) -
비용함수의 선택은
학습의 형태(지도 학습, 자율 학습 (기계 학습), 강화 학습 등)와활성화함수(activation function)같은 요인들에 의해서 결정됨. -
예를 들면, 다중 클래스 분류 문제(multiclass classification problem)에 지도 학습을 수행할 때, 일반적으로 활성화함수와 비용함수는 각각 softmax 함수와 교차 엔트로피 함수(cross entropy function)로 결정된다.
DNN의 장점 👍
- 연속형, 범주형 변수에 상관없이 모두 분석 가능
- 입력 변수들 간의 비선형 조합이 가능
- 예측력이 다른 머신러닝 기법들에 비해 상대적으로 우수한 경우가 많음
- feature extraction이 자동으로 수행되어, 변수 선택의 번거로움을 줄여줌
- 데이터양이 많아질수록 성능 좋아짐
DNN의 단점 😖
- 신경망이 복잡할 경우 작동하는데 시간이 오래걸림
- GPU가 장착된 고사양의 컴퓨터가 필요...
- 분석 시 변수들을 일정한 순서나 방식으로 넣는 것이 아니기 때문에 결과가 일정하지 않음
- 가중치의 의미를 정확하게 해석하기 어렵기 때문에 결과 해석이 어려움
- 과적합에 취약함...
- 추가된 계층들이 학습 데이터의 rare dependency의 모형화가 가능하도록 해주기 때문
- 과적합을 극복하기 위해 weight decay (l2–regularization) 또는 sparsity (l1–regularization) 와 같은 regularization 방법들이 사용될 수 있음
- 최근에는 dropout정규화가 등장!!
: 학습 도중 은닉 계층들의 몇몇 유닛들이 임의로 생략되어, 학습 데이터에서 발생할 수 있는 rare dependency를 해결하는데 도움을 줌
ref
http://www.tcpschool.com/deeplearning/deep_algorithm1
https://ko.wikipedia.org/wiki/%EB%94%A5_%EB%9F%AC%EB%8B%9D
https://www.todaymart.com/631
