DNA 서열
- DNA는 A, T, C, G의 4가지 염기로 구성되어 있으며 A-T, C-G의 연결이 존재한다.
DNA 돌연변이
- 교환 돌연변이 : 핵염기가 서로 바뀐다.
- 삽입 돌연변이 : 핵염기쌍이 추가된다.
- 제거 돌연변이 : 핵염기쌍이 제거된다.
동족 서열
- 하나의 종에서 출발하여 DNA 돌연변이로 인하여 DNA 서열이 달라지며 달라진 두 종에서 추출한 염기 서열을 동족 서열이라고 정의한다.
- 달라진 두개의 염기서열을 맞추는 최적의 알고리즘이 필요하다.
DNA 서열 최적의 맞춤
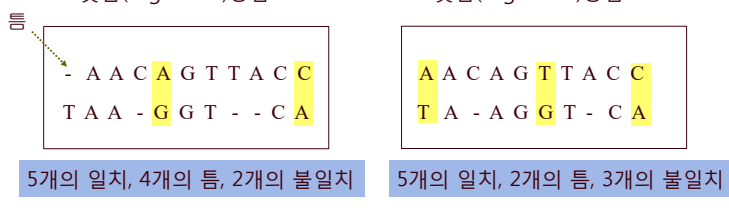
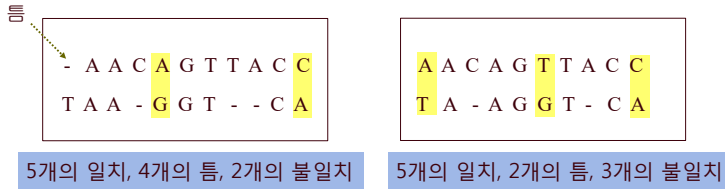
- 각각의 DNA 서열을 비교하여 불일치 되는 부분과 틈의 부분의 손해를 정의한 후 손해가 최소가 되는 방법으로 서열을 최적화한다.
Gap
- 위치에서 제거가 일어났거나 상대편 서열에 삽입이 발생했다는 것을 의미한다.
동적계획식 설계 절차
- 각각의 길이가 n과 m인 염기 서열이 있다고 할 때
- opt(i,j)는 부분서열 x[i ... n]과 y[j ... m]의 최적 맞춤 비용이라고 정의하며,
- opt(0, 0)은 모든 염기설열의 최적 맞춤 비용으로써 구하고자 하는 최종 값이다.
최적화 식
- 틈의 손해 비용을 2, 불일치의 손해 비용을 1이라고 정의하면,
- 구하고자 하는 최종 값이 opt(0, 0)은 4가지 경우로 나눌 수 있다.
- x[0]과 y[0]이 일치하는 경우
- x[0]과 y[0]이 불일치하는 경우
- x[0]에 틈을 입력하는 경우
- y[0]에 틈을 입력하는 경우
- 따라서 opt(0,0) = min(opt(1, 1) + penalty, opt(1,0) + 2, opt(0, 1) + 2)로 표현할 수 있다.
- penalty = 0 (if x[0] = y[0])
- penalty = 1 (if x[0] != y[0])
재귀 알고리즘 구축을 위한 종료 조건
-
서열 x의 크기를 m, 서열 y의 크기를 n이라고 하면,
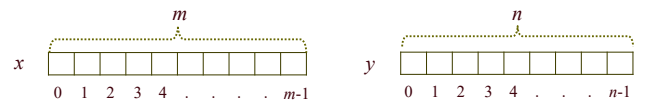
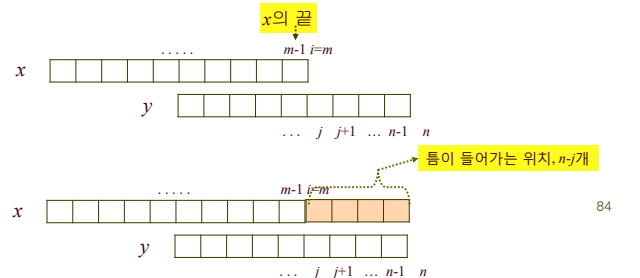
-
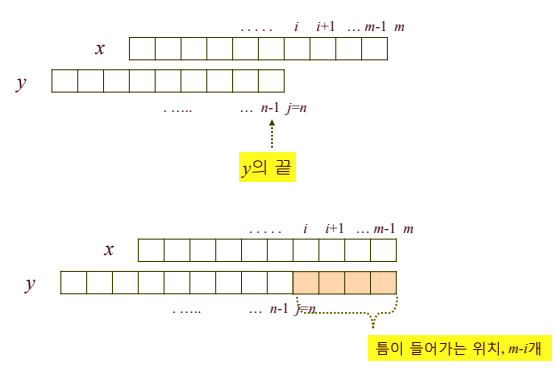
서열 x의 끝지점을 지났고(i=m), 서열 y의 j지점(j<n)에 있다면, 틈을 n-j개 삽입해야 한다.
따라서, opt(m,j)=2(n-j)
- 서열 y의 끝지점을 지났고(j=n), 서열 x의 i지점(i<m)에 있다면, 틈을 m-i개 삽입해야 한다.
따라서, opt(i,n)=2(m-i)
분할 정복 방법 - pseudo code
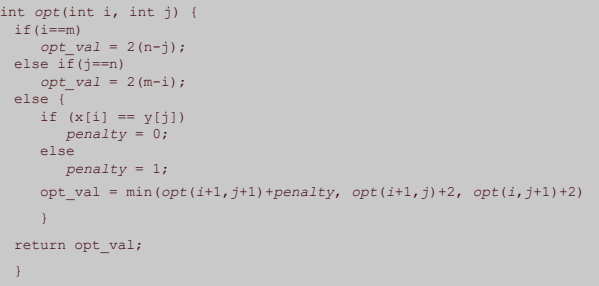
- 분할 정복 방법을 사용하면 같은 함수를 중복해서 호출하기 때문에 매우 비효율적이다.
동적 계획식 최적 맞춤 방법
-
각각의 서열을 x, y축으로 두고 마지막 행, 마지막 열에 틈 문자를 추가하여 기록한다.
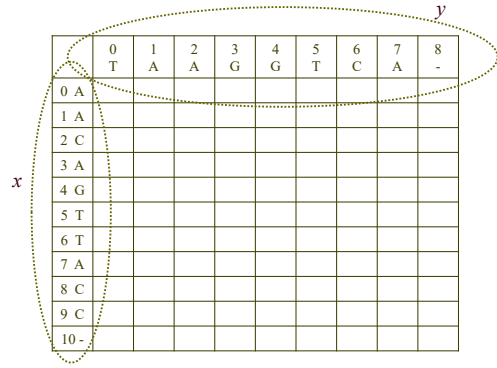
-
틈행과 틈열을 채운다.
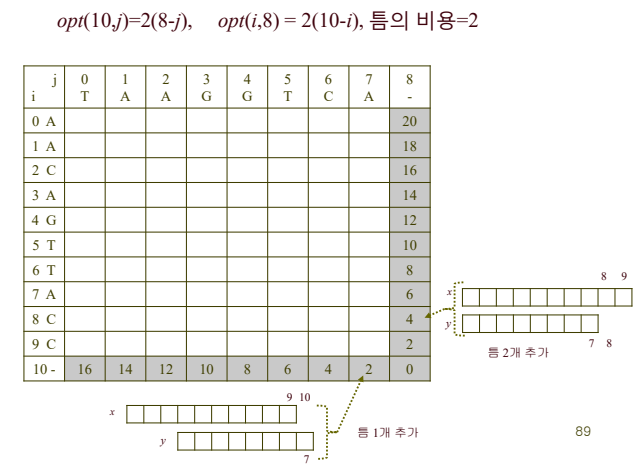
-
우측 아래부터 대각원소들을 채워넣는다.
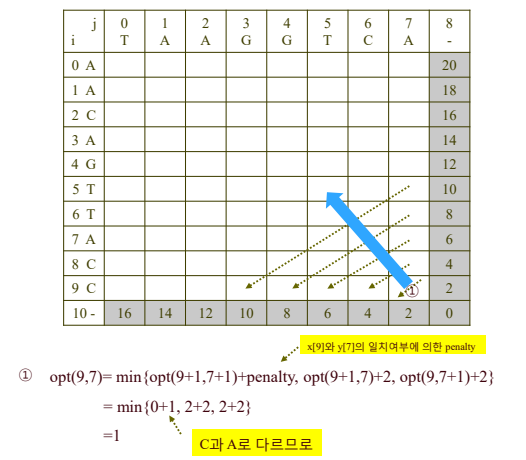
최적 서열맞춤을 찾아가는 방법
- 테이블에 모든 요소를 채운뒤 [0][0]을 선택한다.
- 최적화 식 opt(0,0) = min(opt(1, 1) + penalty, opt(1,0) + 2, opt(0, 1) + 2) 을 이용하여 [0][0]을 도출시킬수 있는 이전 단게의 값을 최적 서열에 삽입한다.
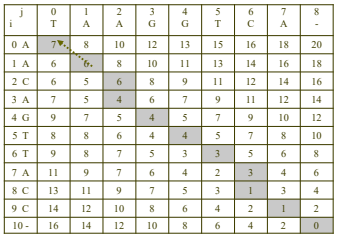
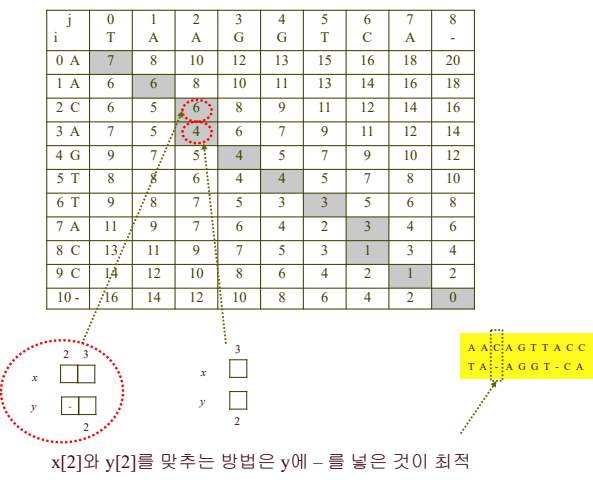
- 최적 배열의 오른쪽 아래에서부터 구성을 시작하여 표시해둔 경로를 따라 최적 염기 서열을 구성한다.
- 최적 경로가 위로 이동한다면 x서열에 해당 염기를 입력하고 y서열에 틈문자를 입력한다.
- 최적 경로가 왼쪽으로 이동한다면 x서열에 틈문자를 입력하고 y서열에 해당 염기를 입력한다.
python code
def printmatrixf(mat):
# 행렬의 형태로 출력을 위한 함수
row = len(mat[0])
col = len(mat)
for i in range(col):
for j in range(row):
print(f'{mat[i][j]:>3.2f}', end=' ')
print()
def printmatrix(mat):
row = len(mat[0])
col = len(mat)
for i in range(col):
for j in range(row):
print(f'{mat[i][j]:>3}', end=' ')
print()
def dna_alignment(a, b):
m = len(a) # 행의 개수로 사용될 변수의 값을 할당합니다.
n = len(b) # 열의 개수로 사용될 변수의 값을 할당합니다.
table = [[0 for _ in range(0,n+1)] for _ in range(m+1)]
minindex = [[(0,0) for _ in range(n+1)] for _ in range(m+1)]
# table, minindex의 2차원 배열에 (m+1) * (n+1)의 영행렬의 생성합니다.
for j in range(n-1, -1, -1):
table[m][j] = table[m][j+1] + 2
for i in range(m-1, -1, -1):
table[i][n] = table[i+1][n] + 2
# 가장 우측하단의 0의 원소로부터 위, 왼쪽으로 갈때마다 2가 증가한 값을 더합니다
# dna의 길이가 맞지 않을 때 틈을 넣음으로써 2의 penalty값을 갖는 것을 의미합니다.
for i in range(m-1, -1, -1):
for j in range(n-1, -1, -1):
penalty = 0
if a[i] != b[j]:
penalty = 1
table[i][j] = min(table[i+1][j+1] + penalty, table[i+1][j] + 2, table[i][j+1] + 2)
# 가장 끝부터 비교하여 a 또는 b에 틈이 있는 경우, 또는 불일치, 일치되는 경우를 가정하고,
# 그 중에서 가장 penalty가 적은 값을 table의 요소로 저장합니다.
if table[i][j] == table[i + 1][j + 1] + penalty: # 불일치
minindex[i][j] = (i + 1, j + 1)
elif table[i][j] == table[i + 1][j] + 2: # 틈
minindex[i][j] = (i + 1, j)
else:
minindex[i][j] = (i, j + 1)
# minindex의 (i,j)요소에는 오른쪽, 아래, 대각선 아래 방향의 3가지 방향에서의
# 최소값과 일치하는 (x,y) 값을 할당함으로써 어떤 경우가 최적화를 이루는 방식인지 지칭합니다.
printmatrix(table)
print()
x, y = 0, 0
while x < m and y < n:
tx, ty = x, y
print(minindex[x][y])
(x, y) = minindex[x][y]
if x == tx + 1 and y == ty + 1: # 일치 또는 불일치의 경우
print(a[tx], " ", b[ty])
elif x == tx and y == ty + 1: # a의 data에 틈이 발생한 경우
print(" - ", " ", b[ty])
else: # b의 data에 틈이 발생한 경우
print(a[tx], " ", " -")