Algorithm - 분할정복법 - binary search & mergesort

분할정복식 설계전략

• Top-Down(하향식) 방법

분할

• 해결하기 쉽도록 문제를 여러 개의 작은 부분으로 나눈다.

정복

• 나눈 작은 문제를 각각 해결한다.

통합

• 해결된 해답을 모은다.

이분 검색 적용

pseudo code

설계 전략

• 찾고자 하는 키값을 기준으로 절반의 범위인 작은 부분으로 계속하여 나눈다.

시간 복잡도 분석 (최악의 경우)

• 배열 아이템의 개수가 짝수인 경우, 검색 배열의 크기가 항상 n/2가 되는 경우
  
  

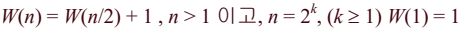
• 일반적인 경우 : 반쪽 배열의 크기가 floor(n/2)
  

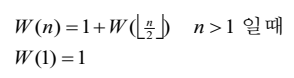
python

import random

class data:
    def __init__(self, n=0):
        self.n = n
        self.elem = self.make_data(self.n)
        self.compare_count = 0

    def make_data(self, n):
    # data(n)으로 객체가 생성되면 1~n까지의 임의의 수를 n개 생성하고 비내림차순으로 정렬합니다
        elem = []
        for i in range(n):
            elem.append(random.randint(1, n))
        elem = sorted(elem)
        return elem

    def location(self, item, low, high):
        # low가 high값보다 커진 경우, 마지막으로 비교한 후
        # index값으로 'not found'의 의미로 -1을 반환하며
        # 데이터 수에 대한 비교 회수를 측정하기 위하여 self.compare_count값을 반환합니다.
        if low >= high:
            self.compare_count += 1
            return -1, self.compare_count
        else:
            mid = int((low + high) / 2)
            if item == self.elem[mid]:
            # 찾고자 하는 값을 데이터 내에서 찾은 경우 비교횟수를 증가한 후
            # 찾고자 하는 값의 데이터 내의 index번호와 비교 횟수를 반환합니다.
                self.compare_count += 1
                return mid, self.compare_count
            elif item < self.elem[mid]:
            # 찾고자 하는 값이 데이터의 중앙값보다 작을 경우, 데이터의 앞 절반으로 범위를 축소합니다
                self.compare_count += 1
                return self.location(item, low, mid - 1)
            else:
            # 찾고자 하는 값이 데이터의 중앙값보다 클 경우, 데이터의 뒤 절반으로 범위를 축소합니다
                self.compare_count += 1
                return self.location(item, mid + 1, high)

    def binsearch(self, x):
        index, compare = self.location(x, 0, self.n)
        return index, compare

if __name__ == '__main__':
    aver = 0
    for i in range(1000):
        x = data(128)
        ranint = random.randint(1, 128)
        index, compare = x.binsearch(ranint)
        aver += compare
    print("데이터의 개수가 128개일 때 평균적으로 : ", aver/1000,"번 비교를 수행합니다")

    aver = 0
    for i in range(1000):
        x = data(256)
        ranint = random.randint(1, 256)
        index, compare = x.binsearch(ranint)
        aver += compare
    print("데이터의 개수가 256개일 때 평균적으로 : ", aver/1000,"번 비교를 수행합니다")

    aver = 0
    for i in range(1000):
        x = data(512)
        ranint = random.randint(1, 512)
        index, compare = x.binsearch(ranint)
        aver += compare
    print("데이터의 개수가 512개일 때 평균적으로 : ", aver/1000,"번 비교를 수행합니다")


    print("이분 검색시 데이터의 개수가 2배 증가할 때 마다 평균 비교 회수가 약 1회 증가합니다")
    print()

합병 정렬 적용

pseudo code

설계 전략

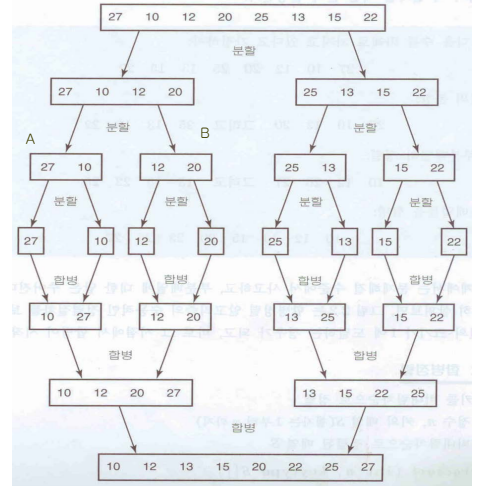
• 정렬이 가능하도록 다루기 쉬운 크기로 분할 후 차례차례 정렬한 후 합병한다.
  

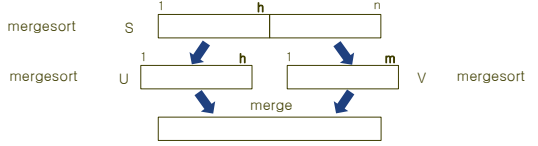
합병

최악의 경우 시간복잡도 분석

배열 u와 v에 들어 있는 아이템의 개수가 각각 h와 m이라고 할 때,

• 단위 연산 : u[i]와 v[j]의 비교 횟수
• 최악의 경우 : v에 있는 m - 1개의 항목이 배열의 앞에 위치하고 그 다음에 u의 아이템이 배열에 들어 있는 경우
  ex) u : 4, 5, 6, 7 v : 1, 2, 3, 8
• 시간 복잡도 : W(h, m) = h + m - 1
  
  
• 단위 연산 : 합병 알고리즘 merge에서 발생하는 비교 횟수
  
  

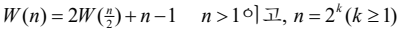
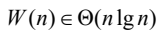
공간 복잡도 분석

• 추가적인 저장 장소를 사용하지 않는 제자리 정렬(in-place sort) 알고리즘이라고 정의한다.
• 합병 정렬은 기존의 배열 외에도 u와 v의 추가적인 배열의 공간이 필요하므로 제자리 정렬 알고리즘이 아니다.
• 하단의 재귀 호출이 종료될 때까지 상위의 재귀호출이 생성하는 공간이 유지되어야 한다.

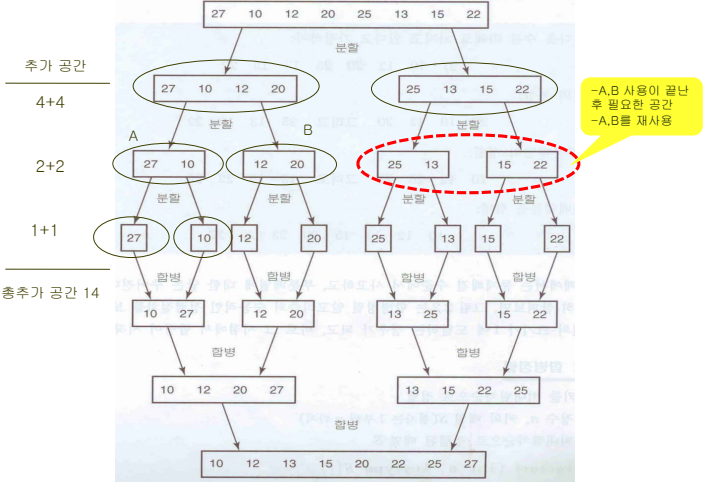
합병정렬에 필요한 추가적인 공간

• mergesort를 재귀호출할 때마다 배열 크기의 반이 되는 공간이 추가적으로 필요하다.
  

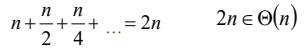
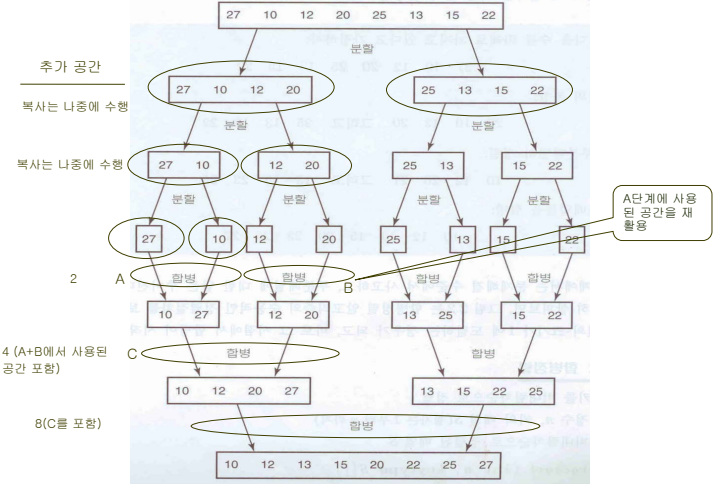
• 합병 정렬을 진행하면서 앞의 단계에서 사용한 배열을 중복적으로 사용하는 방법을 통하여 공간 복잡도가 n이 되도록 향상시킬 수 있다.
  
  

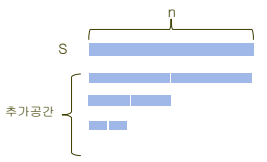
공간복잡도가 향상된 합병정렬 알고리즘

python

def merge(left_length, right_length, left, right, data):
    i, j, k = 0, 0, 0
    while i < left_length and j < right_length:
        # 분할된 두 개의 데이터에서 더 작은 값을 가지는 것부터 전체 데이터의 앞의 값으로 채웁니다.
        if left[i] <= right[j]:
            data[k] = left[i]
            i += 1
        else:
            data[k] = right[j]
            j += 1
        k += 1
    if i >= left_length:
        # 분할된 2개의 데이터에서 왼쪽의 요소가 모두 비교가 끝났다면
        # 전체 데이터에 오른쪽의 요소를 차례로 첨가합니다.
        for a in range(j, right_length):
            data[k] = right[a]
            k += 1
    elif j >= right_length:
        # 분할된 2개의 데이터에서 오른쪽의 요소가 모두 비교가 끝났다면
        # 전체 데이터에 왼쪽의 요소를 차례로 첨가합니다.
        for b in range(i, left_length):
            data[k] = left[b]
            k += 1


def merge_sort(data_length, data):
    global size, max_space
    # 재귀적으로 호출될 때마다 새로 값을 할당하지 않기 위해서 전역변수로 설정합니다.

    left_length = int(data_length/2)
    right_length = data_length - left_length

    if data_length == 1:
        max_space = True
    # 절반의 데이터가 1개의 데이터만 가질 때까지 분할될 때는, 공간을 반납하기전
    # 병합정렬이 추가적으로 필요한 저장공간의 최대치일때입니다.
    # 데이터의 요소가 1개일 시점을 변곡점으로 삼아 추가적인 최대 공간 크기를 더 계산하지 않기 위해 지정합니다.

    if data_length > 1:
        left = data[:left_length]
        right = data[left_length:]
        if not max_space:
            size += (len(left) + len(right))
        merge_sort(left_length, left)
        merge_sort(right_length, right)
        # 1개의 요소를 가질 때까지 재귀적으로 호출하며 분할합니다.
        merge(left_length, right_length, left, right, data)
        # 1개의 요소까지 분할되었다면 차례로 크기를 비교하고, 합병하며 정렬합니다.

if __name__ == '__main__':
    size = 0
    max_space = False
    original_data = [8, 3, 15, 2, 9, 1, 5, 7, 4, 16, 10, 11, 12, 13, 6, 14]
    print("합병 정렬 전 데이터는 : ", original_data)
    merge_sort(len(original_data), original_data)
    print("합병 정렬 후 데이터는 : ", original_data)
    print("합병정렬 알고리즘 수행에 필요한 추가적인 공간의 크기는 : ", size)