Machine Learning - Singular Value Decomposition

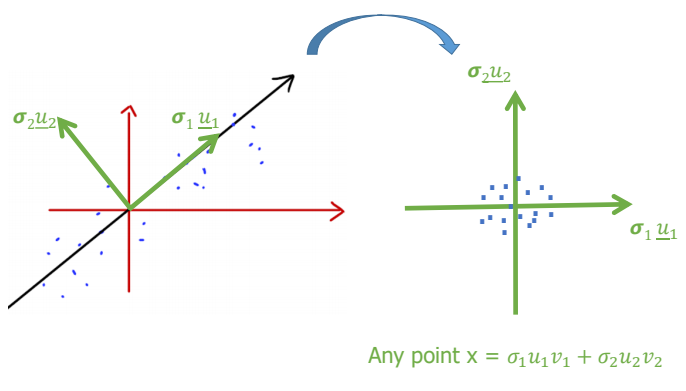
SVD 기초

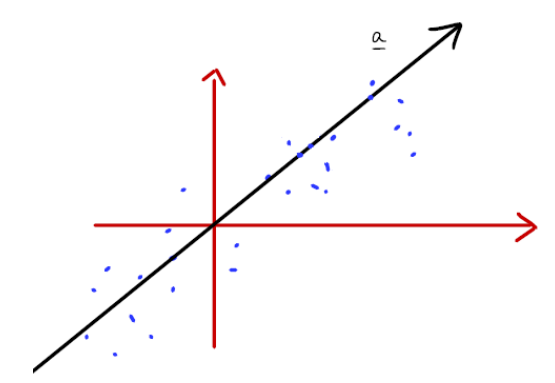
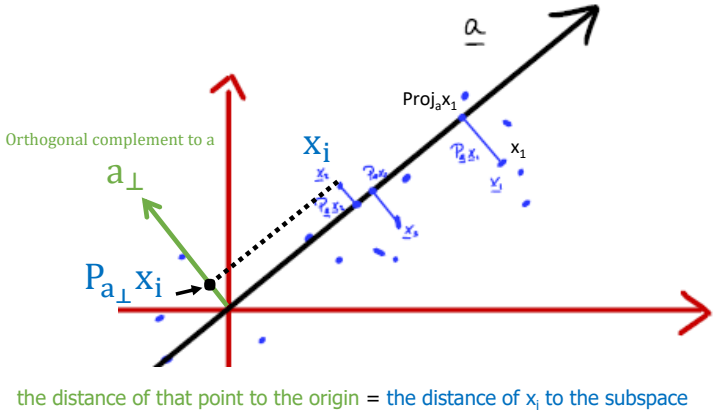
• 데이터를 잘 설명할 수 있는 a벡터를 구하고자 하는 것이 목적이다.
• 각 데이터와 a벡터 사이 간의 거리를 $d_i^2 = ||x_i - Proj_ax_i||^2_2$로 나타낼 수 있으며 Machine learning에서는 $\sum^p_{i=1}d^2_i$의 최소치를 구하는 것이 목적이다.

Projection Matrices

• 앞선 이론에서 projection matrices는 $Proj_AX = A(A^TA)^{-1}A^TX$로 표현할 수 있다.

Properties of projection matrices

• $P_A = P_A^2 = P_AP_A$
• $P_A = P_A^T = P_A^TP_A$
• A가 Single column vector일 때는 다음과 같이 표현된다.
  

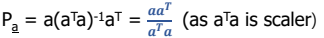
Orthogonal complete로의 표현

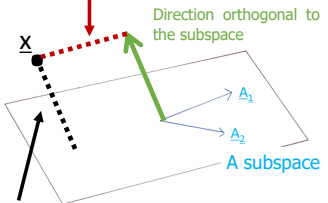
• A가 생성한 공간의 orthogonal complement의 기저를 B라고 한다면 $A^TB=0$이며 어떠한 벡터도 A와 B로 표현할 수 있다.
  

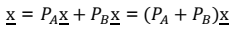
• 위의 식을 변형하면 Orthogonal complement에 대한 다음의 식을 얻을 수 있다.
  

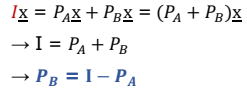
d의 식표현

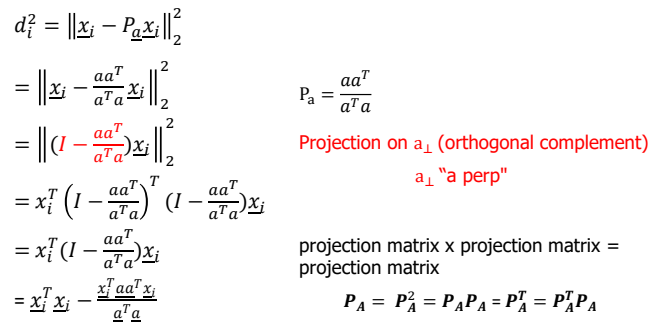
• d의 최소화된 거리를 구하기 위하여 $\hat a$의 최댓값을 구하며 1st left singular vector라고 정의한다.
  

SVD

• SVD에서는 식을 $X = U\Sigma V^T$로 표현한다.

U

• U는 Left singular vectors이다.
• orthogonal matrix이며 X의 Columns의 orthogonal basis이다.

V

• V는 Right singular vectors이다.
• orthogonal matrix이며 X의 각 Column을 나타내기 위하여 필요한 basis coefficients이다.

Sigma

• $\Sigma$는 양수를 요소로 가지는 diagonal matrix이다.
  

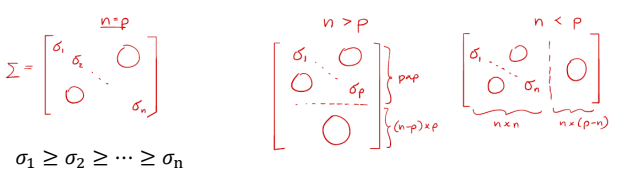
적용

• U = [$u_1, u_2, ..., u_n$]이라면 각 벡터는 X의 기저를 나타내면 다음과 같이 표현된다.
  

• $u_2$는 $u_1$의 orthogonal vector이며 데이터의 경향성과 orthogonal을 표현함으로써 데이터를 편하게 다루기 위한 rotate에 사용될 수 있다.
  

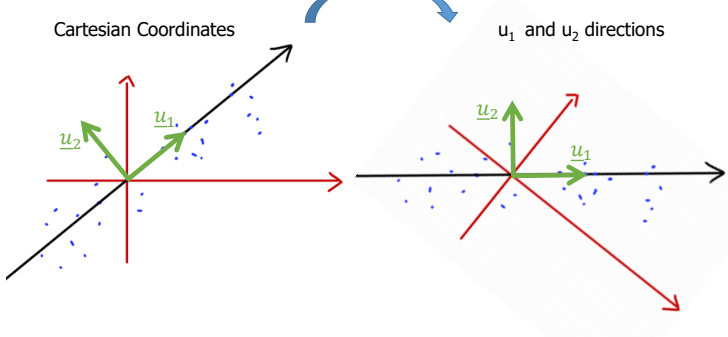
• $\Sigma$의 $\sigma_1,\sigma_2, ...$은 대각행렬로써 X의 각 열의 크기를 나타낸다.

• 따라서 $\sigma_1,\sigma_2, ...$는 데이터의 분포도를 나타내면 데이터의 Rescale에 사용된다.