Machine Learning - 이론 기초 part3

용어정리

Subspace

• 데이터를 나타내는 X행렬이 요소 벡터들이 생성할 수 있는 공간을 나타낸다.
• The hyperplane span(col(X)) X is called a subspace
  

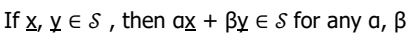
basis(기저)

• X의 Columns이 선형독립이라면 공간을 이루는 기저라고 지칭한다.

$\hat y$

• 예측된 값으로 데이터 X행렬과 가중치를 곱하여 도출된다.
  
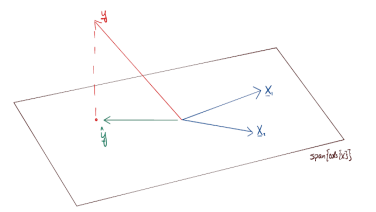
• True value y는 subspace상에 없으며 $\hat y$는 y의 subspace로의 projection된 값이다.

How to represent a subspace?

• 공간을 벡터들의 집합으로 나타낸다.
• 선형독립인 벡터들을 표시한다.
• 선택된 벡터들을 orthonormal(Orthogonal + Norm)으로 표현한다.
  • norm : length = 1

Properties of the orthonormal basis matrix

• U를 정규직교벡터라고 한다면 어떠한 벡터와 곱하여도 길이의 제곱갑을 보존할 수 있다.
  

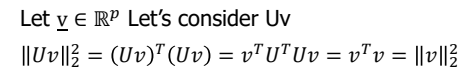
Subspace의 다른 표현

• 구하고자 하는 $\hat w = argmin_w||y-Xw||^2, \hat y = X\hat w$의 식을 세운다.
• 앞선 Least squars의 식에 따르면 $\hat w = (X^TX)^{-1}X^Ty$이며 projection matrix로 바꾸어 표현하면 $\hat y = X\hat w$에 대입함으로써 $\hat y = X(X^TX)^{-1}X^Ty=P_Xy$로 표현할 수 있다.

• subspace의 구성 벡터들을 정규직교 벡터로 표현할 수 있다.
  
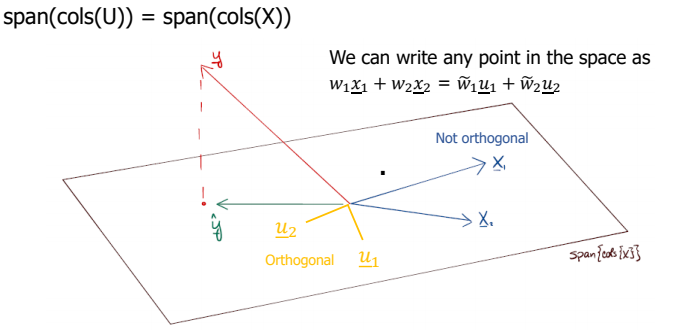
• 같은 값을 다른 식으로 표현할 수 있으며 계산이 정규직교벡터들로 바꿈으로써 이점을 얻을 수 있다.
• 따라서 $\hat y = X(X^TX)^{-1}X^Ty=P_Xy$식의 X를 U로 대체하면 $\hat y = U(U^TU)^{-1}U^Ty=P_Xy$로 표현되며
  
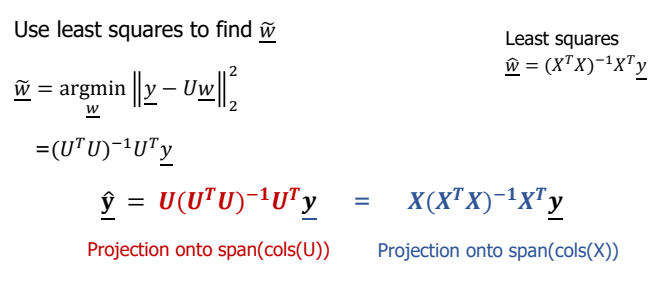
• 정규직교벡터의 성질에 의하여 다음과 같이 표현된다.
  
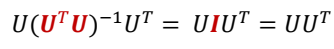
• 따라서 Subspace에 대한 projection식은 $\hat y=UU^Ty$로 표현되며 역행렬을 구할 필요 없이 subspace를 표현할 수 있다.