Machine Learning - 이론 기초

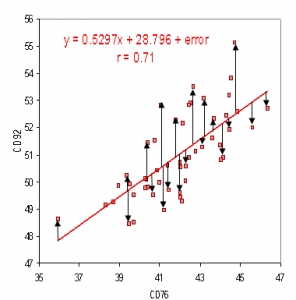
기본 용어

$X_{ij}$

• $j^{th}$ feature of $i^{th}$ Sample

벡터의 내적

• $a\bullet b = a^Tb = \sum_{K=I,D}a_kb_k$

$\hat y_i$

• 예측되는 값 i번째 값

벡터의 p차 Norm

• 벡터의 길이 혹은 크기를 측정하는 방법/함수
• Norm이 측정한 벡터의 크기는 원점에서 벡터 좌표까지의 거리 혹은 Magnitude라고 한다.
• $||X||_p = (\sum_{i = 1,d}|x_i|^p)^{1/p}$
• p는 Norm의 차수를 의미하며 p가 1이면 1차 Norm, 2이면 2차 Norm이라고 한다.
• 주로 사용되는 Norm은 1차 Norm, 2차 Norm, Maxium Norm이다.

L1 Norm

• 1차놈이며 Tacxicab Norm, Manhattan Norm이라고도 한다.
• 벡터의 요소에 대한 절댓값의 합이며 요소의 값 변화를 정확하게 파악할 수 있다.

L2 Norm

• 2차놈이며 n차원 좌표평면(유클리드 공간)에서 벡터의 크기를 계산하기 때문에 Euclidean Norm이라고도 한다.

벡터의 표현

X = $\begin{bmatrix}1&x_1&x_1^2&x_1^3\\2&x_2&x_2^2&x_2^3\\..&..&..&..\\1&x_n&x_n^2&x_n^3 \end{bmatrix}$ 이라고 하면

$\hat y = Xw$와 같이 선형으로 나타내거나 $\hat y_i$ = $w_1$ + $w_2x_i$ + $w_3x_i^3$ + $w_4x_i^3$와 같이 비선형/ Cubic polynomial 형태로 나타낼 수 있다.

• $\hat y_i = w_0 + w_1x_1 + .. + w_px_{ip}$로 표현할 수 있으며 $w_0$은 offset을 지칭한다.
• W는 가중치 행렬을 의미하며 위의 식은 $<W, x_i> or <x_i, W>$로 표현될 수 있다.

Residual

• 잔차이며 결과의 오류 값이다.
• Residual $r_i$는 True value를 y라고 할 때 $y-\hat y_i$ or $r_i(w) = y_i - \hat y_i(w)$로 표현된다.

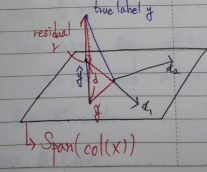
• Span은 구성 벡터들로 형성할 수 있는 공간을 의미한다.
• $\hat y$는 벡터 $x_1,x_2$가 span한 공간에서 y와 가장 가까운 점에 projection한 점을 뜻한다.

Machine Learning의 목적

• 잔차의 최소화
• $\hat w = argmin_w ||r(w)||^2$
• 2번째 그림과 같이 $||\hat r|| = ||r||^2 + ||d||^2$로 표현할 수 있으며 좌표 공간의 거리를 구하기 위하여 2차 Norm을 사용한다.
• d가 최소화될 수록 잔차 r도 감소하며 따라서 유클리드 거리 중 최소거리를 찾는 과정

Least Squares Estimations

• Euclidean Norm을 이용하여 거리를 구하고 제곱의 값으로 잔차를 판별한다.

제곱 사용의 이점

• 양수와 음수 모두 같은 결과로써 사용할 수 있다.
• 수학적으로 계산이 쉬워진다.
• 큰 error일수록 그 차이를 증가시킨다.
• 기하학적으로 표현하기 쉬워진다.
• Gaussizn noise model과 양립가능하다.

$\hat w$ 식 도출

적용 이론

선형독립

• 벡터 $v_1, v_2, ..., v_n$이 있을 때 모든 계수가 0인 경우를 제외하고 어떤 선형조합으로도 0을 만들 수 없다면 독립

Rank

• 행렬의 열들 중 선형독립인 열들의 최대 개수
• 행과 열의 Rank는 항상 독립적이다.
• $rank(A) = rank(A^TA) = rank(AA^T)$

Full Rank

• 한 열이나 행에서 전부 다 선형독립인 벡터기저들을 가진 경우
• rank(X) = min(n, p)

inverse

• 행렬이 full rank일 때만 역행력을 가진다.
• $X \in R^{n * p}$ assume that n >= p, rank(X) = p
• X가 Full rank라면 역행렬의 가짐을 의미한다.

식 도출

• ML은 $\hat w = argmin_w ||r(w)||^2$의 값을 구하기 위해 실행된다.
• $\hat r = y - \hat y$로 표현되기에 $y - X\hat w$로 표현될 수 있으며 양변에 $X^T$를 곱해주면 $X^T\hat r = X^T(y-X\hat w)$ 로 식이 정리된다.
• $X^T\hat r = X^T(y-X\hat w)$에서 2번째 그림과 같이 X와 r은 orthogonal이므로 0의 값을 가진다. 따라서 $X^T\hat r = X^T(y-X\hat w) = 0$
• 식을 정리하면 $X^Ty = X^TX\hat w$
• 적용 이론에서 X가 Full rank를 가진다고 가정하면 양변에 역행렬을 취함으로써 $\hat w = (X^TX)^{-1}X^Ty$의 식이 도출된다.

$\hat w = (X^TX)^{-1}X^Ty$