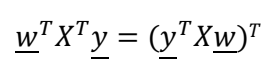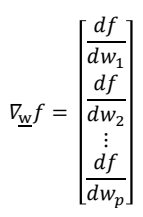Classification
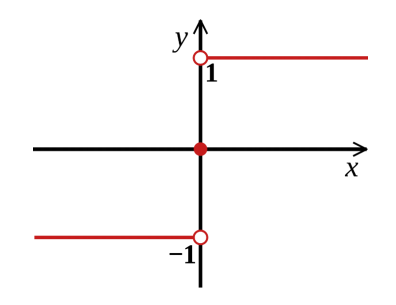
- True value인 y가 {-1, 1}을 가지는 이진 분류라고 가정한다.
- 를 계산하는 것이 machine learning의 목적이며 sum of squares값을 최소화되도록 한다.
- 따라서 Treu value인 y와 predicted value인 Xw()간의 거리를 최소화 한다.
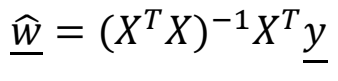
- 따라서 Treu value인 y와 predicted value인 Xw()간의 거리를 최소화 한다.
Classification Rule
- 예측되는 값은 확률적으로 혹은 -1 or 1 값이 아닌 0.5, -0.7과 같은 값을 가질 수 있다.
- 이진분류의 경우에는 sign func와 같은 classification rule을 바탕으로 Machine learning의 목적을 달성할 수 있다.
- sign func
Optimization approach
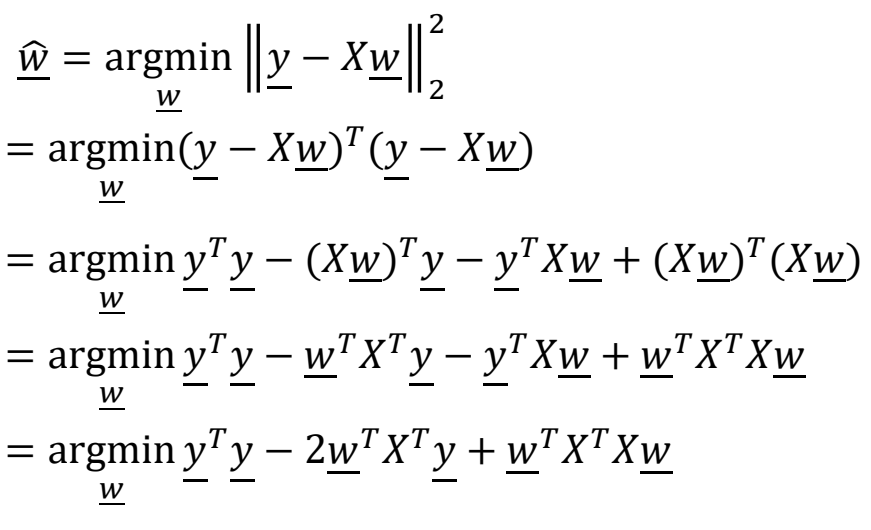
Positive definite matrix(양의 정부호 행렬)
- 0이 아닌 모든 벡터 X에 대하여
- 인 행렬에 대하여 이 존재한다는 것은 가 양의 정부호행렬임을 의미한다.
Properties of Positive Definite Matrices
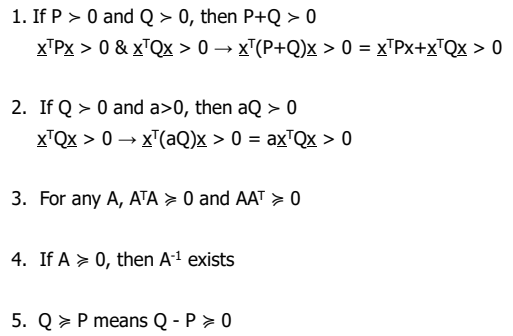
Convexity
- Convex
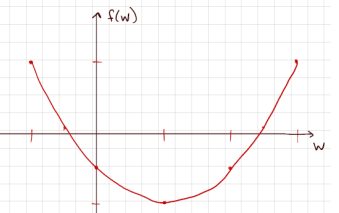
함수 위의 두 점을 연결하는 선을 그었을 때 함수 그래프 위만을 지나간다면 convex하다고 한다.
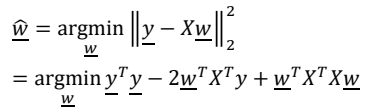
- 위의 식에서 는 y의 2차함수 형태로 나타낼 수 있으며 Positive definite의 3번 성질로 인해 최고차항의 계수가 양수이다.
- 따라서 Convex의 성질을 가지며 미분을 통하여 최솟값을 구할 수 있다.
미분을 통한 최적의 식 도출
- 벡터의 미분은 다음과 같이 표현된다.
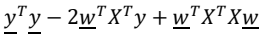 의 식을 미분한 후 최솟값을 구하기 위하여 우변을 0으로 설정하면
의 식을 미분한 후 최솟값을 구하기 위하여 우변을 0으로 설정하면 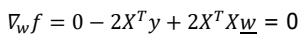 의 식을 얻을 수 있으며 이항하여 정리를 통하여
의 식을 얻을 수 있으며 이항하여 정리를 통하여 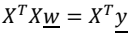
식을 얻을 수 있다. 가 Positive definite이기 때문에 역행렬을 취한다면
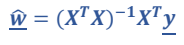
의 최적화된 식을 얻을 수 있다.