from sklearn.datasets import load_digits
import matplotlib.pyplot as plt
import numpy as np
digits = load_digits()1.1. After loading the dataset, visualize the first few digits datasets
fig = plt.figure(figsize=(4, 4))
for i in range(64):
ax = fig.add_subplot(8, 8, i + 1, xticks=[], yticks=[])
ax.set_axis_off()
ax.imshow(digits.images[i], cmap=plt.cm.binary, interpolation='nearest') 
1.2. Classify the digits using random forest.
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
n_samples = len(digits.images)
data = digits.images.reshape((n_samples, -1))
clf = RandomForestClassifier( random_state=123)
X_train, X_test, y_train, y_test = train_test_split(
data, digits.target, test_size=0.2, shuffle=False)
from sklearn.model_selection import GridSearchCV, RepeatedKFold
param_grid = {'max_depth' : np.arange(10,20,1)}
grid = GridSearchCV(clf, param_grid = param_grid,
cv=RepeatedKFold(n_splits=5, n_repeats=5, random_state = 123),
return_train_score=True)
grid.fit(X_train, y_train)
print(f"best parameters: {grid.best_params_}")
print(f"valid-set score: {grid.score(X_test, y_test):.3f}")best parameters: {'max_depth': 14}
valid-set score: 0.931
1.3. show the classification report and discuss the results.
y = clf.predict(data)
fig = plt.figure(figsize=(13, 13))
for i in range(64):
ax = fig.add_subplot(8, 8, i + 1, xticks=[], yticks=[])
ax.set_axis_off()
ax.imshow(digits.images[i], cmap=plt.cm.binary, interpolation='nearest')
ax.set_title(f'Prediction: {y[i]}')
for i in range(10,20):
clf = RandomForestClassifier(max_depth = i, random_state=123)
clf.fit(X_train, y_train)
predicted = clf.predict(X_test)
print("max_depth =",i, " Error : ", (predicted != y_test).sum(),
" accuracy : ",(len(y_test) - (predicted != y_test).sum()) / len(y_test))예측이 잘못된 경우 시각화
fig = plt.figure(figsize=(15, 5))
i = 1
for j in np.where(predicted != y_test)[0]:
p = X_test[j].reshape(8,8)
ax = fig.add_subplot(3, 9, i)
ax.set_axis_off()
ax.imshow(p, cmap=plt.cm.binary, interpolation='nearest')
ax.set_title(f'Prediction: {predicted[j]}')
i += 1 1.4. Plot confusion matrix and discuss the results.
from sklearn.metrics import confusion_matrix, plot_confusion_matrix
from sklearn.metrics import classification_report
fig, ax = plt.subplots(figsize=(9, 9))
clf = RandomForestClassifier(max_depth = 14, random_state=123).fit(X_train,y_train)
plot_confusion_matrix(clf, X_test, y_test, cmap='gray_r', ax=ax)
1.5. Apply PCA to the digits dataset to project them to 2 dimensions and visualize the first twocomponents (2d scatter plot). Discuss the results.
from sklearn.decomposition import PCA
print(data.shape)
pca = PCA(n_components=2)
X_pca = pca.fit_transform(data)
plt.scatter(X_pca[:, 0], X_pca[:, 1])
print(X_pca.shape)
plt.xlabel("first principal component")
plt.ylabel("second principal component")
1.6. A vital part of using PCA in practice is the ability to estimate how many components are needed to describe the data. This can be determined by looking at the cumulative explained variance ratio as a function of the number of components. Plot the "cumulative explained variance ratio (y-axis)” as a function of “number of component” (x-axis).
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import scale, StandardScaler
pca_scaled = make_pipeline(StandardScaler(), PCA())
pca_scaled.fit(X_train, y_train)
pca = pca_scaled.named_steps['pca']
fig, axes = plt.subplots(2)
axes[0].plot(pca.explained_variance_ratio_)
axes[1].semilogy(pca.explained_variance_ratio_)
for ax in axes:
ax.set_xlabel("component index")
ax.set_ylabel("explained variance ratio")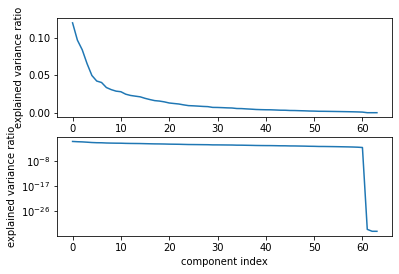
1.7. You will apply k-means on the same simple digits data to try to identify similar digits without using the original label information; this might be similar to a first step in extracting meaning from a new dataset about which you don’t have any a prior label information. Apply k-means clustering to the digits dataset with 10 clusters. The result will be 10 clusters and 64 dimensions. Notice that the cluster centers themselves are 64- dimenstional points, and themselves be interpreted as the “typical” digit within the cluster. Visualize what these cluster centers look like (plot 10 different digits images like below). Hint: reshape kmeans.clustercenters to create the digits images. And discuss the results.
from sklearn.cluster import KMeans
data = scale(digits.data)
kmeans = KMeans(n_clusters=10, random_state=123)
kmeans.fit(data)
print(kmeans.cluster_centers_.shape)
def print_digits(images,y,max_n=10):
fig = plt.figure(figsize=(12,12))
fig.subplots_adjust(left=0,right=1,bottom=0,top=1,hspace=0.05,wspace=0.05)
i=0
while i<max_n and i<images.shape[0]:
p=fig.add_subplot(20,20,i+1,xticks=[],yticks=[])
p.imshow(images[i],cmap=plt.cm.bone)
p.text(0,14,str(y[i]))
i = i + 1
print_digits(digits.images, digits.target,max_n=10)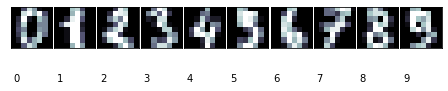
kmeans = KMeans(n_clusters=10, random_state=0)
clusters = kmeans.fit_predict(digits.data)
print(kmeans.cluster_centers_.shape)
fig, ax = plt.subplots(2, 5, figsize=(4, 3))
centers = kmeans.cluster_centers_.reshape(10, 8, 8)
for axi, center in zip(ax.flat, centers):
axi.set_axis_off()
axi.set(xticks=[], yticks=[])
axi.imshow(center, interpolation='nearest', cmap=plt.cm.binary)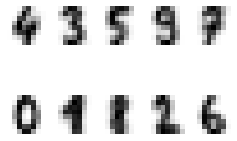
1.8. Because k-means knows nothing about the identity (label) of the cluster, the 0-9 labels may be permuted. Fix this by matching each learned cluster label with the true labels and check how accurate our unsupervised clustering is in finding similar digits within the data. Hint: accuracy_score
from scipy.stats import mode
labels = np.zeros_like(clusters)
for i in range(10):
mask = (clusters == i)
labels[mask] = mode(digits.target[mask])[0]
from sklearn.metrics import accuracy_score
accuracy_score(digits.target, labels)
X_train, X_test,y_train,y_test,images_train,images_test = train_test_split(data, digits.target, digits.images, test_size=0.2,random_state=123)
n_samples,n_features = X_train.shape
n_digits = len(np.unique(y_train))
labels2 = y_train
from sklearn.metrics import accuracy_score
from sklearn import cluster
clf = cluster.KMeans(init='k-means++',n_clusters=10,random_state=123)
clf.fit(X_train)
y_pred=clf.predict(X_test)
accuracy_score(y_test, y_pred)
def print_cluster(images,y_pred,cluster_number):
images = images[y_pred==cluster_number]
y_pred=y_pred[y_pred==cluster_number]
print_digits(images,y_pred,max_n=10)
for i in range(10):
print_cluster(images_test,y_pred,i)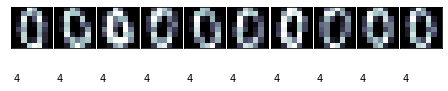
print("Data size : ",len(y_pred))
print('Error :', (y_pred != y_test).sum())Data size : 360
Error : 288
1.9. With just a simple k-means algorithm, we can discover the correct groups for [your accuracy score in 1.8] of the input digits. Plot the confusion matrix and check for this and discuss the results.
import seaborn as sns
mat = confusion_matrix(digits.target, labels)
sns.heatmap(mat.T, square=True, annot=True, fmt='d', cbar=False,
xticklabels=digits.target_names,
yticklabels=digits.target_names)
plt.xlabel('true label')
plt.ylabel('predicted label')
