import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
import pandas as pd
import sklearn
- Determine which features are continuous and which are categorical.
credit = pd.read_csv("credit-g.csv")
categorical = credit.dtypes == object
continuous = credit.loc[:, ~categorical]
contype = credit.dtypes == credit[continuous.columns[0]].dtypes
categorical = credit.loc[:, ~contype]
categorical = categorical.drop(categorical.columns[13], axis = 1)
- Visualize the univariate distribution of each continuous feature, and the distribution of the target.
i = 0
for i in range(0,len(continuous.columns)):
continuous[continuous.columns[i]].hist(bins = 'auto')
plt.xlabel(continuous.columns[i])
plt.show()
i += 1
- Split data into training (70%), validation (10%), and test set (20%). Do not use the test set until a final evaluation in 5. Preprocess the data without using a pipeline and evaluate an initial Logistic Regression model with the training and validation split.
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split, cross_val_score
from sklearn.preprocessing import StandardScaler, LabelEncoder, OneHotEncoder
mapping = { 'good' : 1, 'bad' : -1}
credit['class'] = credit['class'].map(mapping)
X = credit.drop('class', axis = 1)
y = credit['class'].values
le = LabelEncoder()
k = 0
for k in range(len(categorical.columns)):
X[categorical.columns[k]] = le.fit_transform(X[categorical.columns[k]])
k += 1
X_temp, X_test, y_temp, y_test = \
train_test_split(X, y, test_size=0.2,
shuffle=True, random_state=123, stratify=y)
X_train, X_valid, y_train, y_valid = \
train_test_split(X_temp, y_temp, test_size=0.125,
shuffle=True, random_state=123, stratify=y_temp)
std = StandardScaler()
logreg = LogisticRegression(C = 1, max_iter=10000)
X_train_std = std.fit_transform(X_train)
X_valid_std = std.fit_transform(X_valid)
acc = logreg.fit(X_train_std, y_train)
print("train-set accuracy : ", acc.score(X_train_std,y_train))
print("valid-set accuracy : ", acc.score(X_valid_std,y_valid))
- Use ColumnTransformer and pipeline to encode categorical variables (your choice of OneHotEncoder or another one from the categorical_encoder package, or both). Evaluate Logistic Regression, Linear Support Vector Machines and Random Forests using cross-validation. How different are the results? How does scaling the continuous features with StandardScaler influence the results?
from sklearn.impute import SimpleImputer
from sklearn.compose import make_column_transformer, make_column_selector
from sklearn.pipeline import make_pipeline
from sklearn.svm import SVC
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
cat_preprocessing = make_pipeline(SimpleImputer(strategy='constant', fill_value='NA'),
OneHotEncoder(handle_unknown='ignore'))
cont_preprocessing = make_pipeline(SimpleImputer(), StandardScaler())
preprocess = make_column_transformer((cat_preprocessing, make_column_selector(dtype_include='object')),
remainder=cont_preprocessing)
credit1 = pd.read_csv("credit-g.csv")
X1 = credit1.drop('class', axis = 1)
y1 = credit1['class'].values
X1_temp, X1_test, y1_temp, y1_test = \
train_test_split(X1, y1, test_size=0.2,
shuffle=True, random_state=123, stratify=y)
X1_train, X1_valid, y1_train, y1_valid = \
train_test_split(X1_temp, y1_temp, test_size=0.125,
shuffle=True, random_state=123, stratify=y_temp)
print("LogisticRegression accuracy, train_set :\n",cross_val_score(make_pipeline(preprocess, LogisticRegression(C = 1, max_iter=10000)), X1_train, y1_train, cv=5))
print("LogisticRegression accuracy, valid_set :\n",cross_val_score(make_pipeline(preprocess, LogisticRegression(C = 1, max_iter=10000)), X1_valid, y1_valid, cv=5))
print("Linear Support Vector Machines accuracy, train_set :\n",cross_val_score(make_pipeline(preprocess, SVC(kernel = 'linear')), X1_train, y1_train, cv=5))
print("Linear Support Vector Machines accuracy, valid_set :\n",cross_val_score(make_pipeline(preprocess, SVC(kernel = 'linear')), X1_valid, y1_valid, cv=5))
print("Random Forests accuracy, train_set :\n",cross_val_score(make_pipeline(preprocess, RandomForestClassifier(random_state=0)), X1_train, y1_train, cv=5))
print("Random Forests accuracy, valid_set :\n",cross_val_score(make_pipeline(preprocess, RandomForestClassifier(random_state=0)), X1_valid, y1_valid, cv=5))
cat_preprocessing = make_pipeline(SimpleImputer(strategy='constant', fill_value='NA'),
OneHotEncoder(handle_unknown='ignore'))
cont_preprocessing = make_pipeline(SimpleImputer())
preprocess = make_column_transformer((cat_preprocessing, make_column_selector(dtype_include='object')),
remainder=cont_preprocessing)
print("LogisticRegression accuracy, train_set :\n",cross_val_score(make_pipeline(preprocess, LogisticRegression(C = 1, max_iter=10000)), X1_train, y1_train, cv=5))
print("LogisticRegression accuracy, valid_set :\n",cross_val_score(make_pipeline(preprocess, LogisticRegression(C = 1, max_iter=10000)), X1_valid, y1_valid, cv=5))
print("Linear Support Vector Machines accuracy, train_set :\n",cross_val_score(make_pipeline(preprocess, SVC(kernel = 'linear')), X1_train, y1_train, cv=5))
print("Linear Support Vector Machines accuracy, valid_set :\n",cross_val_score(make_pipeline(preprocess, SVC(kernel = 'linear')), X1_valid, y1_valid, cv=5))
print("Random Forests accuracy, train_set :\n",cross_val_score(make_pipeline(preprocess, RandomForestClassifier(random_state=0)), X1_train, y1_train, cv=5))
print("Random Forests accuracy, valid_set :\n",cross_val_score(make_pipeline(preprocess, RandomForestClassifier(random_state=0)), X1_valid, y1_valid, cv=5))
- Tune the parameters using GridSearchCV. Do the results improve? Evaluate only the be model on the test set. And visualize the performance as function of the parameters for all three models.
from sklearn.model_selection import GridSearchCV, RepeatedKFold, RepeatedStratifiedKFold
classifier = SVC(kernel = 'linear')
logreg = LogisticRegression(C = 1, max_iter=10000)
rfc = RandomForestClassifier(random_state=0)
c_values = np.arange(0.1,10,0.1)
param_grid = dict(C=c_values)
grid = GridSearchCV(logreg, param_grid = param_grid,
cv = RepeatedStratifiedKFold(n_splits=5, n_repeats=3), return_train_score=True)
grid.fit(X_train,y_train)
print(f"best parameters: {grid.best_params_}")
print(f"test-set score: {grid.score(X_test, y_test):.3f}")
results = pd.DataFrame(grid.cv_results_)
results.plot('param_C', 'mean_train_score')
results.plot('param_C', 'mean_test_score', ax=plt.gca())
plt.fill_between(results.param_C.astype(np.float64),
results['mean_train_score'] + results['std_train_score'],
results['mean_train_score'] - results['std_train_score'], alpha=0.2)
plt.fill_between(results.param_C.astype(np.float64),
results['mean_test_score'] + results['std_test_score'],
results['mean_test_score'] - results['std_test_score'], alpha=0.2)
plt.legend()
a_train = std.fit_transform(X_train)
a_test = std.fit_transform(X_test)
param_grid2 = { 'C': np.arange(0.1,50,0.5), 'gamma': [0.1]}
grid2 = GridSearchCV(classifier, param_grid = param_grid2,
cv = RepeatedStratifiedKFold(n_splits=3, n_repeats=3), return_train_score=True)
grid2.fit(a_train,y_train)
print(f"best parameters: {grid2.best_params_}")
print(f"test-set score: {grid2.score(a_test, y_test):.3f}")
results2 = pd.DataFrame(grid2.cv_results_)
results2.plot('param_C','mean_train_score')
results2.plot('param_C','mean_test_score', ax=plt.gca())
plt.fill_between(results2.param_C.astype(np.float64),
results2['mean_train_score'] + results2['std_train_score'],
results2['mean_train_score'] - results2['std_train_score'], alpha=0.2)
plt.fill_between(results2.param_C.astype(np.float64),
results2['mean_test_score'] + results2['std_test_score'],
results2['mean_test_score'] - results2['std_test_score'], alpha=0.2)
plt.legend()
max_depth = np.arange(1,20,1)
param_grid3 = {'max_depth': max_depth }
grid3 = GridSearchCV(rfc, param_grid = param_grid3,
cv = RepeatedStratifiedKFold(n_splits=5, n_repeats=3), return_train_score=True)
grid3.fit(a_train,y_train)
print(f"best parameters: {grid3.best_params_}")
print(f"test-set score: {grid3.score(a_test, y_test):.3f}")
results3 = pd.DataFrame(grid3.cv_results_)
results3.plot('param_max_depth', 'mean_train_score')
results3.plot('param_max_depth', 'mean_test_score', ax=plt.gca())
plt.fill_between(results3.param_max_depth.astype(np.float64),
results3['mean_train_score'] + results3['std_train_score'],
results3['mean_train_score'] - results3['std_train_score'], alpha=0.2)
plt.fill_between(results3.param_max_depth.astype(np.float64),
results3['mean_test_score'] + results3['std_test_score'],
results3['mean_test_score'] - results3['std_test_score'], alpha=0.2)
plt.legend()
param_grid3 = {'n_estimators' : np.arange(1,100,5) }
grid3 = GridSearchCV(rfc, param_grid = param_grid3,
cv = RepeatedStratifiedKFold(n_splits=5, n_repeats=3), return_train_score=True)
grid3.fit(a_train,y_train)
print(f"best parameters: {grid3.best_params_}")
print(f"test-set score: {grid3.score(a_test, y_test):.3f}")
results3 = pd.DataFrame(grid3.cv_results_)
results3.plot('param_n_estimators', 'mean_train_score')
results3.plot('param_n_estimators', 'mean_test_score', ax=plt.gca())
plt.fill_between(results3.param_n_estimators.astype(np.float64),
results3['mean_train_score'] + results3['std_train_score'],
results3['mean_train_score'] - results3['std_train_score'], alpha=0.2)
plt.fill_between(results3.param_n_estimators.astype(np.float64),
results3['mean_test_score'] + results3['std_test_score'],
results3['mean_test_score'] - results3['std_test_score'], alpha=0.2)
plt.legend()
- Change the cross-validation strategy from ‘stratified k-fold’ to ‘kfold’ with shuffling. Do the parameters that are found change? Do they change if you change the random seed of the shuffling? Or if you change the random state of the split into training and test data?
X2_temp, X2_test, y2_temp, y2_test = \
train_test_split(X, y, test_size=0.2,
shuffle=True, random_state=123)
X2_train, X2_valid, y2_train, y2_valid = \
train_test_split(X2_temp, y2_temp, test_size=0.125,
shuffle=True, random_state=123)
results = pd.DataFrame(grid.cv_results_)
results.plot('param_C', 'mean_train_score')
results.plot('param_C', 'mean_test_score', ax=plt.gca())
plt.fill_between(results.param_C.astype(np.float64),
results['mean_train_score'] + results['std_train_score'],
results['mean_train_score'] - results['std_train_score'], alpha=0.2)
plt.fill_between(results.param_C.astype(np.float64),
results['mean_test_score'] + results['std_test_score'],
results['mean_test_score'] - results['std_test_score'], alpha=0.2)
plt.legend()
X2_temp, X2_test, y2_temp, y2_test = \
train_test_split(X, y, test_size=0.2,
shuffle=True, random_state=100)
X2_train, X2_valid, y2_train, y2_valid = \
train_test_split(X2_temp, y2_temp, test_size=0.125,
shuffle=True, random_state=100)
c_values = np.arange(0.1,10,0.1)
param_grid = dict(C=c_values)
grid = GridSearchCV(logreg, param_grid = param_grid,
cv = RepeatedKFold(n_splits=5, n_repeats=3), return_train_score=True)
grid.fit(X2_train,y2_train)
print(f"best parameters: {grid.best_params_}")
print(f"test-set score: {grid.score(X2_test, y2_test):.3f}")
results = pd.DataFrame(grid.cv_results_)
results.plot('param_C', 'mean_train_score')
results.plot('param_C', 'mean_test_score', ax=plt.gca())
plt.fill_between(results.param_C.astype(np.float64),
results['mean_train_score'] + results['std_train_score'],
results['mean_train_score'] - results['std_train_score'], alpha=0.2)
plt.fill_between(results.param_C.astype(np.float64),
results['mean_test_score'] + results['std_test_score'],
results['mean_test_score'] - results['std_test_score'], alpha=0.2)
plt.legend()
- Visualize the 20 most important coefficients for Logistic Regression and Linear Support Vector Machines using hyper-parameters that performed well in the grid-search.
classifier = SVC(kernel = 'linear', C = 0.1, gamma = 0.1)
logreg = LogisticRegression(C = 0.1, max_iter=10000)
coef = logreg.fit(X_train,y_train)
coef2 = classifier.fit(X_train,y_train)
print(coef.coef_, coef.intercept_)
print(coef2.coef_, coef2.intercept_)
df = pd.DataFrame(coef.coef_)
plt.scatter(df.columns,df.values)
df2 = pd.DataFrame(coef2.coef_)
plt.scatter(df2.columns,df2.values)
- Using optimized models that performed well in the grid-search, compute the performance of all three models using confusion matrix, precision, recall, and F1-score. How different are the results? Also, calculate the true positive rate and false positive rate for all three models. Discuss the results.
from sklearn.metrics import confusion_matrix, plot_confusion_matrix
from sklearn.metrics import classification_report
lr = LogisticRegression(C =0.1, max_iter=10000).fit(X_train, y_train)
y_pred = lr.predict(X_test)
print(confusion_matrix(y_test, y_pred))
print(classification_report(y_test, y_pred, target_names=['bad', 'good']))
print(f'TPR : {confusion_matrix(y_test, y_pred)[1][1]/confusion_matrix(y_test, y_pred)[1].sum():.3f}')
print(f'FPR : {confusion_matrix(y_test, y_pred)[0][1]/confusion_matrix(y_test, y_pred)[0].sum():.3f}')
fig, ax = plt.subplots(figsize=(2, 2))
plot_confusion_matrix(lr, X_test, y_test, cmap='gray_r', ax=ax)
svm = SVC(kernel = 'linear',C = 0.1, gamma = 0.1).fit(X_train, y_train)
y_pred2 = svm.predict(X_test)
print(confusion_matrix(y_test, y_pred2))
print(classification_report(y_test, y_pred2, target_names=['bad', 'good']))
print(f'TPR : {confusion_matrix(y_test, y_pred2)[1][1]/confusion_matrix(y_test, y_pred2)[1].sum():.3f}')
print(f'FPR : {confusion_matrix(y_test, y_pred2)[0][1]/confusion_matrix(y_test, y_pred2)[0].sum():.3f}')
fig, ax = plt.subplots(figsize=(2, 2))
plot_confusion_matrix(svm, X_test, y_test, cmap='gray_r', ax=ax)
rf = RandomForestClassifier(max_depth = 16).fit(X_train, y_train)
y_pred3 = rf.predict(X_test)
print(confusion_matrix(y_test, y_pred3))
print(classification_report(y_test, y_pred3, target_names=['bad', 'good']))
print(f'TPR : {confusion_matrix(y_test, y_pred3)[1][1]/confusion_matrix(y_test, y_pred3)[1].sum():.3f}')
print(f'FPR : {confusion_matrix(y_test, y_pred3)[0][1]/confusion_matrix(y_test, y_pred3)[0].sum():.3f}')
fig, ax = plt.subplots(figsize=(2, 2))
plot_confusion_matrix(rf, X_test, y_test, cmap='gray_r', ax=ax)
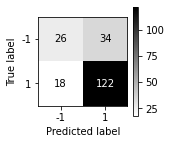
- Plot precision-recall (PR) curve and receiver operating characteristics (ROC) curve for all three models. Also, compute the performance of all three models using average precision and area under the curve (AUC). Discuss the results.
from sklearn.metrics import plot_precision_recall_curve, auc, plot_roc_curve
plot_precision_recall_curve(lr, X_test, y_test, name = 'Logistic')
plot_precision_recall_curve(svm, X_test, y_test, name = 'SVC')
plot_precision_recall_curve(rf, X_test, y_test, name = 'RandomForest')
plot_roc_curve(lr, X_test, y_test, name='Logistic')
plot_roc_curve(svm, X_test, y_test, name='SVC')
plot_roc_curve(rf, X_test, y_test, name = 'RandomForest')
from sklearn.metrics import average_precision_score
ap_lr = average_precision_score(y_test, lr.decision_function(X_test))
ap_svc = average_precision_score(y_test, svm.decision_function(X_test))
ap_rf = average_precision_score(y_test, rf.predict_proba(X_test)[:, 1])
print("Average precision of Logistic: {:.3f}".format(ap_svc))
print("Average precision of SVC: {:.3f}".format(ap_svc))
print("Average precision of RandomForest: {:.3f}".format(ap_rf))
from sklearn import metrics
lr_auc = metrics.roc_auc_score(y_test, lr.decision_function(X_test))
print("AUC of Logistic: {:.3f}".format(lr_auc))
svc_auc = metrics.roc_auc_score(y_test, svm.decision_function(X_test))
print("AUC of SVC: {:.3f}".format(svc_auc))
rf_auc = metrics.roc_auc_score(y_test, rf.predict_proba(X_test)[:, 1])
print("AUC of RandomForest: {:.3f}".format(rf_auc))

