[Paper Review] GAN : Generative Adversarial Nets

Paper link : https://arxiv.org/pdf/1406.2661.pdf

1. Introduction

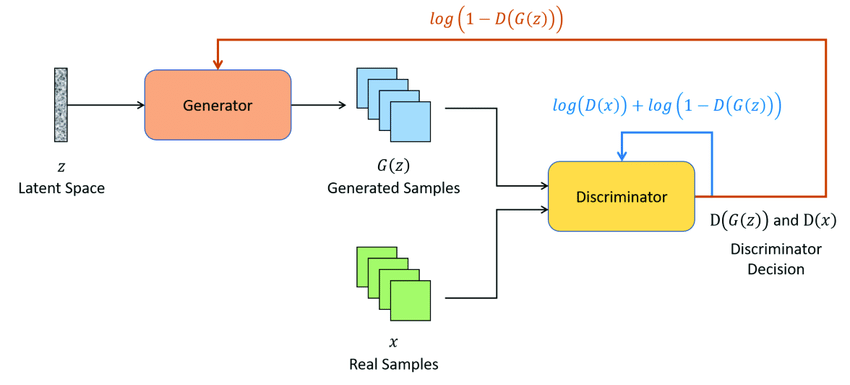
• GAN모델은 Generator(G, 생성기)와 Discriminator(D, 판별기)의 2개의 네트워크가 적대적으로 학습하며 이미지를 생성합니다.
• 논문에서 Generator와 Discriminator의 관계를 지폐위조범과 경찰의 관계에 비유합니다. 경찰(Discriminator)는 실제 지폐와 위조 지폐를 잘 구분할 수 있도록 학습되며, 지폐 위조범(Generator)은 경찰(Discriminator)이 생성된 위조 지폐를 실제 지폐라고 판단할 수 있도록 정교하고 사실적으로 만들도록 학습을 진행합니다.

  

2. 다변수 확률 분포

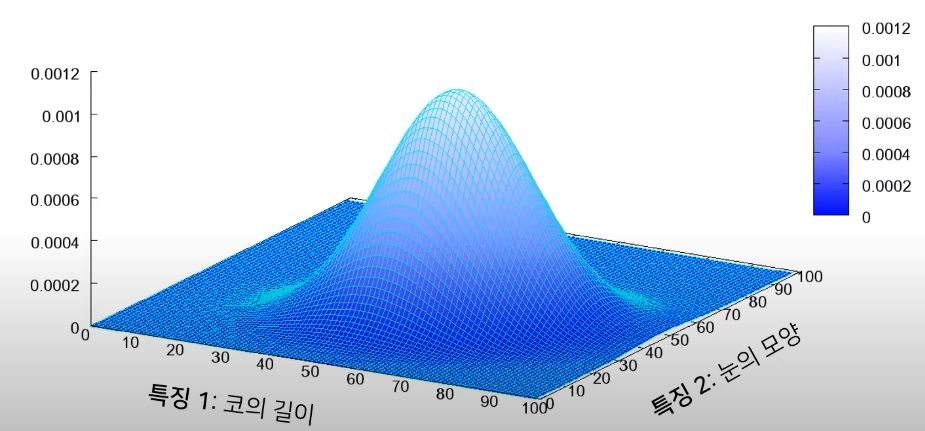
• image, audio, text 등의 데이터는 데이터 내의 feature를 기저로 삼은 고차원 공간 내에서 한 점으로 표현될 수 있습니다.

  

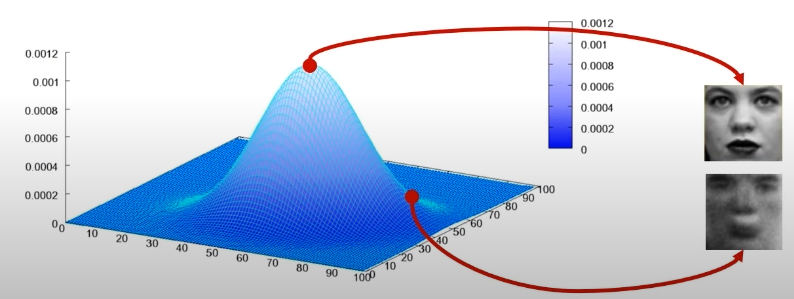
• 고차원 공간에서 한 점으로 표현된 데이터를 근사한 모델은 평균이나 분산과 같은 통계값을 가지게 되며, GAN 모델은 각각의 Class에 대한 데이터의 분포를 학습합니다.

  

• 데이터의 통계치를 가장 잘 반영한 분포를 학습한다면 더 좋은 데이터를 생성할 수 있게 되며, GAN Model은 확률이 높은 부분에서 noise를 삽입하며 사실적인 데이터를 생성할 수 있도록 학습이 진행됩니다.

3. GAN Model

3.1. Objective function

• GAN 모델의 목적함수는 다음과 같습니다.

  

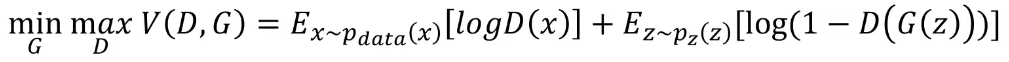
• 목적함수 V(D,G)는 판별기(D) 관점에서 높은 값을 가질 수 있도록 학습됩니다.

  • D(x)는 입력된 x가 실제 데이터일 확률을 반환합니다. 이상적으로는, x가 실제 데이터에서 sampling된 데이터라면 1의 값을, 생성된 이미지에서 sampling된 허구의 데이터라면 0의 값을 반환합니다.
  • $x$ ~ $p_{data(x)}$는 실제 데이터의 분포에서 데이터 x를 sampling한다는 의미입니다. 목적함수가 D의 관점에서 높은 값을 도출해야하므로 $E_{x\sim p_{data}(x)}[logD(x)]$는 실제 데이터 분포에서 sampling된 데이터에 대해서 높은 값인 1에 가까운 값을 반환할 수 있도록 학습이 진행됨을 의미합니다.
    
    

• 목적함수 V(D,G)는 생성기(G) 관점에서 낮은 값을 가질 수 있도록 학습됩니다.

  • 생성기(G)는 Latent vector, noise vector를 입력받아 실제 데이터를 변형하여 데이터를 생성합니다. $z\sim p_z(z)$는 noise z를 sampling함을 의미하며, G(z)는 생성기가 noise를 입력받아 데이터를 생성함을 의미합니다.
  • $E_{z\sim p_z(z)}[log(1-D(G(z))]$는 noise z를 입력받아 생성된 이미지를 판별기(D)에 의해 판별되는 과정을 의미합니다. 생성기(G)의 관점에서 목적함수는 작은 값을 가져야하므로 1-D(G(z))가 작은 값을 가지도록, 즉 D(G(z))가 1에 가까운 큰 값을 가지도록 학습됩니다.
  • 따라서, noise z의 입력으로 생성된 이미지를 판별기(D)가 실제 데이터 분포에서 sampling되었다고 착각할 수 있을 만큼 사실적이고 정교하게 만들어지도록 설정되며, 앞서 말씀드린 대로 판별기(D) 관점에서 목적함수는 큰 값을 가져야하므로 생성된 허구의 데이터를 허구의 데이터라 분류하여 0에 가까운 값을 반환할 수 있도록 학습됩니다.

3.2 그래프 표현

• 목적 함수를 그래프로 표현하면 다음과 같이 표현될 수 있습니다.
  
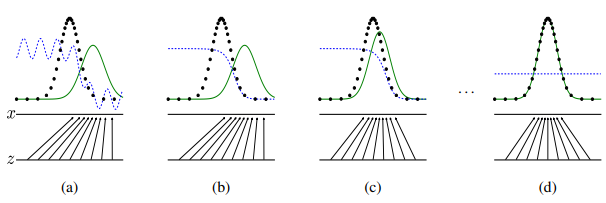
  • blue line : Disciriminative distribution (판별기 반환값의 분포)
  • black line : 실제 데이터의 분포
  • green line : Generative distribution (생성된 데이터의 분포)
    
    
• 학습 초기(a)에 생성된 데이터의 분포는 실제 데이터의 분포와 차이가 크며 판별기 또한 부분적으로 정확한 판별을 시행합니다.
• 학습이 진행되며 생성된 데이터의 분포는 실제 데이터의 분포와 유사해지도록 학습되며 학습이 충분히 이루어진 상황(d)에서는 판별기가 실제 데이터와 생성된 데이터를 구분하지 못하는 상태, D(x) = 0.5의 값이 반환하도록 학습됩니다.

4. 이론적 증명

명제1 : optimal D는 G가 고정되어있을 때, $D^*_G(x) = \frac{p_{data}(x)}{p_{data}(x) + p_g(x)}$로 수렴한다.

• GAN 모델의 목적함수인

  

  는 다음과 같이 변환될 수 있습니다.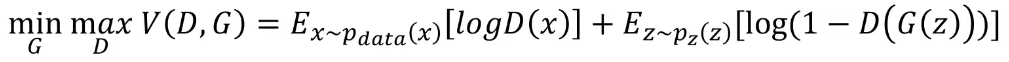

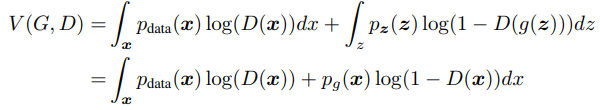
연속 변수의 기대값

• $E[X] = \int xf(x)dx$

• 목적함수는 D의 관점에서 최대의 값을 가져야하며, D의 Optimal은 마지막으로 변환된 식의 극대값을 가지게 됩니다.
• 마지막으로 변환된 목적함수의 식은 $Alog(x) + Blog(1-x)$의 형태이며 이 형태의 식의 극대값은 $\frac{A}{A+B}$를 가지게 됩니다. 따라서 Optimal D는 $D^*_G(x) = \frac{p_{data}(x)}{p_{data}(x) + p_g(x)}$의 값을 가지게 됩니다.

  $y = Alog(x) + Blog(1-x)$
  $y' = \frac{A}{x} - \frac{B}{1-x} = \frac{A - Ax - Bx}{x(1x)}$
  $x = \frac{A}{A+B}$

명제2 : Global optimum은 $p_g = p_{data}$

• 명제는 두 데이터 분포의 차이와 관련되어 있으며, 두 데이터 분포의 차이를 나타내는 것에는 KL Divergence와 JSD 등이 있습니다. GAN 모델에서는 JSD를 이용하여 명제를 증명합니다.

  Entropy

  • 정보 이론에서 정보량, 무질성의 정도를 나타냅니다.
  • Entropy는 $H(P) = -\sum^N_{i=1}E_{P\sim X}[h(x)] = -\sum^N_{i=1}p_ilogp_i$ (N : Class 개수, $p_i$ :발생확률)로 표현되며 entropy의 값이 0에 가까울수록 정보량이 작음을 의미합니다.
    예를 들어 모든 경우의 발생 확률이 같은 경우, 즉 불확실성이 큰 경우는 Entropy의 값이 커지며 이 데이터에서 얻을 수 있는 정보량이 큼을 의미합니다.

  Cross Entropy

  • ML/DL에서 알고 있는 실제 데이터의 분포 P와 예측 모델을 통해 구한 데이터의 분포 Q를 이용하여 Entropy를 구하고, 이를 통해 예측 모델이 실제 데이터의 분포와 유사해지도록 학습하는 과정에 사용됩니다.
  • Cross Entropy는 $H(P, Q) = -E_{X\sim P}[-logQ(x)] = -\sum_xP(x)logQ(x)$로 표현됩니다.

  KL Divergence

  • 서로 다른 두 분포의 차이를 측정하는데 사용됩니다.
  • $D_{KL}(P||Q) = \sum_xP(x)log(\frac{P(x)}{Q(x)})$의 식을 통해 두 분포의 차이를 구하게 됩니다.
  • 식을 $D_{KL}(P||Q) = -H(P,P) + H(P,Q)$로 변환할 수 있으며 두 데이터 분포의 정보량, 즉 H(P, Q)는 $D_{KL}(P||Q) + H(P)$로 표현할 수 있습니다.

  JSD(Jenson-Shanon divergence)

  • M을 확률 분포 P, Q의 평균이라고 할 때, JSD는 다음과 같이 표현할 수 있습니다.
  • $JSD(P||Q) = \frac{1}{2}KL(P||M) + \frac{1}{2}KL(Q||M)$
  • M이 P와 Q의 평균값이므로 KL Divergence와는 다르게 대칭적이고, 거리의 개념을 적용할 수 있습니다.

• D의 관점에서 V의 값을 최대로 만드는 함수를 새로이 C(G)로 정의한다면, 명제 1의 결론을 적용하여 다음과 같이 식을 표현할 수 있습니다.
  
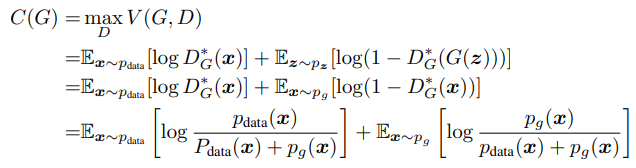
• GAN 모델에서는 명제를 증명하기 위하여 JSD를 사용합니다. JSD를 적용한 수식의 편의를 위하여 각각의 식에 log2를 더하고 다시 2log2(=log4)를 빼는 과정을 거쳐 다음과 같은 식을 얻습니다.
  
  
• 중간 과정을 제외하면 $C(G) = -log4 + 2D_{JSD}(p_{data}||p_g)$의 식을 얻을 수 있습니다. C(G)는 목적함수를 새롭게 정의한 함수이며 G의 관점에서 목적함수를 작게 만드는 과정이 남아있습니다.
• 위에서 언급한 바대로, JSD는 거리의 개념을 적용할 수 있기에 $D_{JSD}(p_{data}||p_g)$는 0을 최소값으로 가질 수 있습니다. 0을 최소값으로 가지게 되면 G와 D의 관점에서 Global optimum을 가지게 됩니다.
• 따라서 $D_{JSD}(p_{data}||p_g)$가 0이 되는 지점, $p_g = p_{data}$일 때 GAN모델은 Global optimum을 가지게 됩니다.