응용통계학 - Random variables

Probability Mass Function(PMF, 확률질량함수)

Random variable

• 확률변수는 특정 실험의 각각의 결과에 numerical value를 할당함으로써 얻어진다.
  

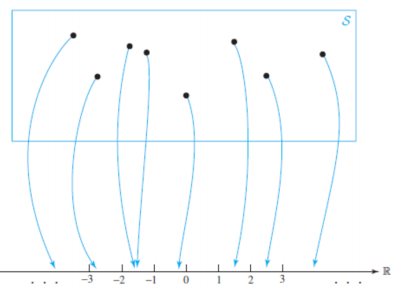
PMF

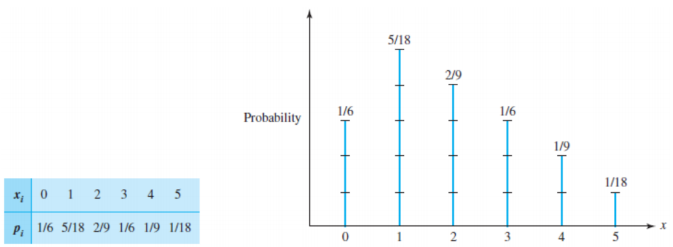
• 확률질량함수는 Random variable X에 각각의 확률을 부여한다.
• 각각의 확률은 0에서 1의 값을 가지며 총 확률의 합은 1이다.
• 이산확률변수에 관하여 적용된다.
• $P(X = x_{i}) = p_{i}$
  

Probability Density Function

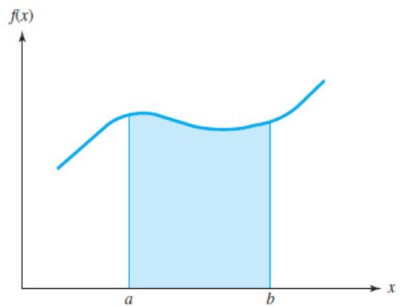
• 연속확률변수에 대하여 사용된다.
• $\int_{statespace} f(x)dx = 1$
• 두 값 사이에 놓인 확률변수에 대한 확률을 구한다.
  

Cumulative Distribution Function(CDF, 누적분포함수)

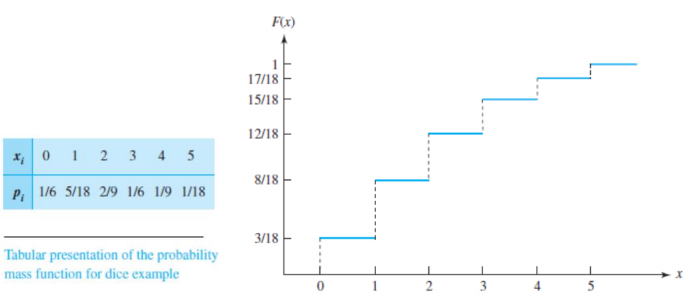
• $F(x) = \sum_{y:y<=x}P(X=y)$
• x보다 작은 값을 가지는 y 값에 대한 확률 값을 더하여 나타낸다.

이산확률변수의 경우

연속확률변수의 경우

• 연속확률변수의 누적분포함수 F(x)는 nondecreasing 함수 형태를 가지며 0에서 시작하여 1까지 우상향으로 나타난다.

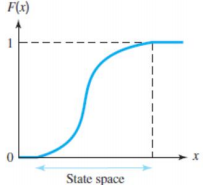
• 누적분포함수는 확률밀도함수와 마찬가지로 연속확률변수의 확률값을 더하여 나타내기에 CDF와 PDF는 상호 구축가능하다.
• $F(x) = P(X<=x) = \int^x_{-\infin}f(y)dy$
• $f(x) = {dF(x) \over dx}$
• $P(a <= X <= b) = P(X <= b) - P(X<=a) = F(b) - F(a)$

Expectation

• 기댓값, 평균 등으로 표현한다.
• E(X) : expectation of X

기대값 : 이산확률변수의 경우

• $P(X=x_i) = p_i$ 일 때 $E(X) = \sum_ip_ix_i$

기대값 : 연속확률변수의 경우

• $E(X) = \sum_{state space}xf(x)dx$

Median

• median이라 middle value를 지칭한다.
• F(x) = 0.5

Measure of Spread

Variance(분산)

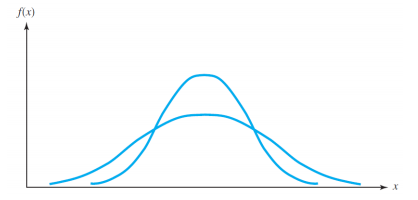
• mean value에 대하여 확률변수의 deviation 또는 measures the spread
• 항상 양수 값을 가진다.
• 높은 variance값은 더 많이 퍼져있음을 의미한다.
• 이산확률변수의 경우
• $Var(X) = E((X-E(X))^2) = E(X^2) - (E(X))^2$

Standard Deviation(표준 편차)

• positive square root of the variance
• 분산은 $\sigma^2$로 표현되며 표준편자는 $\sigma$로 표현된다.

Percentiles

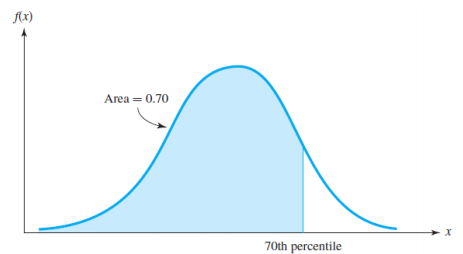
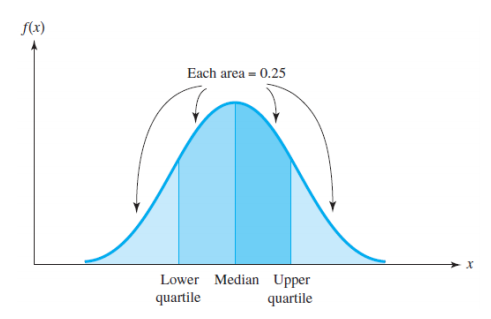
• The 𝑝 × 100th quantile of a random variable X with a cumulative distribution function 𝐹 𝑥 is defined to be the value x for which $F(x) = p$

Independence

• 하나의 확률변수의 확률이 다른 확률변수의 발생에 영향을 미치지 않을 때 독립적이라고 정의한다.

이산확률변수의 경우

• $p_{ij} = p_{i+}p_{+j}$

연속확률변수의 경우

• $f(x,y) = f_X(x)f_Y(y)$

Covariance (공분산)

• 두 확률변수가 의존적일 때 공분산을 이용하여 두 확률변수의 의존 정도를 표현한다.
• 양수와 음수 모두를 값으로 가질 수 있으며 독립의 경우에는 0의 값을 가진다.
• $COV(X,Y) =E((X-E(X))(Y-E(Y))) = E(XY) - E(X)E(Y)$

Correlation

• 두 확률 변수의 의존성을 나타내는 더 편한 방법으로 상관관계를 사용할 수 있다,
• -1과 1 사이의 값을 가진다.
• $Corr(X,Y) = {Cov(X,Y) \over \sqrt{Var(X)Var(Y)}}$

Linear functions of RV

• Y = aX + b라고 할 때
• $E(Y) = aE(X) + b$
• $Var(Y) = a^2Var(X)$

• $E(X_1 + X_2) = E(X_1) + E(X_2)$
• $Var(X_1 + X_2) = Var(X_1) + Var(X_2) + 2Cov(X_1,X_2)$

Averaging Independent RVs

• $\bar X = {X_1 + ... + X_n \over n}$
• $E(\bar X) = \mu$
• $Var(\bar X) = {\sigma^2 \over n}$