이제 ! 탐색1을 끝마쳤으므로 탐색2를 배워보자.
제일 첫 챕터는
균형 잡힌 이진 탐색 트리 : AVL트리의 이해
이다.
이진 탐색 트리의 문제점과 AVL트리
이진 탐색 트리의 탐색 연산은 로그이엔의 시간 복잡도를 가지지만..균형이 맞지 않게 쌓여수록 빅오는 n에 가까운 시간 복잡도를 보인다.

그림을 보면 노드의 수 만큼 높이가 형성된거와 같이 매우 불균형해보인다!
그런데 3만 미리 저장하고 이후 순서대로 넣으면
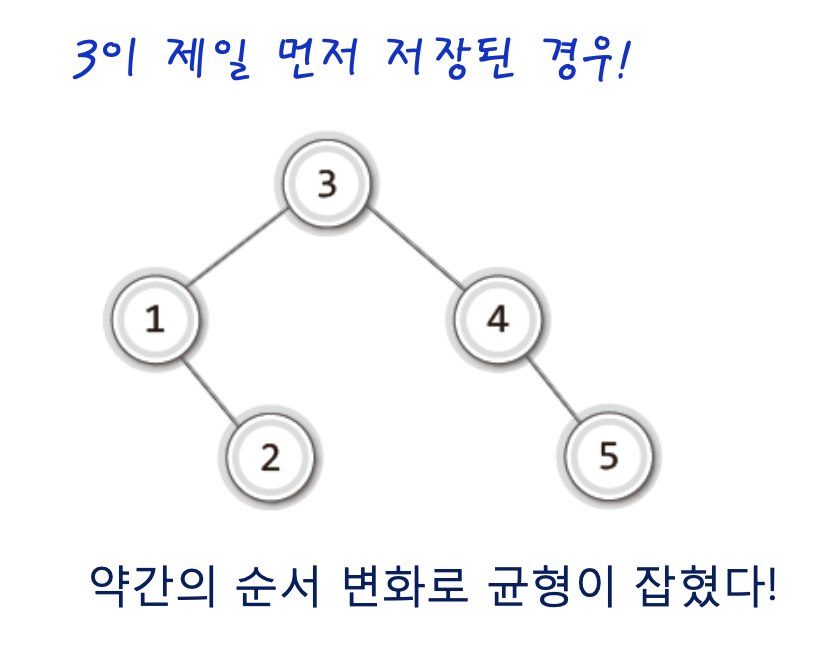
보이는가!
3만 먼저 저장해도 균형이 잡히게 된다.
이렇듯 앞서 보인 이진 탐색트리는 저장 순서에 따라 탐색의 성능에 큰 차이를 보인다.
이것이 바로 이진 탐색 트리의 단점이다.
이러한 단점을 해결한 트리를 가리켜 "균형 잡힌 이진 트리"라 할수있다.
그 종류는 대략
- AVL 트리
- 2-3 트리
- 2-3-4 트리
- Red-Black 트리
- B 트리
이 중 하나를 선택해 우리가 앞서 만든 이진 탐색 트리가 자동으로 균형을 잡을 수 있도록 개선해보자!
그러한 목적으로 AVL트리를 선택했다.
자동으로 균형을 잡는 AVL 트리와 균형 인수(Balance Factor)
AVL트리는 Adelson-Velskii 와 Landis에 의해 1960년대에 고안되어 이들 이름을 따 AVL트리라고 이름지어졌다.(1960...년..오진당...)
AVL트리는 노드가 추가될 떄, 삭제될 때 트리의 균형상태를 파악해서 스스로 그 구조를 변경하여 균형을 잡는 멋진 트리이다.
균형의 정도를 표현하기위해 "균형 인수"라는 것을 사용하는데 이것은
균형 인수 = 왼쪽 서브트리 높이 - 오른쪽 서브 트리 높이
이다.
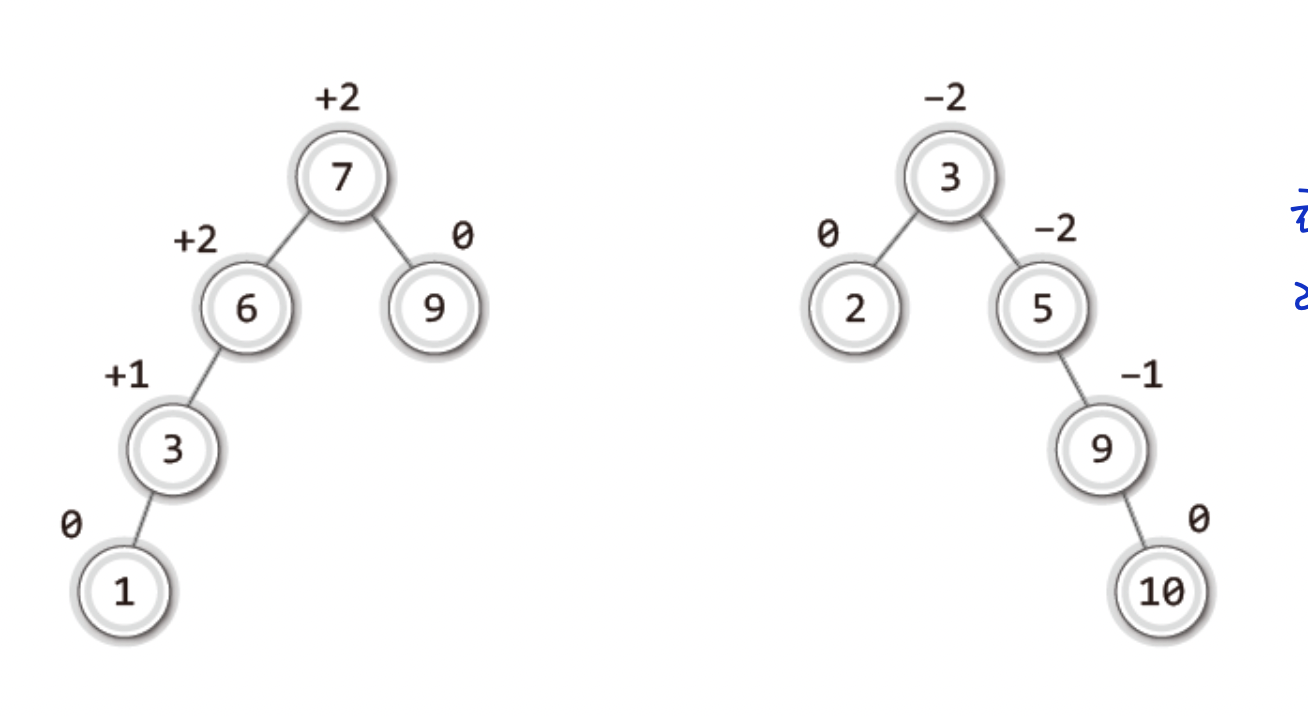
노드 별 균형 인수이다 !
이를 알았으니 리밸런싱(균형을 잡기 위한 트리 구조의 재조정) 시기를 짐작할 수 있을것이다!!
균형 인수의 절댓값이 크면 클수록 그만큼 트리의 균형이 무너진 상태이다.
그러므로! 균형 인수의 절댓값이 2 이상인 경우에 균형을 잡기 위한 트리의 재조정을 진행해야한다!
리밸런싱이 필요한 첫 번째 상태와 LL회전
트리의 균형이 무너지는 상태는 4가지로 정리가 된다.
그러니 ! 각 상태별로 리밸런싱 방법에도 차이가 있다.
첫번째
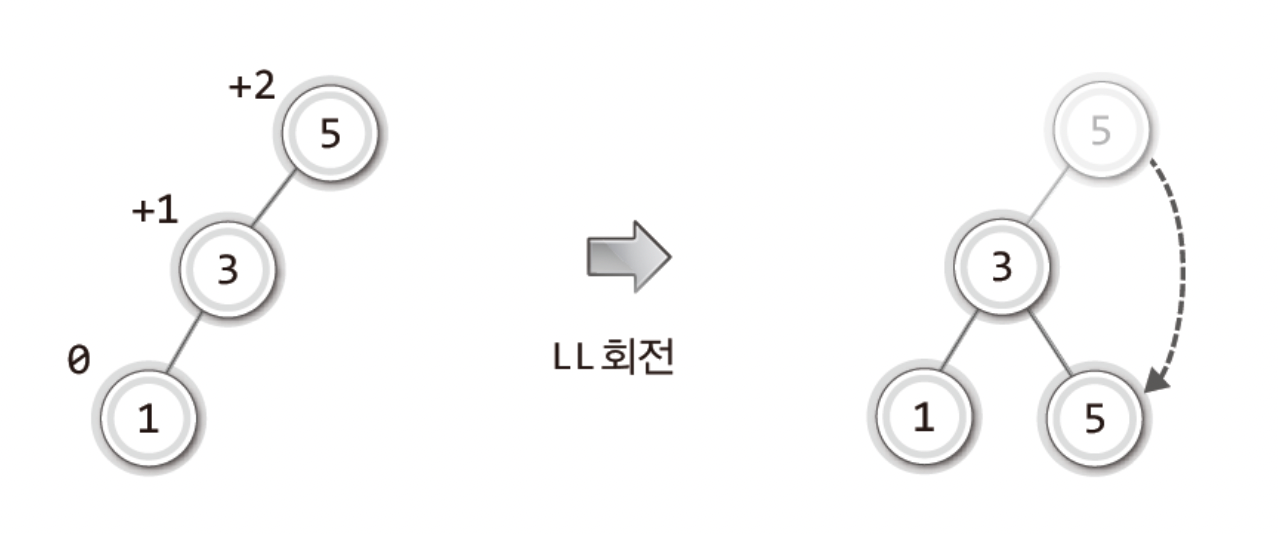
이를 보면 어떻게 표현할것인가?
"5가 저장된 노드의 왼쪽에 3이 저장된 자식 노드가 하나 존재하고, 그 자식 노드의 왼쪽에 1이 저장된 자식 노드가 또 하나 존재한다."
사실 이는 매우 엉성한 표현이지만! 이를 다시보면
다음과 같은 사실을 알 수 있다.
"핵심은 자식 노드 두 개가 왼쪽으로 연이어 연결되어 균형 인수가 +2가 연출되었다는 것이다."
이제 어느정도 눈치가 있다면 LL회전이 무엇을 의미하는지 알겠는가!?
아직도 모른다면 눈치제로다!!
바러 Left Left 회전이다
즉!
균형 인수가 +2인 상태는 "Left Left 상태" 이고 이를 줄여 "LL상태"라고 하는것이다.
그리고 이러한 불균형의 해소를 위해 등장한 리밸런싱 방법을 가리켜 "LL회전"이라 한다.
즉!!!
왼쪽으로 두번 돌린다는 뜻이 아니고, LL상태에서 균형을 잡기 위해 필요한 회전!
이라는 의미이다.
LL회전의 핵심은
균형 인수가 +2인 노드를 균형 인수가 +1인 노드의 오른쪽 자식노드가 되게 하는데 있다.
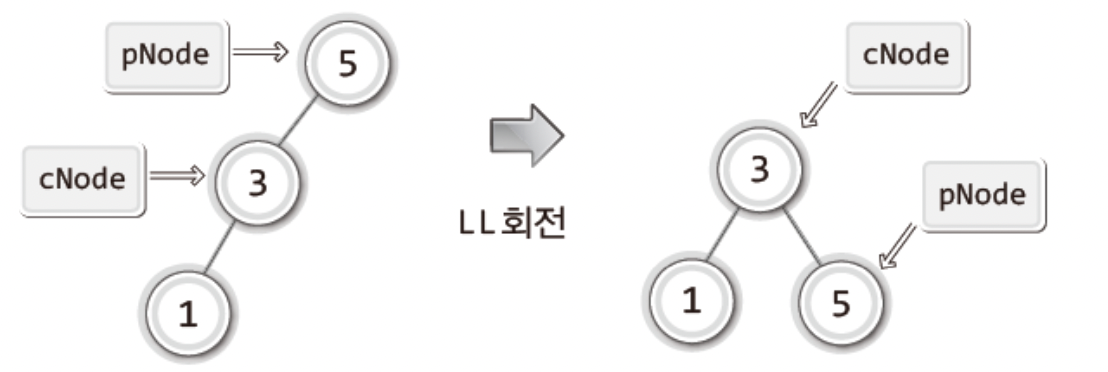
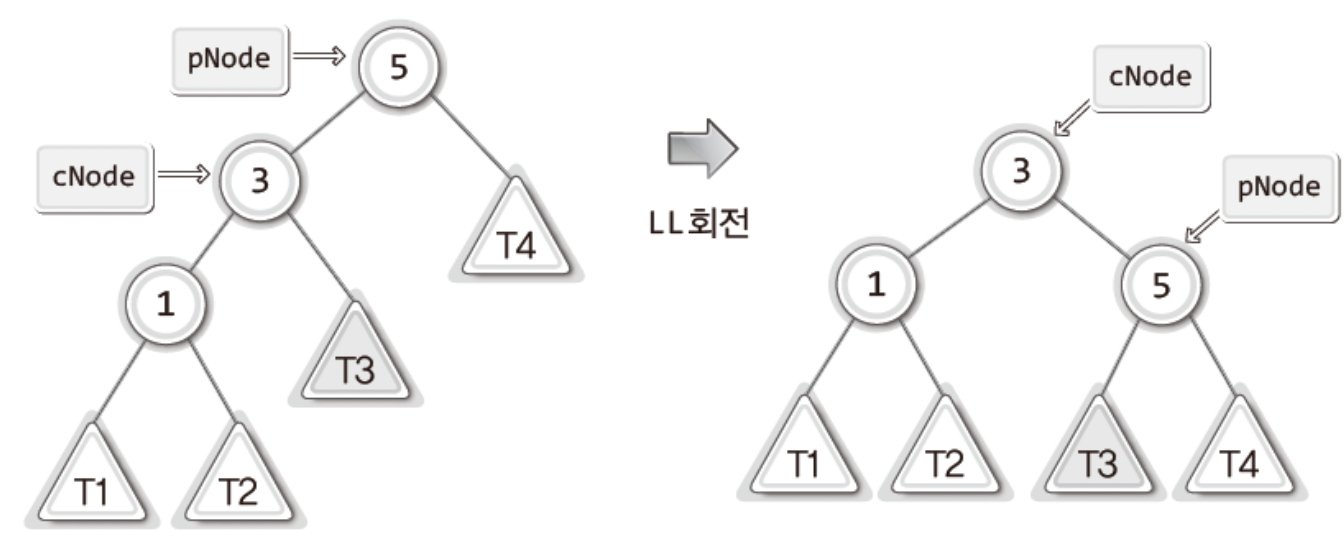
이러한 간단한 트리를 보면 그저ChangeRightSubTree(cNode,pNode); 를 하면 되지만..
일반화를 하면 위의 한 문장으로만은 부족하다.
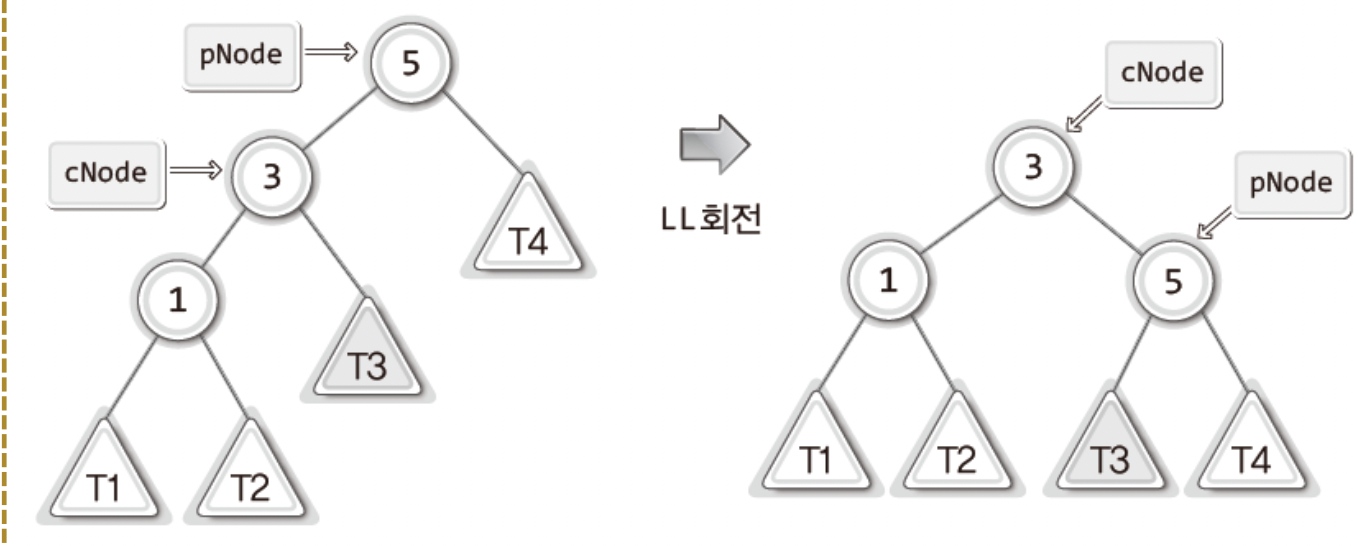
위 그림의 T1,2,3,4를 높이가 동일한 서브 트리라고 가정하자!
그렇다면 5와3이 저장된 노드의 균형 인수에 영향을 미치지 않는다.
그러므로 여전히 LL상태에 해당한다.
T1,2,3,4를 NULL로 치환하면 앞선 그림의 LL상태가 된다!
그렇기에 위의 그림은 LL상태를 일반화한 것으로 볼 수 있다.
이제 일반화 상태에서 LL회전을 위해 추가로 고민해야할 것은 바로 ! T3이다!
T1,2,4는 고민없이 그저 부모노드를 따라다니고 따라다닌다고 해도 문제가없지만
T3의 부모 노드는 루트노드가 될 분이다!
따라서 T3은 그 자리를 다른 노드에게 양보해야 한다.
위의 그림에서는 당연빠따로 5에게 양보한다 !
양보한후 T3은 어디가야할것 같은가?
바로!!!!
5가 저장된 노드의 왼쪽 자식 노드이다!
이제 이 논리대로 회전한 그림을 보여주겠다.
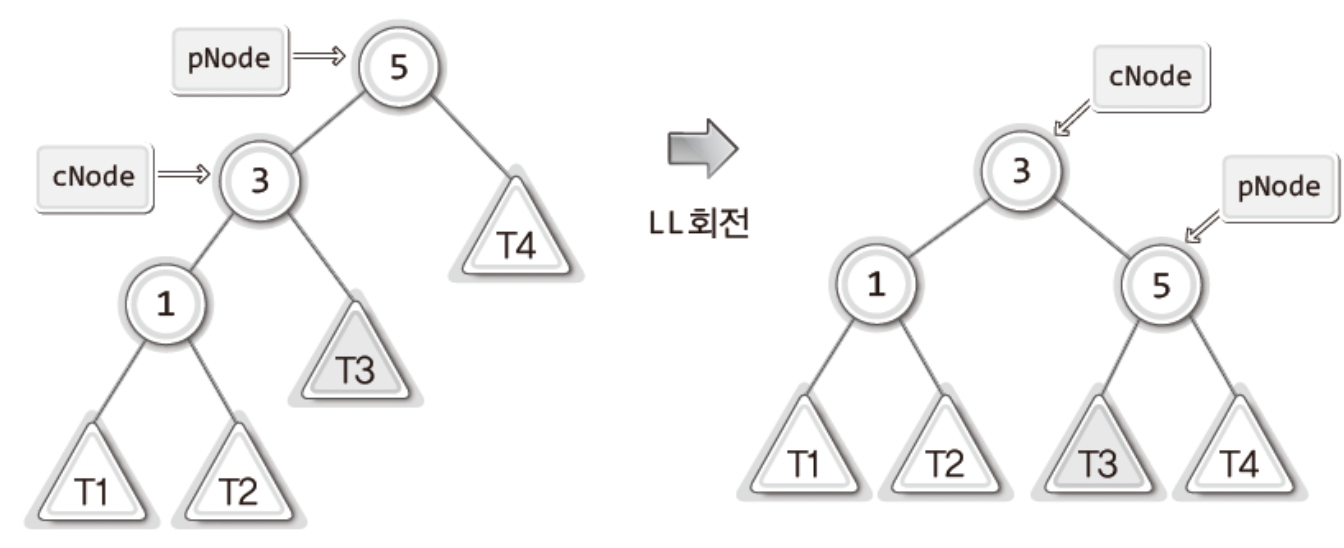
그러므로
cNode가 가리키는 오른쪽 서브 트리를 pNode가 가리키는 노드의 왼쪽 서브 트리로 옮기기 위해서는 다음 문장을 실행해야한다!
ChangeLeftSubTree(pNode,GetRightSubTree(cNode));
그러므로!!
LL회전을 위해서는
다음 두 문장을 순서대로 실행해야한다.
ChangeLeftSubTree(pNode,GetRightSubTree(cNode));
ChangeRightSubTree(cNode,pNode);이제 네번째 중 두번째 상태를 다음 포스트에서 보자