
이진 탐색 트리의 삭제구현 : 삭제의 구현을 위한 이진 트리의 확장
이를 구현 하기 위해 BinaryTree2.h,c에 다음 4개의 함수를 추가로 선언 및 정의하자
//왼쪽 자식 노드를 트리에서 제거, 제거된 노드의 주소 값으 반환한다.
BTreeNode * RemoveLeftSubTree(BTreeNode * bt);
// 오른쪽 자식 노드를 트리에서 제거, 제거된 노드의 주소 값이 반환.
BTreeNode * RemoveRightSubTree(BTreeNode * bt);
// 메모리 소멸을 수반하지 않고 main의 왼쪽 자식 노드를 변경한다.
void ChangeLeftSubTree(BTreeNode * main, BTreeNode * sub);
// 메모리 소멸을 수반하지 않고 main의 오른쪽 자식 노드를 변경한다.
void ChangeRightSubTree(BTreeNode * main, BTreeNode * sub);
우선 BinaryTree2.c 는 이진 탐색 트리 구현에 충분한 도구가 되지는못하는데 그 이유는 다음 두 가지이다.
- 노드의 제거에 대한 기능이 정의되지 않았다.
- MakeLeftSubTree, MakeRightSubTree 함수는 교체되는 노드의 소멸까지 진행한다.
소멸은 교체를 목적으로는 어울리지않기에 우리는 다음 두 함수를 추가로 정의해야한다.
ChangeLeft/RightSubTree를 정의해보자
// 메모리의 소멸을 수반않고 main의 왼쪽 자식 노드를 변경한다
void ChangeLeftSubTree(BTreeNode * main, BTreeNode * sub)
{
main->left = sub;
}
// 메모리의 소멸을 수반않고 main의 오른쪽 자식 노드를 변경한다
void ChangeRightSubTree(BTreeNode * main, BTreeNode * sub)
{
main->right = sub;
}이제 남은 삭제함수를 보자
//왼쪽 자식 노드 제거
BTreeNode * RemoveLeftSubTree(BTreeNode * bt)
{
BTreeNode * delNode;
if(bt != NULL)
{
delNode = bt->left;
bt->left =NULL;
}
return delNode;
}
//오른쪽 자식 노드 제거
BTreeNode * RemoveRightSubTree(BTreeNode * bt)
{
BTreeNode * delNode;
if(bt != NULL)
{
delNode = bt->right;
bt->right =NULL;
}
return delNode;
}
삭제라고하면 보통 메모리의 해체 까지 생각하겠지만
"삭제"와 "메모리 해체"는 별개의 것이다.
솔직히 말하자면 삭제과정에서 메모리의 해체를 포함하지않는것이 일반적이고 대신 삭제할 메모리의 주소 값을 반환해서 메모리의 해체에 대한 책임을 함수를 호출한 영역으로 넘기고 있다.
이렇게 BinaryTree2.h,c에 함수들을 추가하고 이런 생각이 들지 모른다.
"처음부터 걍 추가하지 왜 이제 와서 추가함?"
하지만 ! 이렇게 내가 사용할 기능들을 미리 예측해서 도구를 만드는것은 쉽지않고 이것이 옳은것만이 아니다!
오히려! 필요에 따라 도구를 확장하고 수정해 나가는 것이 현명한 방법이다.
이제 수정한 소스코드와 헤더파일을 보이겠다.
#ifndef __BINARY_TREE2_H__
#define __BINARY_TREE2_H__
typedef int BTData;
typedef struct _bTreeNode
{
BTData data;
struct _bTreeNode * left;
struct _bTreeNode * right;
} BTreeNode;
BTreeNode * MakeBTreeNode(void);
BTData GetData(BTreeNode * bt);
void SetData(BTreeNode * bt, BTData data);
BTreeNode * GetLeftSubTree(BTreeNode * bt);
BTreeNode * GetRightSubTree(BTreeNode * bt);
void MakeLeftSubTree(BTreeNode * main, BTreeNode * sub);
void MakeRightSubTree(BTreeNode * main, BTreeNode * sub);
typedef void VisitFuncPtr(BTData data);
void PreorderTraverse(BTreeNode * bt, VisitFuncPtr action);
void InorderTraverse(BTreeNode * bt, VisitFuncPtr action);
void PostorderTraverse(BTreeNode * bt, VisitFuncPtr action);
//왼쪽 자식 노드를 트리에서 제거, 제거된 노드의 주소 값으 반환한다.
BTreeNode * RemoveLeftSubTree(BTreeNode * bt);
// 오른쪽 자식 노드를 트리에서 제거, 제거된 노드의 주소 값이 반환.
BTreeNode * RemoveRightSubTree(BTreeNode * bt);
// 메모리 소멸을 수반하지 않고 main의 왼쪽 자식 노드를 변경한다.
void ChangeLeftSubTree(BTreeNode * main, BTreeNode * sub);
// 메모리 소멸을 수반하지 않고 main의 오른쪽 자식 노드를 변경한다.
void ChangeRightSubTree(BTreeNode * main, BTreeNode * sub);
#endif
BinaryTree.c
#include <stdio.h>
#include <stdlib.h>
#include "BinaryTree2.h"
BTreeNode * MakeBTreeNode(void)
{
BTreeNode * nd = (BTreeNode*)malloc(sizeof(BTreeNode));
nd->left = NULL;
nd->right = NULL;
return nd;
}
BTData GetData(BTreeNode * bt)
{
return bt->data;
}
void SetData(BTreeNode * bt, BTData data)
{
bt->data = data;
}
BTreeNode * GetLeftSubTree(BTreeNode * bt)
{
return bt->left;
}
BTreeNode * GetRightSubTree(BTreeNode * bt)
{
return bt->right;
}
void MakeLeftSubTree(BTreeNode * main, BTreeNode * sub)
{
if(main->left != NULL)
free(main->left);
main->left = sub;
}
void MakeRightSubTree(BTreeNode * main, BTreeNode * sub)
{
if(main->right != NULL)
free(main->right);
main->right = sub;
}
void PreorderTraverse(BTreeNode * bt, VisitFuncPtr action)
{
if(bt == NULL)
return;
action(bt->data);
PreorderTraverse(bt->left, action);
PreorderTraverse(bt->right, action);
}
void InorderTraverse(BTreeNode * bt, VisitFuncPtr action)
{
if(bt == NULL)
return;
InorderTraverse(bt->left, action);
action(bt->data);
InorderTraverse(bt->right, action);
}
void PostorderTraverse(BTreeNode * bt, VisitFuncPtr action)
{
if(bt == NULL)
return;
PostorderTraverse(bt->left, action);
PostorderTraverse(bt->right, action);
action(bt->data);
}
// 메모리의 소멸을 수반않고 main의 왼쪽 자식 노드를 변경한다
void ChangeLeftSubTree(BTreeNode * main, BTreeNode * sub)
{
main->left = sub;
}
// 메모리의 소멸을 수반않고 main의 오른쪽 자식 노드를 변경한다
void ChangeRightSubTree(BTreeNode * main, BTreeNode * sub)
{
main->right = sub;
}
//왼쪽 자식 노드 제거
BTreeNode * RemoveLeftSubTree(BTreeNode * bt)
{
BTreeNode * delNode;
if(bt != NULL)
{
delNode = bt->left;
bt->left =NULL;
}
return delNode;
}
//오른쪽 자식 노드 제거
BTreeNode * RemoveRightSubTree(BTreeNode * bt)
{
BTreeNode * delNode;
if(bt != NULL)
{
delNode = bt->right;
bt->right =NULL;
}
return delNode;
}이제 완전한 구현을 해보자 !
이진 탐색트리의 삭제구현: 완전한 구현
이를 위해 기존에 만들었던
BinarySearchTree.c,h를 확장해보자 !
BinarySearchTree2.h
//
// BinarySearchTree.h
// BinarySearchTree
//
// Created by 서희찬 on 2021/04/17.
//
#ifndef BinarySearchTree_h
#define BinarySearchTree_h
#include "BinaryTree2.h"
typedef BTData BSTData;
//BST의 생성 및 초기화
void BSTMakeAndInit(BTreeNode ** pRoot);
// 노드에 저장된 데이터 반환
BSTData BSTGetNodeData(BTreeNode * bst);
// BST를 대상으로 데이터 저장(노드의 생성과정 포함)
void BSTInsert(BTreeNode ** pRoot, BSTData data);
// BST를 대상으로 데이터 탐색
BTreeNode * BSTSearch(BTreeNode * bst, BSTData target);
// 트리에서 노드를 제거하고 제거된 노드의 주소 값을 반환한다.
BTreeNode * BSTRemove(BTreeNode ** pRoot, BSTData Target);
// 이진 탐색 트리에 저장된 모든 노드의 데이터를 출력한다.
void BSTShowAll(BTreeNode * bst);
#endif /* BinarySearchTree_h */
소스코드의 삭제함수를 보자
dNode = cNode; // 삭제 대상을 dNode가 가리키게 한다.
// 첫 번째 경우 : 삭제 대상이 단말 노드인 경우
if(GetLeftSubTree(dNode) == NULL && GetRightSubTree(dNode)== NULL)
{
if(GetLeftSubTree(pNode)== dNode)
RemoveLeftSubTree(pNode);
else
RemoveRightSubTree(pNode);
}
// 두 번째 경우 : 삭제 대상이 하나의 자식노드를 갖는 경우
else if(GetLeftSubTree(dNode) == NULL || GetRightSubTree(dNode)== NULL)
{
BTreeNode * dcNode; // 삭제 대상의 자식 노드 가리킴
if(GetLeftSubTree(dNode) != NULL)
dcNode = GetLeftSubTree(dNode);
else
dcNode = GetRightSubTree(dNode);
if(GetLeftSubTree(pNode) == dNode)
ChangeLeftSubTree(pNode, dcNode);
else
ChangeRightSubTree(pNode, dcNode);
}
// 세 번째 경우 : 두 개의 자식 노드를 모두 갖는 경우
else
{
BTreeNode *mNode = GetRightSubTree(dNode); // 대체 노드를 가리킨다.
BTreeNode * mpNode = dNode; // 대체 노드의 부모 노드를 가리킨다.
int delData;
//삭제 대상의 대체 노드를 찾는다.
while (GetLeftSubTree(mNode)!=NULL) {
mpNode = mNode;
mNode = GetLeftSubTree(mNode);
}
// 대체 노드에 저장된 값을 삭제할 노드에 대입한다.
delData = GetData(dNode); // 대입 전 데이터 백업
SetData(dNode,GetData(mNode)); // 대입!
// 대에 노드의 부모 노드와 자식 노드를 연결한다.
if(GetLeftSubTree(mpNode) == mNode)
ChangeLeftSubTree(mpNode, GetRightSubTree(mNode));
else
ChangeRightSubTree(mpNode, GetRightSubTree(mNode));
dNode = mNode;
SetData(dNode, delData); // 백업 데이터 복원
}
// 삭제된 노드가 루트 노드인 경우에 대한 추가적인 처리
if(GetRightSubTree(pVRoot)!=*pRoot)
*pRoot = GetRightSubTree(pVRoot); // 루트 노드의 변경을 반영
free(pVRoot); // 가상 루트 노드의 소멸
return dNode; // 삭제 대상의 반환
}
상당히..길다.
이는 1,2,3 가지 상황에 따라 나눠주기 때문이다.
이제 자세히 한번봐보쟝..
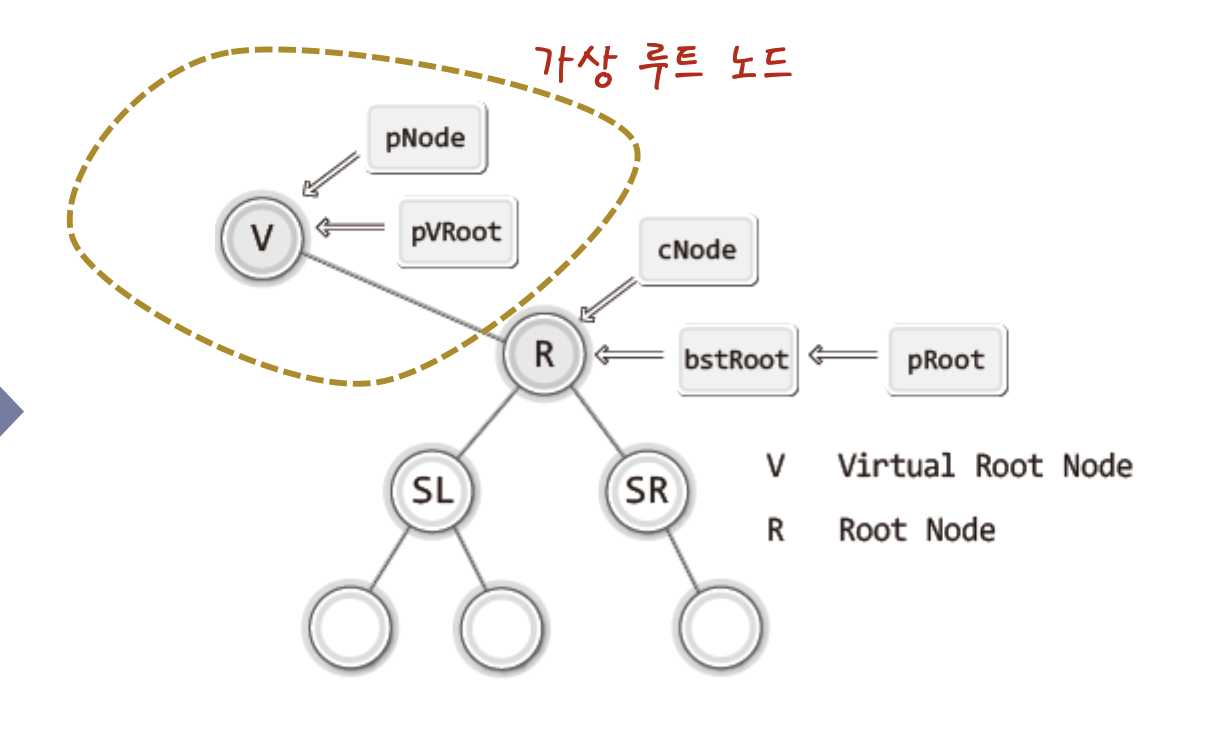

pRoot에는 "루트 노드를 가리키는 포인터 변수의 주소 값"이 담긴다.
위 그림에서 보이듯 V라는 노드를 하나 생성 한 후, 실제 루트 노드인 R이 V의 오른쪽 자식 노드가 되게 하고 있다.
이렇듯 가상 노드를 둔 이유는
"삭제할 노드가 루트 노드인 경우의 예외적인 삭제흐름을 일반화 하기 위함이다."
이 이유는 삭제 대상이 루트노드인 경우 삭제의 방법을 조금 달리해야하기 때문이다
위 그림을 보면 cNode가 가리키는 노드의 부모 노드를 pNode가 가리키고 있는데, 이 관계는 삭제과정 내내 유지되어야 한다.
이 이유는
"삭제할 노드를 cNode가 가리키게 되는데, 삭제의 과정에서 cNode의 부모와 자식을 연결시키는 과정이 등장하는 경우가 있다.
때문에 cNode의 부모 노드를 언제든 가리키고 있어야 한다.
삭제의 과정에서 삭제할 노드의 부모와 자식을 연결시키는 경우가 있음을 기억하고 있을것이다!!!
그런데..
루트노드에 부모노드가 있냐?!
없다!!
띠리사 이게 문제가 되어 루트 노드의 삭제과정은 조금 달라질 수밖에 없지만! 가상루트노드를 둔다면 루트 노드를 삭제하는 경우에도 위 함수의 if--else if ---else 구문을 그대로 활용할 수 있다.
그럼이제 다음 반복문을 보자 !

위의 반복문을 보고 이와 같은 생각을 잠시 했을 수도 있다.
"노드의 탐색을 위한 BSTSearch 함수가 정의되어있는데 왜 사용안하고 별도의 반복문을 구성한거지?
위의 반복문을 실행하면 cNode는 삭제할 노드를 가리키게 되는데..
이것이 전부라면 cNode = BSTSearch(*pRoot,target);을 해도 되지만!
이렇게 해서는 cNode의 부모노드를 pNode가 가리키게 할 수 없다!!! 그렇기에 이렇게 반복문을 구성해야한다.
이제 마지막 if문에 대해 분석하장
그 중간에 if---else if--else는 3가지 상황에 대한 삭제과정이다.

삭제 대상이 루트 노드인 경우, 루트 노드의 다른 노드로 대체되기도한다!
이렇게 루트 노드가 대체되고 나면, 매개 변수인 pRoot가 가리키는 포인터 변수는 더 이상 이진 탐색트리의 루트 노드를 가리키지 않게 된다.
BUT!!
삭제 연산 후에도 이 포인터 변수는 루트 노드를 가리켜야 한다!
그러므로 마지막 if문을 삽입 한것이다.
이제 새로운 함수를 보이겠다.
void ShowIntData(int data)
{
printf("%d ", data);
}
void BSTShowAll(BTreeNode * bst)
{
InorderTraverse(bst, ShowIntData); //중위 순회
}그렇다! 중위 순회를 통해 이진 탐색 트리에 저장된 모든 데이터를 출력 하기 위해 정의된 함수들이다.
이제 마지막으로 main 함수를 소개하고 출력하고 끝내즈아!
#include <stdio.h>
#include <stdlib.h>
#include "BinarySearchTree.h"
int main(void)
{
BTreeNode * bstRoot;
BTreeNode * sNode; // search Node
BSTMakeAndInit(&bstRoot);
BSTInsert(&bstRoot, 5); BSTInsert(&bstRoot, 8);
BSTInsert(&bstRoot, 1); BSTInsert(&bstRoot, 6);
BSTInsert(&bstRoot, 4); BSTInsert(&bstRoot, 9);
BSTInsert(&bstRoot, 3); BSTInsert(&bstRoot, 2);
BSTInsert(&bstRoot, 7);
BSTShowAll(bstRoot); printf("\n");
sNode = BSTRemove(&bstRoot, 3);
free(sNode);
BSTShowAll(bstRoot); printf("\n");
sNode = BSTRemove(&bstRoot, 8);
free(sNode);
BSTShowAll(bstRoot); printf("\n");
sNode = BSTRemove(&bstRoot, 1);
free(sNode);
BSTShowAll(bstRoot); printf("\n");
sNode = BSTRemove(&bstRoot, 6);
free(sNode);
BSTShowAll(bstRoot); printf("\n");
return 0;
}
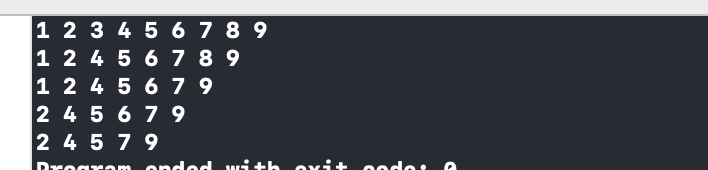
성공~
이로써 이진 탐색 트리에 대한이야기는 끝났지만....
탐색은 끝난것이아니와야..
다음 탐색에서 보쟈 ..
