[자료구조]우선순위 큐(Priority Queue)와 힙(Heap) 힙의 구현과 우선순위 큐의 완성 9-2-2

우선 좋은 모델은 아니나 이해하기 용이한 방식으로 힙을 구현한 후
보다 합리적인 형태로 변경하자 !

우선 헤더파일을 보자
SimpleHeap.h

//
//  SimpleHeap.h
//  Heap
//
//  Created by 서희찬 on 2021/04/11.
//

#ifndef SimpleHeap_h
#define SimpleHeap_h

#define TRUE 1
#define FALSE 0

#define HEAP_LEN 100

typedef char HData;
typedef int priority;

typedef struct _heapElem
{
    Priority pr; // 값이 작을수록 높은 우선순위
    HData data;
}HeapElem;

typedef struct _heap
{
    int numOfData;
    HeapElem heapArr[HEAP_LEN];
}Heap;

void HeapInit(Heap * ph);
int HIsEmpty(Heap * ph);

void HInsert(Heap * ph, HData data, Priority pr);
HData HDelete(Heap * ph);

#endif /* SimpleHeap_h */

위의 파일은 순수한 힙의 구현을 위한 헤더파일이라고 하기보다는 우선순위 큐의 구현을 염두에 두고 정의한 헤더파일이다.
이것은 구조체 정의에서 느낄 수 있다.

우선 순위 정보를 별도로 담을 수 있도록 정의한 pr을 보면 우선순위 큐의 구현을 고려했다는 것을 알 수 있다.

원리 이해 중심의 힙 구현 : HDelete 중심으로

이어서 헤더파일에 선언된 함수들의 정의를 보이기 앞서 다음 사실들을 정리하고 기억해야한다.

• 힙은 완전 이진 트리다.
• 힙의 구현은 배열을 기반으로하며 인덱스가 0인 요소는 비어둔다.
• 따라서 힙에 저장된 노드의 개수와 마지막 노드의 고유 번호는 일치한다.
• 노드의 고유번호가 노드가 저장되는 배열의 인덱스 값이 된다.
• 우선 순위를 나타내는 정수 값이 작을수록 높은 우선순위를 나타낸다고 가정한다.

이를 기반으로 코드를 짜보자 !
SimpleHeap.c

//
//  SimpleHeap.c
//  Heap
//
//  Created by 서희찬 on 2021/04/11.
//

#include "SimpleHeap.h"

void HeapInit(Heap * ph) // 힙의 초기화
{
   ph->numOfData = 0;
}

int HIsEmpty(Heap * ph) // 힙이 비었는지 체크
{
   if(ph->numOfData == 0)
       return TRUE;
   else
       return FALSE;
}

int GetParentIDX(int idx) // 부모 노드의 인덱스 값 반환
{
   return idx/2;
}

int GetLChildIDX(int idx) // 왼쪽 자식 노드의 인덱스 값 반환
{
   return idx*2;
}

int GetRChildIDX(int idx) // 오른쪽 자식 노드의 인덱스 값 반환
{
   return GetLChildIDX(idx)+1;
}

// 두 개의 자식 노드 중 높은 우선순위의 자식 노드 인덱스 값 반환
int GetHiPriChildIDX(Heap * ph, int idx)
{
   if(GetLChildIDX(idx)>ph->numOfData)
       return 0; //공집합 노드라는거 !
   else if(GetLChildIDX(idx)==ph->numOfData)
       return GetLChildIDX(idx); // 단말노드
   else
   {
       if(ph->heapArr[GetLChildIDX(idx)].pr>ph->heapArr[GetRChildIDX(idx)].pr)
           return GetRChildIDX(idx);
       else
           return GetLChildIDX(idx);
   }
}


// 힙에 데이터 저장
void HInsert(Heap * ph, HData data, priority pr)
{
   int idx = ph->numOfData+1;
   HeapElem nelem = {pr,data};
   
   while(idx!=1)
   {
       if(pr < (ph->heapArr[GetParentIDX(idx)].pr))
       {
           ph->heapArr[idx] = ph->heapArr[GetParentIDX(idx)];
           idx = GetParentIDX(idx);
       }
       else
          break;
   }
          ph -> heapArr[idx]= nelem;
          ph-> numOfData += 1;
}

// 힙에서 데이터 삭제
HData HDelete(Heap * ph)
{
   HData retData = (ph->heapArr[1]).data;
   HeapElem lastElem = ph->heapArr[ph->numOfData];
   
   int parentIdx = 1;
   int childIdx;
   
   while(childIdx = GetHiPriChildIDX(ph, parentIdx))
   {
       if(lastElem.pr <= ph->heapArr[childIdx].pr)
           break;
       ph->heapArr[parentIdx] = ph->heapArr[childIdx];
       parentIdx = childIdx;
       
   }
   ph->heapArr[parentIdx] = lastElem;
   ph->numOfData-=1;
   return retData;
}

헤더파일에 선언된 함수의 구현을 돕는 유용한 핢수들이 다수 정의되어 있는데 그 중 GetHiPriChildIDX 함수의 구현을 살펴보자 .

• idx값을 전달하면, 이 노드의 두 자식 중 우선순위가 높은 것의 인덱스 값을 반환한다.
• 자식 노드가 없으면 0, 자식 노드가 하나 인 경우에는 그 노드의 인덱스 값을 반환한다.

int GetHiPriChildIDX(Heap * ph, int idx)
{
// 자식노드가 없다면! 
    if(GetLChildIDX(idx)>ph->numOfData)
        return 0; 
// 자식 노드가 왼쪽 하나라면         
    else if(GetLChildIDX(idx)==ph->numOfData)
        return GetLChildIDX(idx); // 단말노드
 //자식 모두 존재
    else
    {// 오른쪽 자식 노드의 우선순위가 더 크다면
        if(ph->heapArr[GetLChildIDX(idx)].pr>ph->heapArr[GetRChildIDX(idx)].pr)
            return GetRChildIDX(idx);
        else
        // 왼쪽이 더 크다면 ! 
            return GetLChildIDX(idx);
    }
}

더 자세히보자 !

// 자식노드가 없다면! 
    if(GetLChildIDX(idx)>ph->numOfData)
        return 0; 

힙은 완전 이진트리이므로 오른쪽 자식 노드만 존재하는 상황은 발생 하지 않는다.
따라서 왼쪽 자식이 없다면 자식노드가 존재 하지 않는다는 것으로 판단 할 수 있다.

즉, 자식 노드가 하나도 존재하지않는 노드는 단말 노드이다.
그래서 단말 노드의 왼쪽 자식은 힙에 저장된 노드의 수를 넘어선다.
그러므로 위의 연산문으로 자식 노드의 유무를 체크할 수 있다.

// 자식 노드가 왼쪽 하나라면         
    else if(GetLChildIDX(idx)==ph->numOfData)
        return GetLChildIDX(idx); // 단말노드

하나뿐인 자식 노드는 왼쪽 자식 노드이다. 그리고 이것은 힙의 마지막 노드이다.
이 말을 보면 위의 코드가 완전 이해되지 않는가!?

이제 HDelete 함수를 보자.
그전에 우리는 다음과 같이 판단할 수있다.

"루트 노드로 올려진 마지막 노드는 자신의 위치를 찾을 때까지 아래로 이동하면서 자신의 위치를 찾아간다. 하지만, 이러한 빈번한 이동을 코드에 그대로 담을 필요는 없다. 최종 목적지가 결정되면 단번에 그리로 옮기면 된다.

// 힙에서 데이터 삭제
HData HDelete(Heap * ph)
{
    HData retData = (ph->heapArr[1]).data; //번환을 위해서 삭제할 데이터 저장
    HeapElem lastElem = ph->heapArr[ph->numOfData]; // 힙의 마지막 노드 저장
    
    // parentIdx 에는 마지막 노드가 저장될 위치정보가 담긴다.
    int parentIdx = 1; // 루트노드가 위치해야 할 인덱스 값 저장
    int childIdx;
    
    //루트 노드의 우선순위가 높은 자식 노드를 시작으로 반복문 시작
    while(childIdx = GetHiPriChildIDX(ph, parentIdx))
    {
        if(lastElem.pr <= ph->heapArr[childIdx].pr) // 마지막 노드와 우선순위 비교
            break; // 마지막 노드의 우선순위가 높다면 반복문 탈출 !
        // 마지막 노드보다 우선순위가 높으니, 비교대상 노드의 위츠를 한 레벨 올린다.
        ph->heapArr[parentIdx] = ph->heapArr[childIdx];
        parentIdx = childIdx; // 마지막 노드가 저장될 위치정보를 한 레벨 내림
        // 반복문 탈출하면 parentIdx에는 마지막 노드의 위치정보가 저장된다.
    }
    ph->heapArr[parentIdx] = lastElem; // 마지막 노드 최종 저장 
    ph->numOfData-=1;
    return retData;
}

마지막 노드가 있어야 할 위치를 parentIdx에 저장된 인덱스 값을 갱신해가며 찾아가고 있다.

HInsert 함수

삽입의 과정을 정리해보자

"새로운 데이터는 우선순위가 제일 낮다는 가정하에서 '마지막 위치'에 저장합니다. 그리고는 우선순위의 비교를 통해서 자신의 위치를 찾을 때까지 위로 올립니다."

// 힙에 데이터 저장
void HInsert(Heap * ph, HData data, priority pr)
{
    int idx = ph->numOfData+1; // 새 노드가 저장될 인덱스 값을 idx에 저장
    HeapElem nelem = {pr,data}; // 새 노드의 생성 및 초기화
    
    // 새 노드가 저장될 위치가 루트 노드의 위치가 아니라면 while문 반복
    while(idx!=1)
    {
        // 새 노드와 부모 노드의 우선순위 비교
        if(pr < (ph->heapArr[GetParentIDX(idx)].pr)) //새 노드의 우선순위가 더 높다면
        {
            // 부모 노드를 한 레벨 내린다.
            ph->heapArr[idx] = ph->heapArr[GetParentIDX(idx)];
            // 새 노드를 한 레벨 올린다.
            idx = GetParentIDX(idx);
        }
        else // 새 노드의 우선순위가 높지 않다면
           break;
    }
           ph -> heapArr[idx]= nelem; // 새 노드를 배열에 저장
           ph-> numOfData += 1;
}

Main 함수

//
//  main.c
//  Heap
//

#include <stdio.h>
#include "SimpleHeap.h"

int main(void)
{
    Heap heap;
    HeapInit(&heap);
    
    HInsert(&heap, 'A', 1);
    HInsert(&heap, 'B', 2);
    HInsert(&heap, 'C', 3);
    printf("%c \n", HDelete(&heap));
    
    HInsert(&heap, 'A', 1);
    HInsert(&heap, 'B', 2);
    HInsert(&heap, 'C', 3);
    printf("%c \n",HDelete(&heap));
    
    while(!HIsEmpty(&heap))
        printf("%c \n", HDelete(&heap));
    
    return 0;
}

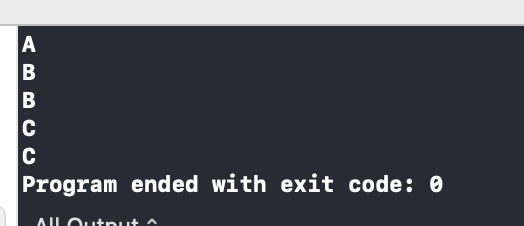
실행결과 우선순위가 높은 문자들이 먼저 꺼내졌음을 증명하고 있다.

우리가 구현한 위의 힙은 좋은 평가를 받을 만한 수준 일까?

우리가 구현한 힙이 딱 어울릴만한 상황에서는 좋은 평가를 기대할수도 있다. 하지만 일반적인 상황에서도 좋은 평가를 기대하기에는 몇 가지 부족한 점이 존재한다.
이는 구조체의 정의에서 우선 발견할 수 있다.

typedef struct _heapElem
{
    Priority pr; // 값이 작을수록 높은 우선순위
    HData data;
}HeapElem;

위의 구조체 맴버로 우선순위 정보를 담는 변수가 선언되어있다.
이것이 문제로 지적될 수 있는 부분이다.
또 다른 부분은

void HInsert(Heap * ph, HData data, Priority pr);
// 우선순위 정보도 넘겨라

이는

데이터를 입력하기 전에 너희가 알아서 우선순위를 결정하고 그 값을 전달해줘야 해 ! 이다.

그러면 우리는 다음과 같이 항변해야한다.

"우선순위라는 것이 데이터를 기즌으로 결정되는 경우가 대부분인데... 우선순위의 결정 기준을 알려달라는 것도 아니고.. 우선순위를 직접 결정해서 알려달라고..?\그것도 숫자로..? 장난해 임마...?

이러한 불만을 근본적으로 해결하기위해서 힙을 변경해보자.