힙의 구현은 곧 우선순위 큐의 완성으로 이어진다고해서
이 둘이 동일하다는것은 정확하지 않는것이다.
그러므로 구분할 수 있어야한다.
힙은 우선순위 큐의 구현에 어울리는, 완전 이진 트리의 일종이라는 사실을 기억해야한다.
힙에서의 데이터 저장과정
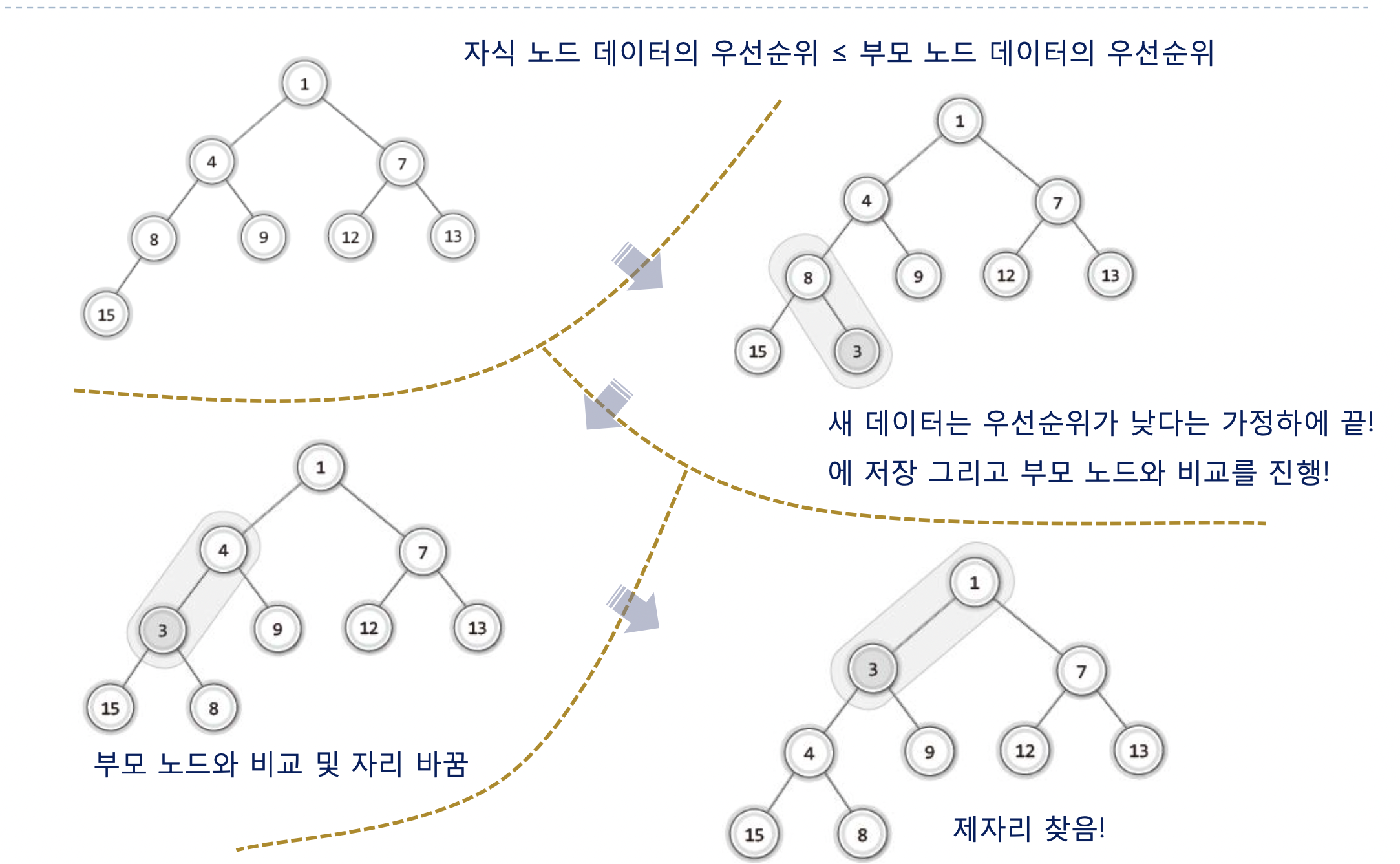
"마지막 위치"는 노드를 추가한 이후에도 완전 이진트리가 유지되는 !
힙에서의 데이터 삭제과정
힙에서 루트 노드를 어떻게 삭제하는 가는 쉽지만 이 후에도 힙의 구조를 유지해야 하므로
" 힙에서 루트 노드 삭제후 다음에 이부분을 어떻게 채울까? 라고 생각해봤지만..
해결책은 간단하다.
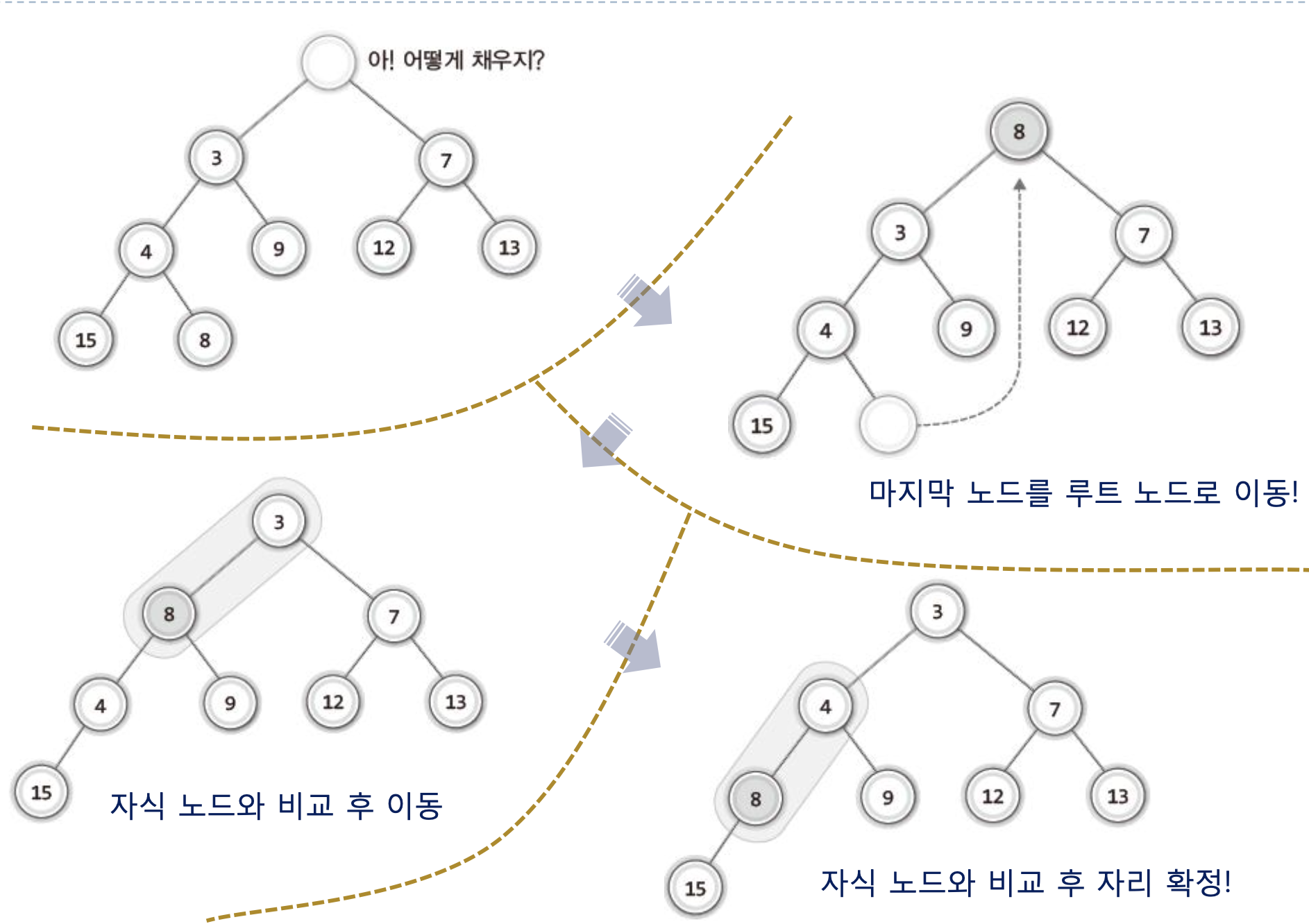
참고로 우선순위가 낮은 자식 노드와 교환하면 안 되는 이유는 힙의 기본 조건이 무너지는 것을 방지하기 위해서이다.
삽입과 삭제의 과정에서 보인 성능의 평가
우선순위 큐의구현에 있어서 단순 배열이나 연결 리스트보다 힙이 더적합한 이유는 어디에 있는가?
여기에 대한 답을 시간 복잡도로 보자.
배열 기반
저장의 시간 복잡도 O(n) : 저장된 모든 데이터와 우선순위 비교 과정을 거쳐야하기 때문
삭제의 시간 복잡도 O(1) : 맨 앞 데이터 삭제 하면 된다.
연결리스트 기반
저장의 시간 복잡도 O(n) : 저장된 모든 데이터와 우선순위 비교 과정을 거쳐야하기 때문
삭제의 시간 복잡도 O(1) : 맨 앞 데이터 삭제 하면 된다.
이와 같이 배열/연결리스트 기바의 경우는 다를 바 없다.
하지만.. 힙의 경우는 어떤가?
삽입이나 삭제의 경우 동반되는 비교연산은 주로 부모 노드와 자식 노드 사이에서 일어난다.
그리고 이것이 의미하는 바는 다음과 같다
"힙을 기반으로 하면 틑르이 높이에 해당하는 수만큼만 비교연산을 진행하면 됩니다."
이는 트리의 높이가 하나 늘면 비교연산도 하나 증가한다는 뜻이므로
힙 기반
저장 시간 복잡도 : log 이 엔
삭제 시간 복잡도: 로그 이 엔 !
힙은 완전 이진트리이므로 저장 할 수 있는 데이터의 수는 높이가 하나 늘때마다 두 배씩 증가한다.
그러므로 !
데이터의 수가 두 배 늘 때마다, 비교연산의 횟수는 1회 증가한다.
그러므로 빅오를 비교해봤을때 힙이 매우 큰 성능의 우월성을 가지고 있다는것을 확인할 수 있다.
힙의 구현에 어울리는 것은 연결리스트? 배열?
우선 순위 큐의 구현에 어울리는 것은 힙이라는 것을 배웠다.
그렇다면 ! 이제 이 힙의 구현방법에 대해 고민해야 한다.
힙은 트리다..
트리 망할 트리.. 다시 나왔다..
앞서 트리를 구현할 때 연결리스트를 사용했지만..완전 이진트리 구조를 가질때 배열을 이용하다고 말했던게 기억나는가?
그렇다!
힙을 구현할때는 배열을 이용한다.
그 이유는
연결 리스트를 기반으로 힙을 구현하면, 새로운 노드를 힙의 "마지막 위치"에 추가하는 것이 쉽지 않다.
그래서 힙과 같이, 새로운 노드를 추가한 이후에도 완전 이진 트리를 유지해야 하는 경우에는 연결 리스트가 아닌 배열을 기반으로 트리를 구현해야 한다.
배열을 기반으로 힙을 구현하는데 필요한 지식

구현의 편의를 위해서 인덱스가 0인 위치를 사용하지 않는것은 앞서 말한 바 있다.
그렇다면 배열 기반으로 힙을 구현하기 위해서는 무엇을 알아야할까..?
"왼쪽 그리고 오른쪽 자식노드의 인덱스 값, 부모노드의 인덱스값"
어떻게 구하지... 생각을 해보자
그림의 배열 인덱스 값을 자세히보자!!
그렇다!
- 왼쪽 자식 노드의 인덱스 값 : 부모 노드의 인덱스 값 *2
- 오른쪽 : 부모 노드 인덱스 값*2 +1
- 부모 노드의 인덱스 값 :
자식노드의 인덱스 값 /2(정수형 나눗셈)
이제 다음 페이지에서 원리 이해 중심으로 힙을 구현해보자.
