int Partition(int arr[],int left, int right)
{
int pivot = arr[left]; // pivot is most left
int low = left+1;
int high = right;
printf("피벗 : %d \n",pivot); // 피벗의 확인을 위해서 추가할 문장printf 를 추가해주면 선택된 피벗이 무엇인지, 정렬과정에서 몇 개의 피벗이 선택되었는지 확인할 수 있다.
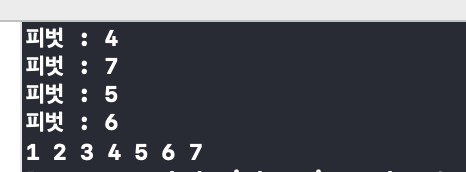
이와 같이 !
선택된 피벗의 수는 정렬의 효율을 가늠하는 기준이 된다.
그럼 다음 배열로 설정해보자 .
int arr[15] = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15};
윽.. 돌리기전부터 최악의 상황이란게 보인다.
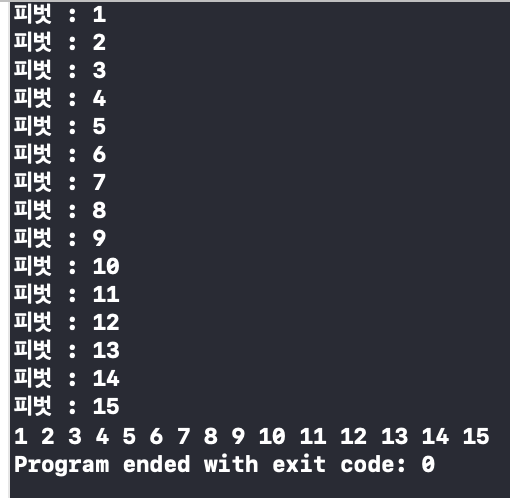
우와.. 총 15개의 피벗이 선택되었다,,
ㄹㅇ 최악이다.
따라서 우리는 최악의 상황을 면하기 위해서 피벗의 선택방법을 다음과 같이 바꾸자
"정렬대상의 가장 왼쪽, 가장 오른쪽, 그리고 중간에 위치한 값을 추출해서 이 중에서 중간에 해당하는 값을 피벗으로 결정한다."
어디서 많이 본거같지 않는가!
바로 앞선 포스터에서 보여준 "중간 값 고르기"에 해당한다.
이제 이렇게 피벗이 결정되도록 예제를 변경해보자!
그래서 위의 배열을 대상으로 정렬을 진행했을 때 선택 되는 피벗의 수를 확인해보자.
답
#include <stdio.h>
void Swap(int arr[],int idx1, int idx2)
{
int temp = arr[idx1];
arr[idx1] = arr[idx2];
arr[idx2] = temp;
}
int MedianOfThree(int arr[],int left,int right)
{
int samples[3] = {left,(left+right)/2,right}; //values is index
if(arr[samples[0]]>arr[samples[1]])
Swap(samples,0,1);
if(arr[samples[1]] > arr[samples[2]])
Swap(samples, 1, 2);
if(arr[samples[0]]>arr[samples[1]])
Swap(samples, 0, 1);
return samples[1];
}
int Partition(int arr[],int left, int right)
{
int pIdx = MedianOfThree(arr, left, right); // pivot is most left
int pivot = arr[pIdx];
int low = left+1;
int high = right;
Swap(arr, left, pIdx); // 피벗을 가장 왼쪽으로 이동
printf("피벗 : %d \n",pivot); // 피벗의 확인을 위해서 추가할 문장
//교차되기전까지 반복
while(low <= high)
{
// find higher than pivot
while(pivot >= arr[low] && low<= right)
low++; // low going right
// find lower than pivot
while(pivot<=arr[high] && high >= (left+1))
high --;
//교차 되지 않았을때 서로 교환
if(low<=high)
Swap(arr,low,high);
}
Swap(arr,left,high); // 피벗과 하이가 가리키는 대상 교환
return high; // 옮겨진 피벗의 위치정보 반환.
}
void QuickSort(int arr[],int left, int right)
{
if(left<=right)
{
int pivot = Partition(arr, left, right);
QuickSort(arr, left, pivot-1);
QuickSort(arr, pivot+1, right);
}
}
int main(void)
{
int arr[15] = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15};
// int arr[3] = {;
int len = sizeof(arr)/sizeof(int);
int i;
QuickSort(arr, 0, len-1); //arr에 대해서 퀵 정렬 진행 시작 !
for(i=0;i<len;i++)
{
printf("%d ",arr[i]);
}
printf("\n");
return 0;
}
int MedianOfThree(int arr[],int left,int right)
{
int samples[3] = {left,(left+right)/2,right}; //values is index
if(arr[samples[0]]>arr[samples[1]])
Swap(samples,0,1);
if(arr[samples[1]] > arr[samples[2]])
Swap(samples, 1, 2);
if(arr[samples[0]]>arr[samples[1]])
Swap(samples, 0, 1);
return samples[1];
}
중간 값을 갖는 요소의 인덱스 값을 반환하는 함수를 짠다.
if문을 사용하여 버블정렬을 이용하여 중간 값을 구했다.
이렇듯 하나의 알고리즘을 짜는데 다른 알고리즘은 성능을 구현하는데 도움이 될 수 있다.
이제 나머지 코드를 수정해주자
"피벗을 선택했다면, 이를 가장 왼쪽에 있는 데이터와 교환한다.
왜 이런지 아겠는가!?
우리가 구현해놓은 코드를 최대한 수정하지 않기위해서이다.
우리가 구현한 코드는 피벗이 가장 왼쪽에 위치하는 상황에서 동작한다.
따라서 Swap(arr,left,pIdx)를 통해 서로 바꿔준다!
이렇게하면 선택되는 피벗의 수가 반으로 줄어든다!
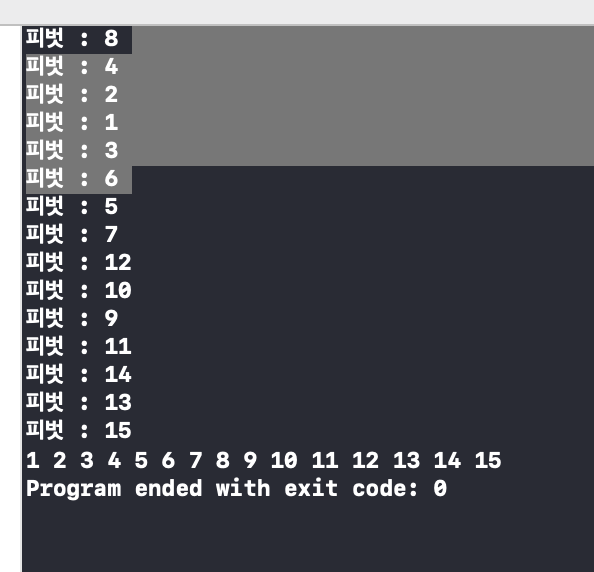
음.. 그대로인데.. ㅋ?
부록
문제를 풀었는데 되게 복잡? 난잡하게 접근했다.
처음에는 MOT를 정의하고나서 left,right받는것을 다 생각했다가 결국 배열만 받고 배열안에서 첫,중간,마지막 값을 int로 초기화 시킨후 이들을 비교연산 진행하는데
if문이 무진장 많아졌다.
하지만!
이는 버블정렬을 이용하고 미리 정의한 Swap함수를 이용하면 매우 간결하게 해결된다는것에 놀라움을 금치 못했다!
그리고 우리가 구현한 코드에서의 left와 pIdx값을 변경하는것도 생각하지 못했다.
그저.. 내가 most 중간값을 넣어주면
알아서 Partition이 진행될줄 알았는데
생각해보니 밑에 짜여진 함수들은 모두 left가 pivot이라는 가정하에 짜여진 함수 들이였다.
그러므로 Swap(arr,left,pIdx)!
이렇게 Swap을 자유자재로 이용할줄알아야한다는 것을 배울 수 있어서 되게 좋다!
윤성우선생님 감사합니다 !
