기수 정렬 : 이해 1
퀵 정렬까지 알고 나면 그 나름의 만족감에 더 이상의 정렬 알고리즘에는 관심이 가지 않는 다는 말이 많다!
하지만! 기수 정렬 알고리즘은 다음과 같은 특징이 있다.
"정렬 순서상 앞서고 뒤섬의 판단을 위한 비교연산을 하지 않는다."
비교연산은 정렬 알고리즘의 핵심이다.
특히! 두 데이터 간의 우선순위를 판단하기 위한 비교연산은 핵심중의 핵심이였다!
따라서 앞선 모든 알고리즘들은 이 연산을 포함하고 있었고 알고리즘의 복잡도 또한 이 연산을 근거로 판단했다.
그런데 ! 이런 유형의 연산을 하지 않고 정렬 할수 있다니! 흥미롭지 않은가!

정렬알고리즘의 이론상 성능의 한계는 O(log(2)n)인데 기수정렬은 이러한 한계를 넘어설 수 있는 유일한 알고리즘이다.
물론 단점 또한 존재한다.
바로 "데이터의 길이"에 따라 제한적으로 적용 가능하다는 것이다.
길이가 같은 데이터들을 대상으로 정렬이 가능하지만, 같지 않은 데이터들을 대상으로는 정렬이 불가능하다.
-999 이상 999 이하의 값들도 기수 정렬의 대상이 될 수 있지만!!!
이를 위해서 별도의 알고리즘을 고민해야하고 이 알고리즘 적용으로 인한 효율의 문제 또한 고미해야한다!
그런데..
이렇게 까지하면서 기수 정렬을 사용할 이유가 있겠는가!
이제 서론을 끝내고 기수정렬의 원리에 대해 배워보자!
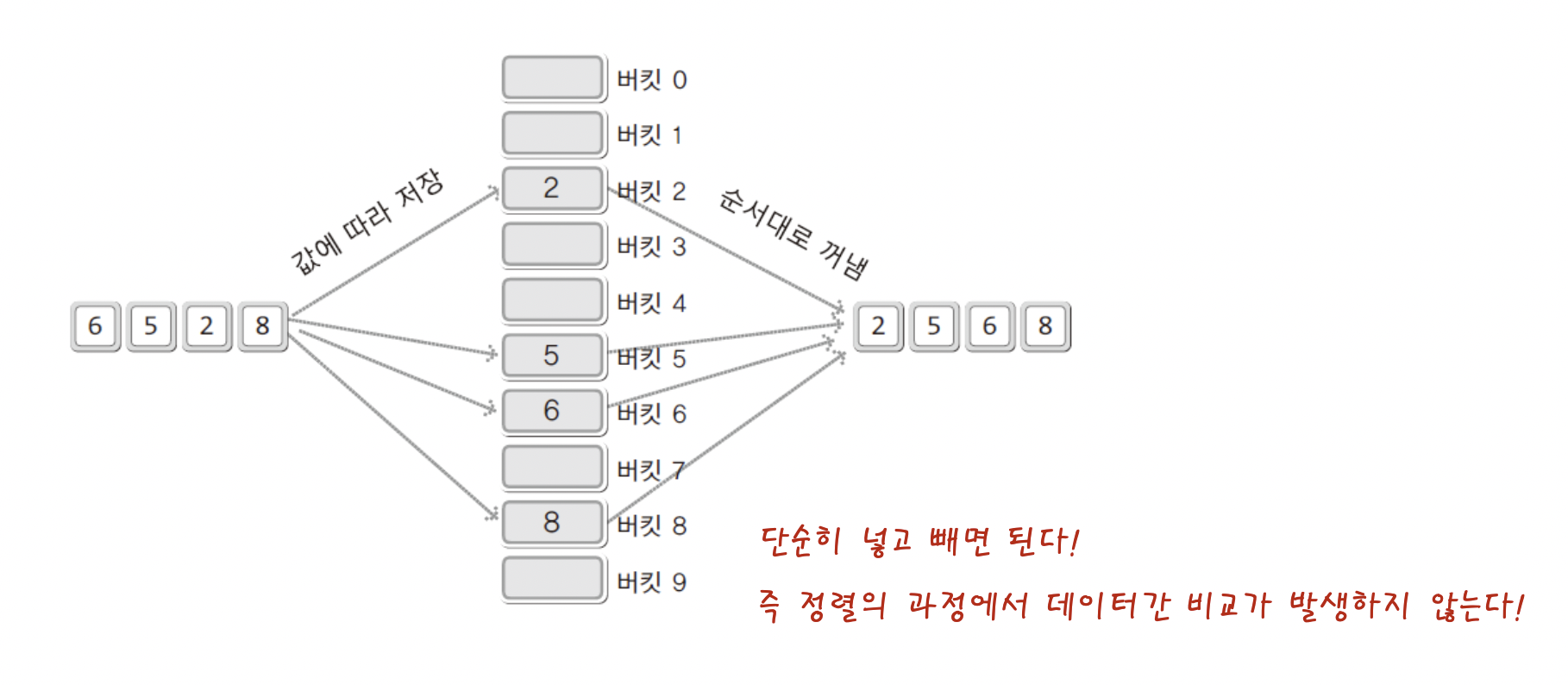
그림을 보고 생각해보자!
위 그림에서는 10진수 정수의 정렬과정을 보여주고 있다.
그리고 이 정수의 정렬을 위해서는 총 열개의 양동이가 필요하고 이는 각각 순서대로 이름이 매겨져 있다.
그리고 정렬대상은 값에 해당하는 버킷으로 이동 후 양동이에서 순서대로 꺼내면!
정렬 완료이다!!
이것이 기수 정렬의 기본이해이다.
보다 진지한이야기에 들어가기 앞서
"기수(radix)"란 주어진 데이터를 구성하는 기본 요소를 의미한다.
예를 들어 2진수는 0 과 1
10진수는 0부터 9까지이다.
그런데! 위 그림에서는 기수의 개수만큼 버킷을 마련해서 정렬을 진행하지 않는가! 따라서 우리는 기수정렬을 다음과 같이 정의할 수 있다.
"데이터를 구성하는 기본 요소, 즉 기수를 이용해서 정렬을 진행하는 방식"
이렇듯 기수 정렬은 기수를 이용한 정렬 방식이기에 세 자릿수 다섯 자릿수를 정렬한다해도! 10진수 정수라면 버킷은 기수의 개수인 열 개가 필요하다!
그럼.. 이제 다시 생각해보자
영단어를 정렬 해야 한다면..?
그것도 특수 문자를 포함하는 영단어라면...
총 몇개의 양동이가 필요하겠는가..
이를 통해 단점을 간단하게나마 이해할 수 있을것이다.
기수 정렬 : 이해 2
보다 깊은 이해를 위해서 세 자릿수 정수들을 대상으로한 기수 정렬을 보이겠다.
오름차순이고 이들은 5진수로 표현되었다!
그렇다면 5개의 양동이만을 가지고 기수 정렬의 과정을 보일 수 있다.
134, 224, 232 , 122
이는
LSD 기수 정렬
이라고 한다.
LSD(Least Significant Digit)으로 덜 중요한 자릿수에서부터 정렬을 진행해 나간다는 의미를 담고 있다.
즉! 첫번째 자릿수부터 시작해서 정렬을 진행해 나간다는 의미이다.
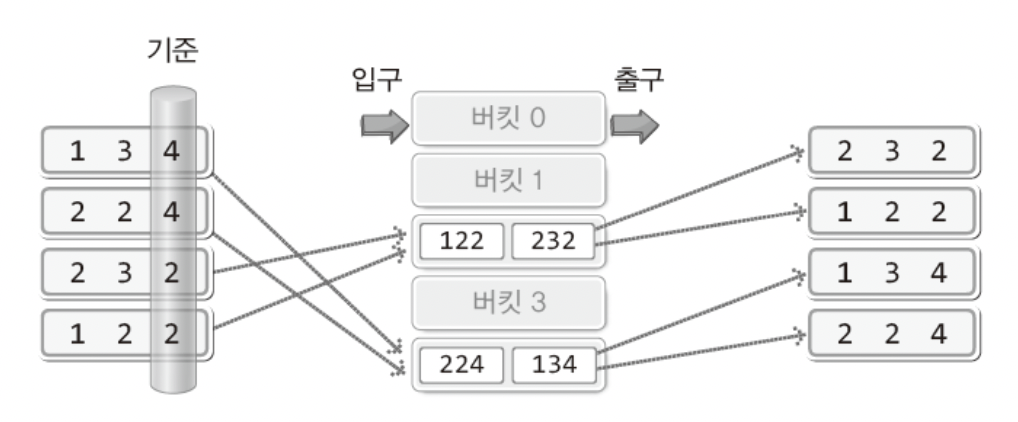
우선 첫번째 자리부터 순서대로 넣어준다!
버킷에 두개 다 넣고 꺼낼때는 먼저 들어간 순서대로 꺼내면 된다!
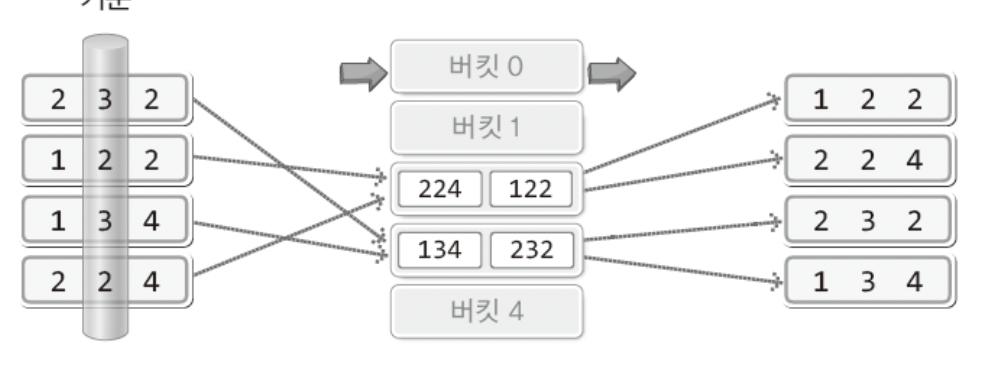
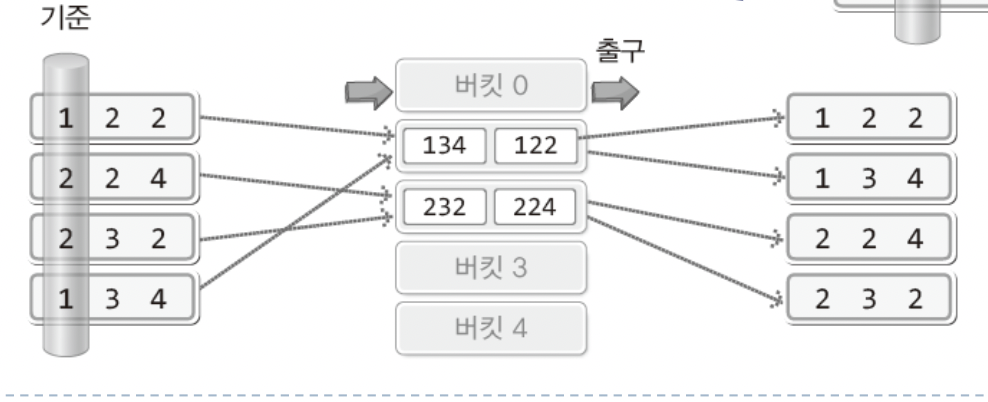
이후 두번째,세번째 자리까지 동일한 방식으로 진행하고 나면 정렬이 완료되었다!!
이 방법은 간단하긴 하지만 익숙하지는 않다!
왜냐하면 우리는 가장 큰 자릿수부터 비교해서 대소를 판단하는데 익숙한데 비해 이 방법은 첫번째 자릿수부터 비교해서 정렬이 끝나기 전까지 대소를 판단하는것이 불가능하다는 점도 있다.
이것이 단점인데 이러한 담점은 프로그래밍하는데 있어서는 장점이 된다!
다음 포스트에서는 LSD vs MSD 를 비교해보자 !
