트리는 계층적 관계를 "표현"하는 자료구조이다.
트리를 통해서 무엇인가를 저장한다는 생각보다 "표현" 한다고 생각하는 것이 좋다.
"데이터의 저장, 검색 및 삭제가 용의하게 정의 되어있나여?"
보다는
"트리의 구조로 이뤄진 무엇인가를 표현하기에 적절히 정의되어 있나요?" 라는 시야가 필요하다.
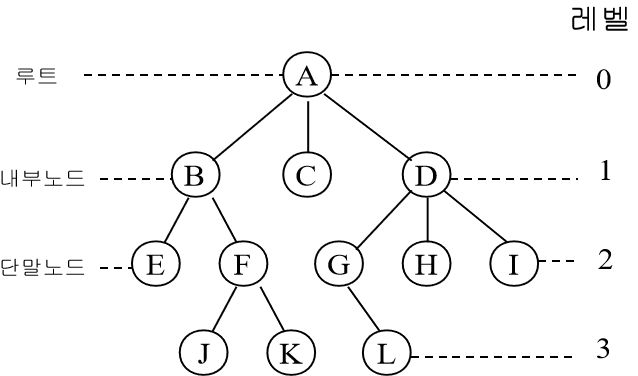
트리는 이르케 생겼고
트리를 관련 용어를 소개하겠다.
-
노드 : node
트리의 구성요소에 해당 -
간선 : edge
노드와 노드를 연결하는 연결선 -
루트노드 : root node
트리 구조에서 최상위에 존재하는 A와 같은 노드 -
단말 노드 : terminal node
아래로 또 다른 노드가 연결되어 있지 않은 노드 -
내부 노드 : internal node
단말 노드를 제외한 모든 노드로 A,B와 같은 노드
이진트리와 서브 트리

서브트리는 이렇게 큰 트리에 속하는 작은 트리를 가리켜 서브트리 라고한다.
그런데 이러한 서브 트리들이 모여서 큰 트리를 이룬다는 표현이 가끔 있는데..
이는 잘못된 표현이다.
서브트리는 큰 트리 안에 종속된 관계이기에 아무리 모여도 큰 트리를 이루지 못한다.
이로써 서브트리를 설명했으니
이진 트리를 보여주겠다.
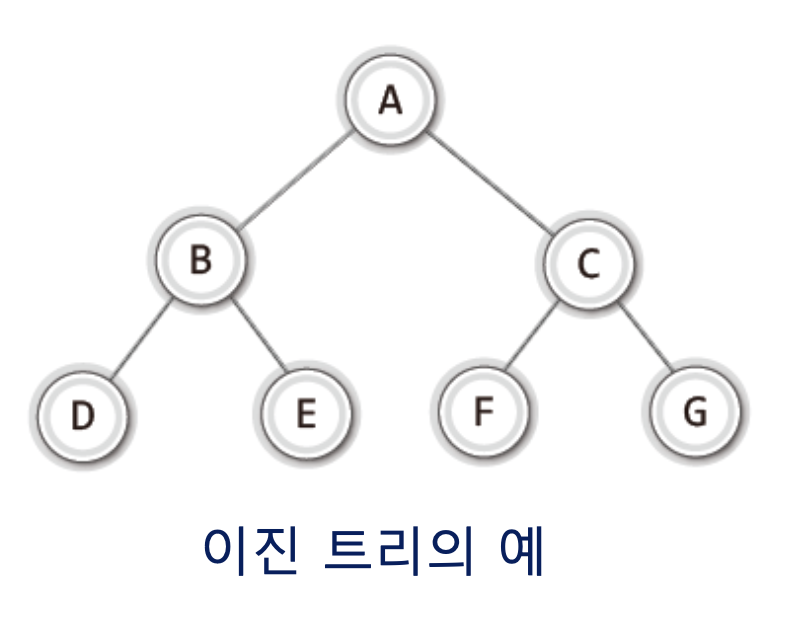
이러한 이진 트리는 다음 두 조건을 만족해야한다.
- 루트 노드를 중심으로 두 개의 서브 트리로 나뉘어진다.
- 나뉘어진 두 서브 트리도 모두 이진 트리이어야한다.
이것이 온전한 이진트리의 정의 이다.
이러한 이진 트리는 조건 자체가 재귀적이기 때문에 이렇게 정의할 수밖에 없다.
이것을 조금 쉽게 설명 할 수 있지만 이는 재귀적인 조건을 완전히 담지 못한 설명이다
"이진 트리가 되려면, 루트 노드를 중심을 둘로 나뉘는 두 개의 서브 트리도 이진트리어야 하고, 그 서브 트리의 모든 서브 트리도 이진 트리이어야 한다"
그런데..
이진 트리 조건이 여기까지라면 다음 같은 트리를 보고 의문이 들 수 있다.

이르케 비어있는것도 이진트리인데
그이유는 오른쪽 사진 처럼 없는 곳은 공집합노드라고 생각하기 때문이다.
즉, 이진트리가 되지 않는 조건은 노드가 2개를 초과하면 이진트리 ㅃㅇ!!! 이고 그 외에는 1개나 0개가 있을때는 공집합 노드로 남은 부분들을 채운다고 생각 하면된다 !

이러한 이진트리를 좀 더 세분화 할 수 있다.
위와 같이 완전히 꽉 ~ 찬 포화 이진트리와
빈 틈 없이 차곡차곡 채워진 ! 그런데 이 채워진 기준이
왼쪽 기준으로 채워져야한다!!!
그게 좀 더 안정적인거 같지않은가!!? ㅋㅅㅋ
쨌든 왼쪽이 비어져 있고 오른쪽부터 채워진 이진트리는 Just 그냥 이진 트리이다.
이제 이진트리에 대해 간단한 설명이 끝났으니
이진 트리의 구현에 대해 시작하겠다 !
