[자료구조]Tree - (8-2)

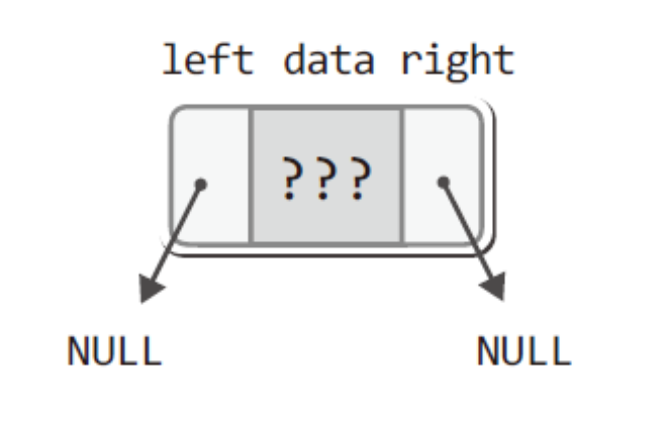
이진트리의 구현 방법 또한
배열기반과 연결리스트 기반이 있다.

<배열 기반>

<연결리스트 기반>

대체적으로 연결리스트 기반으로 하는 방식이 더 유연하지만 "완전 이진트리" (트리가 완성된 이후로는 그 트리로는 매우 빈번한 탐색이 이뤄진다)같은 경우라면 배열 기반이 연결 리스트에 비해서 탐색이 매우 용이하고 빠르기 때문에 배열기반의 이진트리를 생각 해보는 것도 좋다 !

이진 트리는 ADT 정의 전에 헷갈릴 수 도있으니 먼저 헤더 파일을 보고 가자 !

노드에 데이터가 이러한 형식으로 저장된다고 시각적으로 보고 가면 더 이해가 잘 될것이다.

BinaryTree.h

//
//  BinaryTree.h
//  BinaryTree

#ifndef BinaryTree_h
#define BinaryTree_h

typedef int BTData;

typedef struct _bTreeNode // 이진 트리의 노드를 표현한 구조체이다.
{
    BTData data; // 가지고 있는 데이터
    struct _bTreeNode * left; // 왼쪽 빈칸
    struct _bTreeNode * right; // 오른쪽 빈칸
} BTreeNode; // 타입뎊!

BTreeNode * MakeBTreeNode(void); // 노드의 생성
BTData GetData(BTreeNode * bt); // 노드에 저장된 데이터 반환
void SetData(BTreeNode * bt, BTdata data); // 노드에 데이터 저장

BTreeNode * GetLeftSubTree(BTreeNode * bt); // 왼쪽 서브 트리 주소 값 반환
BTreeNode * GetRightSubTree(BTreeNode * bt); // 오른쪽 서브 트리 주소 값 반환

void MakeLeftSubTree(BTreeNode * main, BTreeNode * sub); //Main노드가 왼쪽 자식 노드로 sub노드 연결
void MakeRightSubTree(BTreeNode * main, BTreeNode * sub); //Main노드가 오른쪽 자식 노드로 sub노드 연결

#endif /* BinaryTree_h */

Q. 노드 A,B,C를 생성해서 A를 루트로 하고, B C 를 각 각 왼쪽 오른쪽 자식 노드가 되도록 구성하기 위해서는 함수의 호출 흐름을 어떻게 가져야하는가 ?
A.

int main(void)
{
    BTreeNode * ndA = MakeBTreeNode(); // node A 생성
    BTreeNode * ndB = MakeBTreeNode(); // node B 생성
    BTreeNode * ndC = MakeBTreeNode(); // node C 생성
    ....
    MakeLeftSubTree(ndA,ndB); //노드 A의 왼쪽 자식 노드로 노드 B 연결
    makeRightSubTree(ndA,ndC);//노드 A의 오른쪽 자식 노드로 노드 C 연결   
}

-> 왼쪽 자식 노드를 추가하는 과정과 왼쪽 서브트리를 추가하는 과정은 똑같다 !!@!

이를 통해서 이진 트리의 자료구조의 ADT를 소개하겠다.

BTreeNode * MakeBTreeNode(void);
- 이진 트리 노드를 생성하여 그 주소 값을 반환한다. 

BTData GetData(BTreeNode * bt);
- 노드에 저장된 데이터 반환

void SetData(BTreeNode * bt, BTData data);
- 노드에 데이터 저장, data로 전달된 값을 저장한다.

BTreeNode * GetLeftSubTree(BTreeNode * bt);
- 왼쪽 서브 트리의 주소 값 반환

BTreeNode * GetRightSubTree(BTreeNode * bt);
-오른쪽 서브 트리의 주소 값 반환

void MakeLeftSubTree(BTreeNode * main, BTreeNode * sub);
- 왼쪽 서브 트리를 연결한다.

void MakeRightSubTree(BTreeNode * main, BTreeNode * sub);
- 오른쪽 서브 트리를 연결한다. 

이제 이를 통해 이진 트리를 구현해보자.

//
//  BinaryTree.c
//  BinaryTree
//
#include <stdio.h>
#include <stdlib.h>
#include "BinaryTree.h"

BTreeNode * MakeBTreeNode(void)
{
    BTreeNode * nd = (BTreeNode *)malloc(sizeof(BTreeNode)); //nd 노드 동적할당
    nd->left = NULL;
    nd ->right = NULL; //왼쪽 오른쪽 Null 가리키게한다.
    return nd;
}

BTData GetData(BTreeNode * bt)
{
    return bt->data; //bt에 저장된 data 값을 반환해서 보여준다
}

void SetData(BTreeNode * bt, BTData data)
{
    bt->data = data; //bt의 data값을 전달받은 data로 넣는다.
}

BTreeNode * GetLeftSubTree(BTreeNode * bt)
{
    return bt->left; // 왼쪽 서브 트리 주소 값 반환
}

BTreeNode * GetRighttSubTree(BTreeNode * bt)
{
    return bt->right;
}

void MakeLeftSubTree(BTreeNode * main, BTreeNode * sub)
{
    if(main->left != NULL)
        free(main->left); // 만약 main의 left가 이미 차져있다면 그 쪽 데이터를 지운다 !
    
    main->left = sub; // sub로 넣는다 !
}

void MakeRightSubTree(BTreeNode * main, BTreeNode * sub)
{
    if(main->right != NULL)
        free(main->right); // 만약 main의 left가 이미 차져있다면 그 쪽 데이터를 지운다 !
    
    main->right = sub; // sub로 넣는다 !
}

생각외로... 매우 간단하다..
역시 생각하고 이해하는것이 매우 힘들고 코드짜는게 매우 어려운것이 자료구조 인가..!?

여기서 간단하게 언급할만한 함수는 MakeLeftSubTree/Right 인데 그 이유는 이미 왼/오에 서브트리가 존재한다면 해당 서브트리를 삭제하고 새로운 트리를 연결하는 것인데...!

여기에는 치명적인 문제가 있다.

"한 번의 free 함수 호출이 전부이기 떄문에, 삭제할 서브 트리가 하나의 노드로 이뤄져 있다면 문제되지 않지만, 그렇지 않다면 메모리의 누수로 이어진다"

둘 이상의 노드로 이뤄져 있는 서브트리를 완전히 삭제하기 위해서는 모든 노드를 대상으로 free 함수를 호출 해야한다.
이렇게 모든 노드를 방문하는것을 "순회"라고한다.
순회는 이제 추후에 설명하겠다.

이제 이 이진트리 코드의 메인코드를 보겠다.

//
//  main.c
//  BinaryTree
//
//  Created by 서희찬 on 2021/04/06.
//

#include <stdio.h>
#include "BinaryTree.h"

int main(void)
{
    BTreeNode * bt1 = MakeBTreeNode(); // 노드 1 생성
    BTreeNode * bt2 = MakeBTreeNode(); // 노드 2 생성
    BTreeNode * bt3 = MakeBTreeNode(); // 노드 3 생성
    BTreeNode * bt4 = MakeBTreeNode(); // 노드 4 생성
    
    SetData(bt1, 1); //bt1 에 1 저장
    SetData(bt2, 2); //bt2 에 2 저장
    SetData(bt3, 3); //bt3 에 3 저장
    SetData(bt4, 4); //bt4 에 4 저장
    
    MakeLeftSubTree(bt1, bt2); // bt2를 bt1의 왼쪽 자식 노드로
    MakeRightSubTree(bt1, bt3); // bt3를 bt1의 오른쪽 자식 노드로
    MakeLeftSubTree(bt2, bt4); // bt4를 bt2의 왼쪽 자식 노드로
    
    // bt1 의 왼쪽자식 노드의 데이터 출력
    printf("%d \n", GetData(GetLeftSubTree(bt1)));
    
    // bt 1의 왼쪽 자식 노드의 왼쪽 자식 노드 데이터 출력
    printf("%d \n",GetData(GetLeftSubTree(GetLeftSubTree(bt1))));
    
    return 0;
}

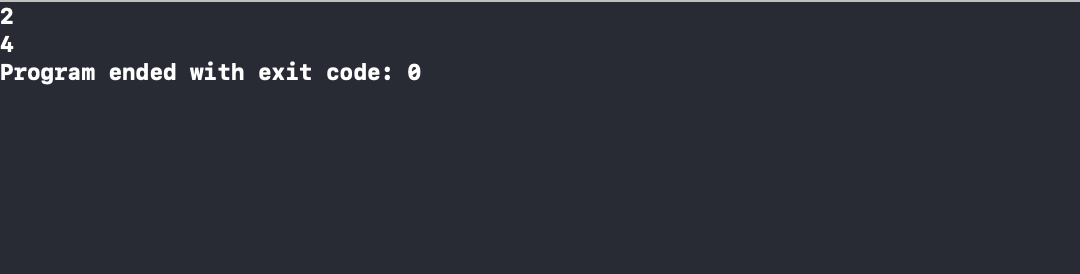
성공 ~
이제 다음은 순회에 대해 공부해보자 !