드디어 마지막 챕터이다..
그래프만 끝내고 이제 쉬자!!!!!는 개뿔....
c++/알고리즘문제/java 가 남아있다..
ㅇㅁㅇ 집인데 집가고싶당.....
그럼 마지막 챕터 그래프를 시작하겠다.
그래프의 역사와 이야깃거리
그래프 알고리즘은 수학자 '오일러'에 의해 고안됬다.
오일러는 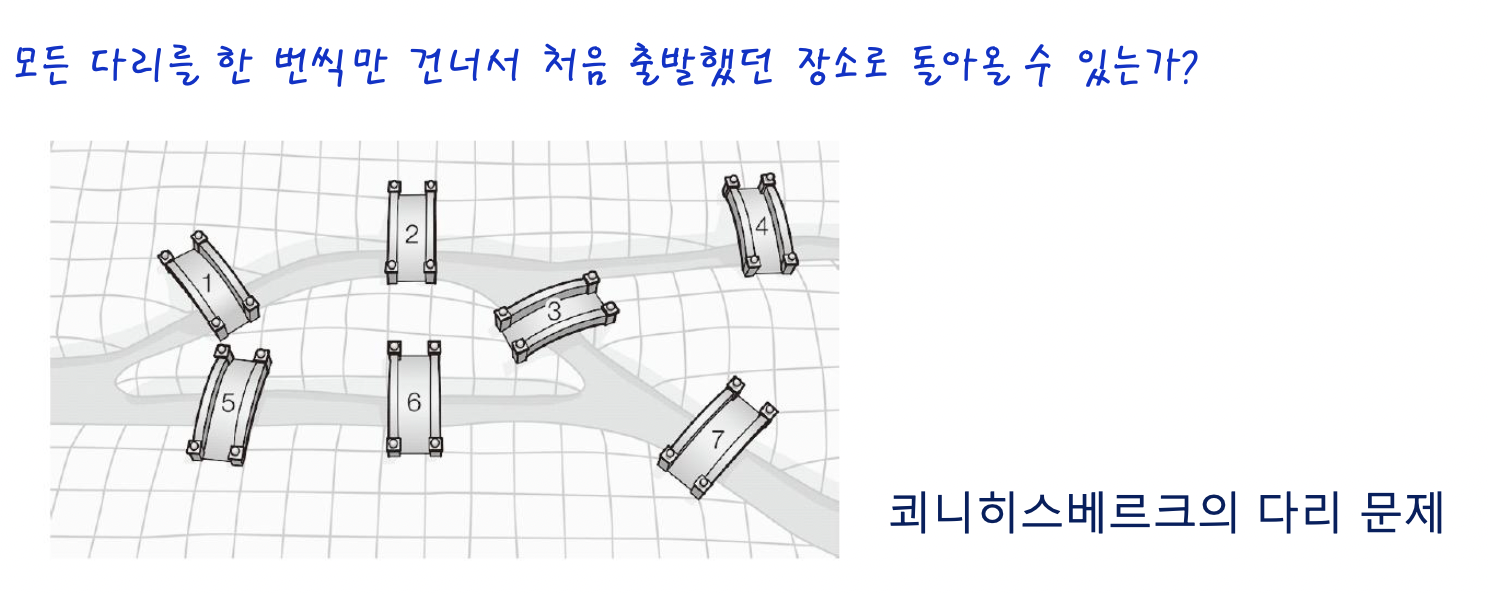
이 문제를 해결하기 위해서 그래프 이론을 사용하였다고 한다!
이렇듯 그래프 이론은 오래되었고 이것이 컴퓨터 분야에서 알고리즘으로 활용되기 시작한지는 얼마 되지 않았다.
그럼! 저 다리 문제가 뭔지 보자 한번!!!
저 문제를 해결하는것은 한두번 해보면 불가능하다는것을 깨달을것이다.
이 문제가 가능하기 위해서는
"정점 별로 연결된 간선의 수가 모두 짝수이어야, 간선을 한 번씩만 지나서 처음 출발했던 정점으로 돌아올 수 있다."
라는 필요충분 조건을 만족시켜야한다.
그런데 정점이랑 간선이 무엇인지 알겠는가?
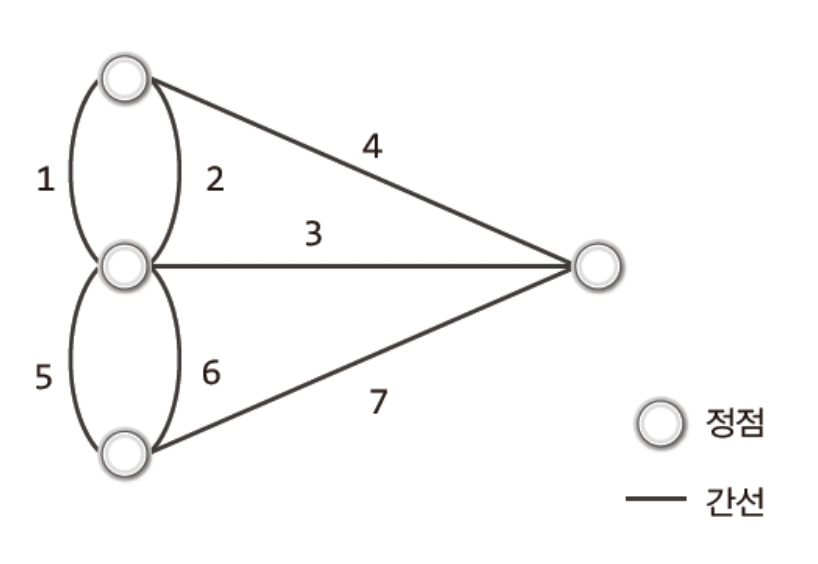
다리 그림의 땅은 정점, 다리는 간선이다.
이렇듯 그래프는 이러한 용어를 사용한다.
그래프의 이해와 종류
그래프 에는 방향성이 있는 그래프와 없는 그래프가 있다.
우선 무방향 그래프 부터 확인하자.

그냥 정점(vertex)이 간선(edge)에 의해 연결되있으나 방향성이 없다
이에 반해서
방향 그래프는
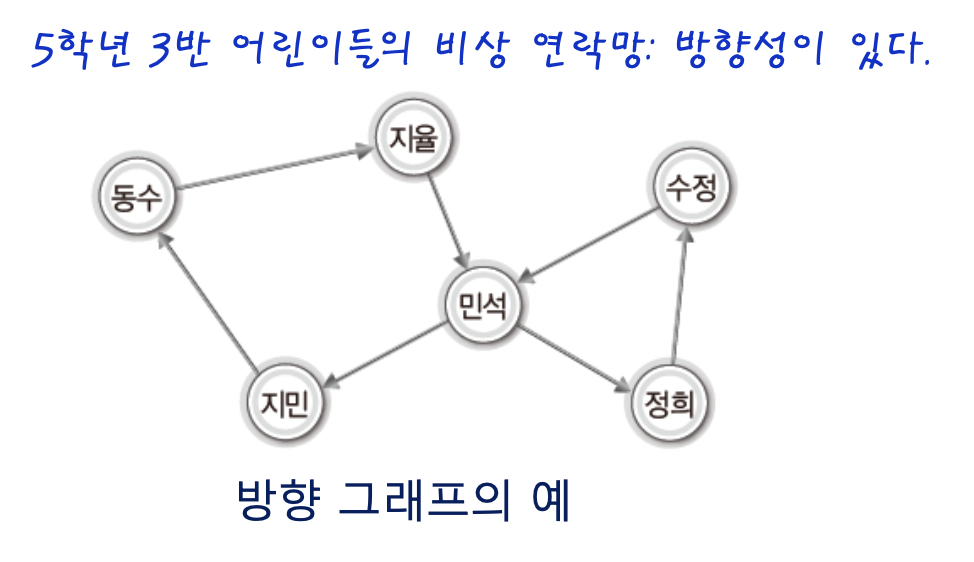
방향이 있다.
이를 두고 방향 그래프 또는 다이그래프라고한다.
이러한 방향/무방향 그래프의 간선의 연결형태에 따라 완전그래프로 구분이 되는데

이렇듯
"각각의 정점에서 다른 모든 정점을 연결한 그래프"
를 뜻한다.
방향 그래프는 그림에서 보이듯 무방향 그래프의 간선의 수에 두 배가 된다.
가중치 그래프와 부분 그래프

가중치 그래프는 이렇듯 어떠한 기준에 가중치를 두어서 간선에 가중치 정보를 매기는것이다.
이 그림에서는 걸리는 시간에 가중치를 주었다.
그렇기에 A->C로 가는 가장 빠른 길을 찾는다면, A->B->C 이다.
그리고 부분집합은
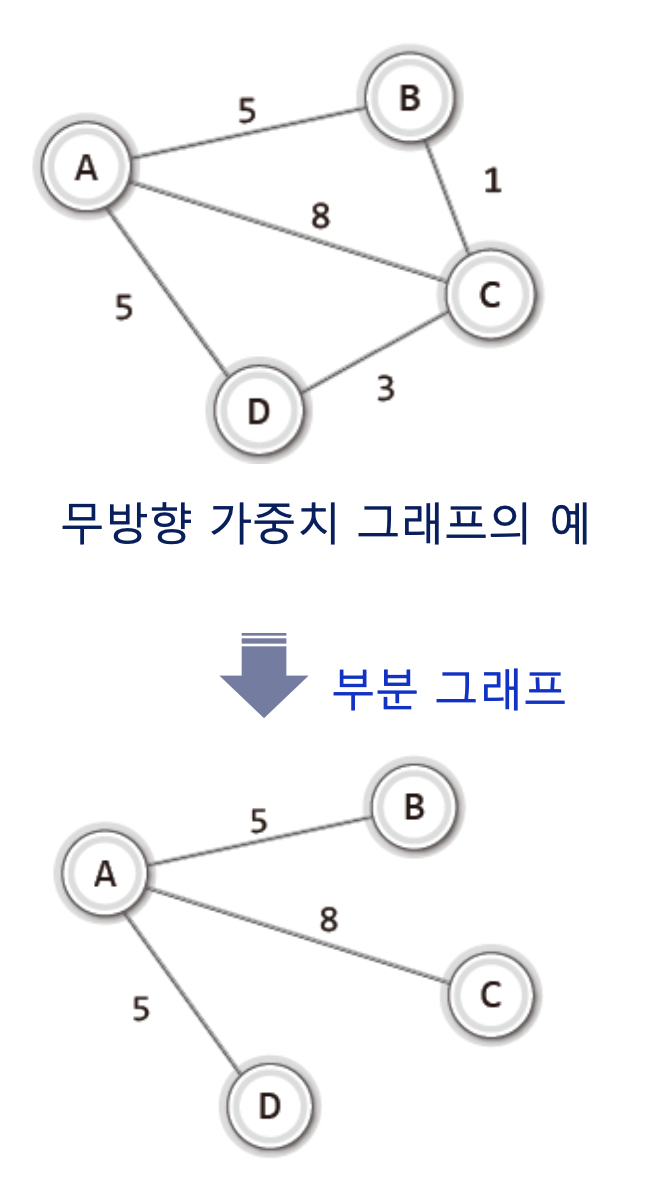
이렇듯 그저! 원 그래프를 구성하는 정점과 간선의 일부로 이뤄진 그래프이다.
그래프의 집합 표현
그래프는 정점과 간선의 집합이기에 집합의 표기법을 이용해서 표현할 수 있다.
그래프의 정점집합과 간선 집합을 나눠서 표현한다.
먼저 !
무방향 그래프 표기법 부터보자!
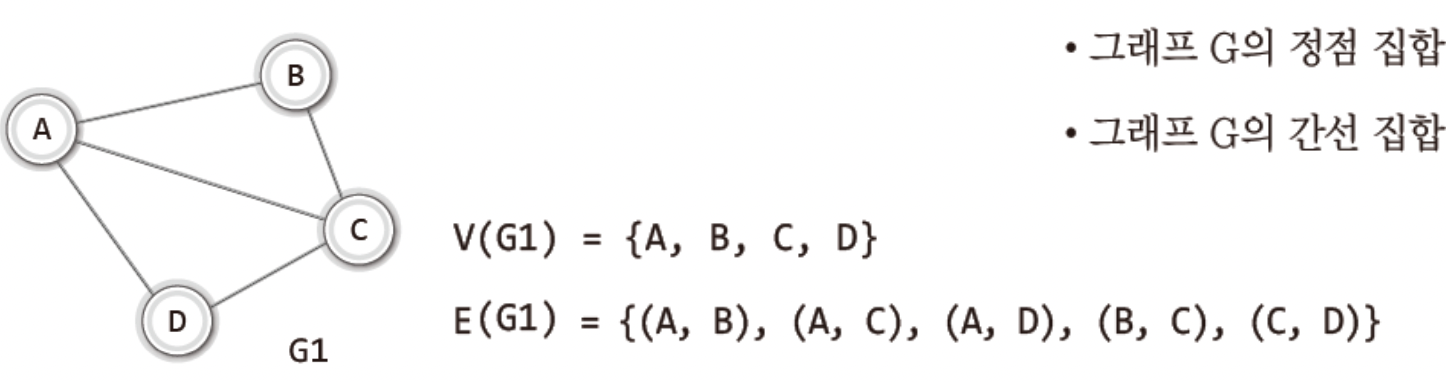
이렇듯 무방향에서 간선에는 방향성이 없으므로
(A,B) 나(B,A)는 동일하다.
반면 방향 그래프에는 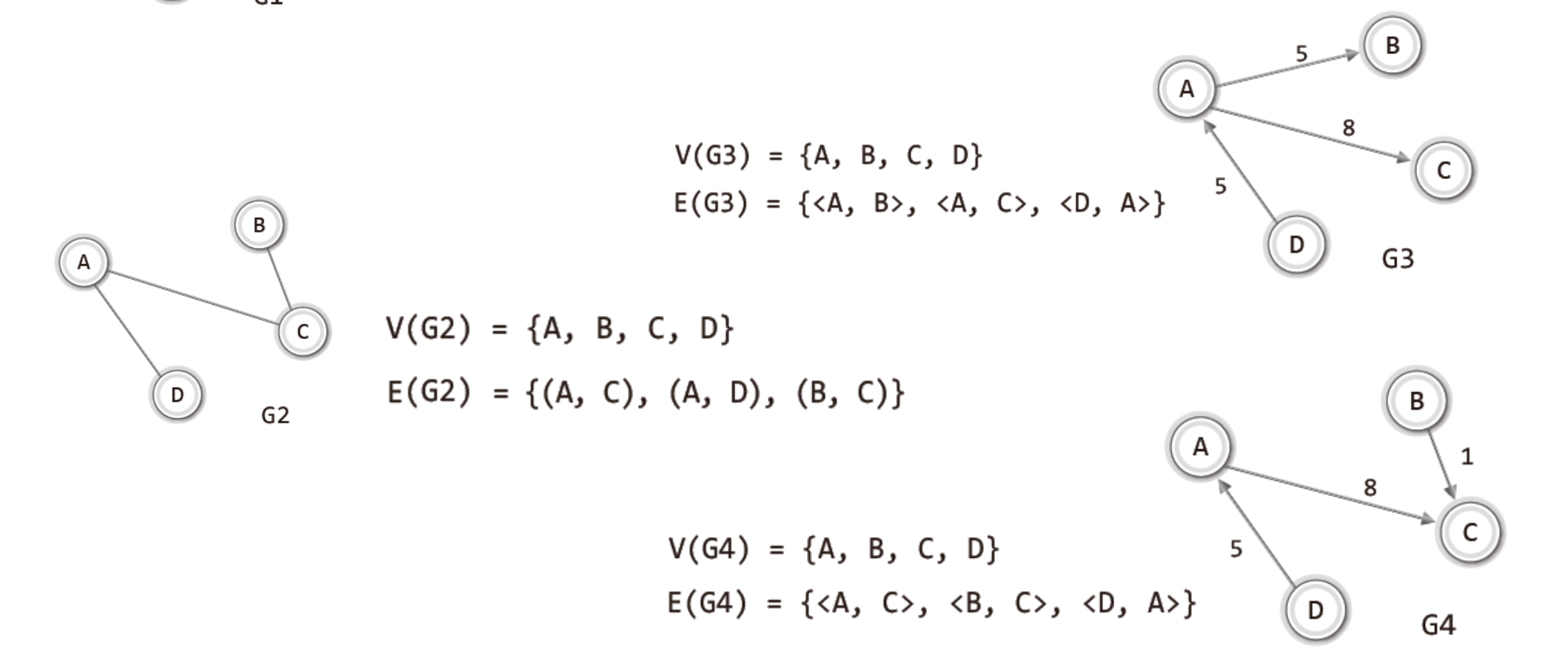
이와 같이 방향성이 있고 A->B 는<A,B> 와 같이 표현된다.
그래프의 ADT
그럼 이제 그래프의 구현을 고민해보자!
우선 ADT를 정의할것인데
구성이 최종 목표라면
"그래프를 생성 및 초기화 할 때 간선의 방향성 여부를 선택할 수 있고, 가중치 부여, 그리고 이후에 얼마든지 언제든지 정점과 간선을 삽입 및 삭제 할수 있다."
정도의 ADT를 기대하겠지만
우리는 구성이 실질적 목표가 아니기에
구성을 위한 필요한만큼의 제한적ADT 를 정의한다.
구성 이후에 주제에 더 관심을 두어야 하기 때문이다!!!
그래프 자료구조의 ADT
Operation:
void GraphInit(UALGraph * pg, int nv);
- 그래프의 초기화를 진행
- 두 번째 인자로 정점의 수를 전달
void GraphDestroy(UALGraph * pg);
- 그래프 초기화 과정에서 할당된 리소스를 반환한다.
void ADDEdge(UALGraph * pg, int fromV, int toV);
- 매개 변수 fromV,toV로 전달된 정점을 연결하는 간선을 그래프에 추가한다.
void ShowGraphEdgeInfo(UALGraph * pg);
- 그래프의 간선정보를 출력한다.
위의 ADT를 보면 정점에 이름을 어떻게 부여해서 AddEge 함수에 어떻게 전달해야할지 궁금증이 들것이다.
그 방법은
열거형 상수를 헤더파일에 다음과 같이 선언한다.
enum {A,B,C---- , I,J}; // 정점의 이름그래서 Init함수에 5가 전달되면 ABCDE 로 이뤄진 그래프가 형성 될 것이다.
그래프를 구현하는 두 가지 방법
그래프도 배열/연결 리스트 이용하는 방법으로 나뉜다.
하지만!
그래프에서는 이들 각각을 다음과 같이 표현한다.
- 인접 행렬 기반 그래프 : 정방 행렬 활용
- 인접 리스트 기반 그래프 : 연결 리스트를 활용
정방 행렬은 가로세로의 길이가 같은 행렬을 의미하는데..
이러한 행렬은 2차원 배열로 표현한다.
즉!! 위에서 말하는 정방 행렬은 이차원 배열을 말하는 것이다.
그럼 먼저 무방향 인접 행렬 기반 그래프를 보자.
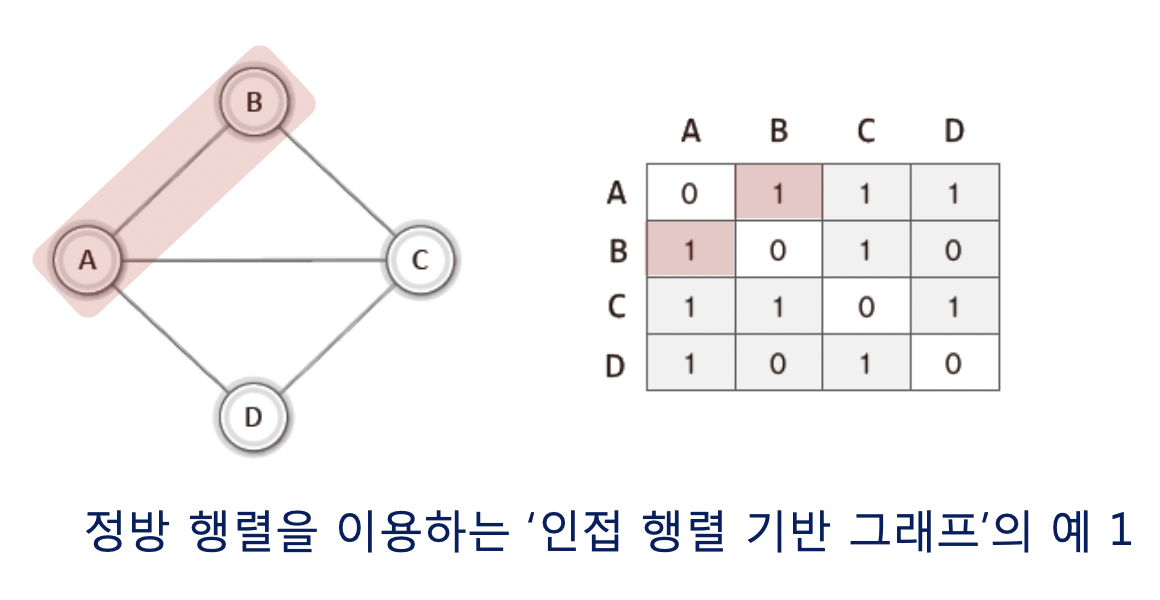
정점이 연결되있으면1 아니면 0으로 기록된다.
어떤가 방향이 없으니 당연 빠따로 대각선을 기준으로 대칭을 이룬다.

그와 다르게 방향 그래프의 인접 행렬 표현은 대칭을 이루지 않는다.
이제 인접 리스트 기반 그래프를 보자!
이 또한 무방향 부터 보자
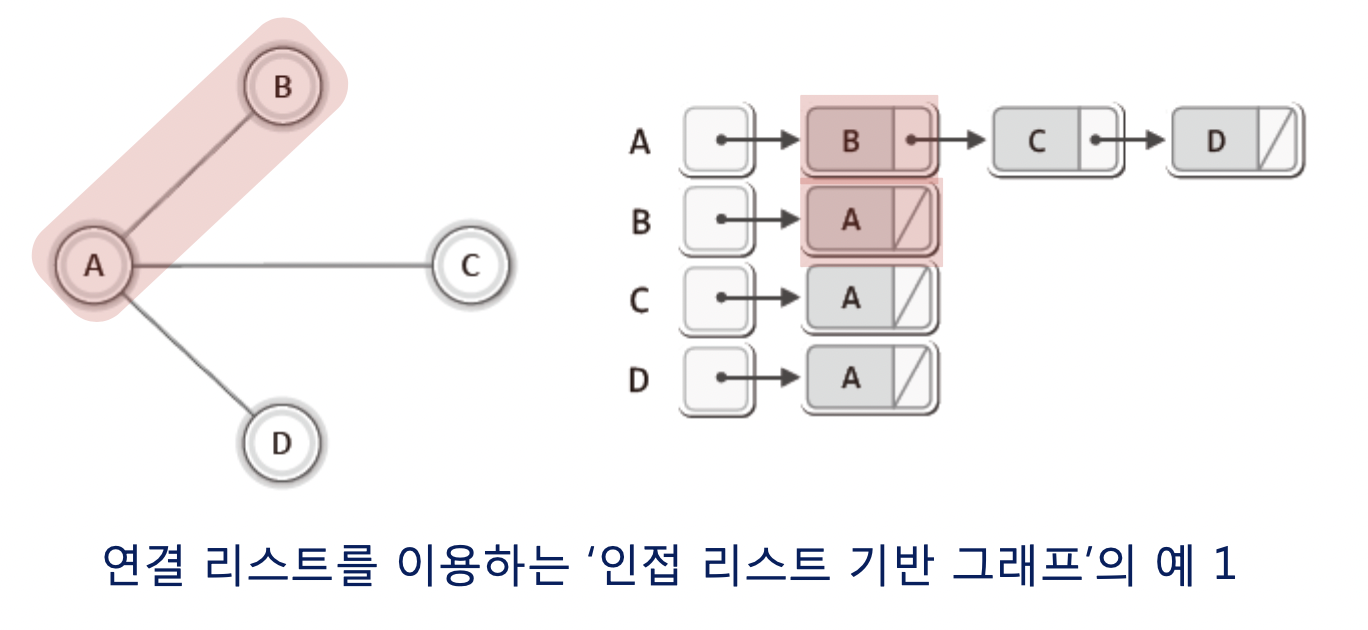
위 그림에서 보이듯이 자신과 연결된 정점의 정보를 담기 위해서 하나의 연결 리스트를 갖는다.
그리고 각각 정점에 연결된 간선의 정보는 각각의 연결 리스트에 담아야한다.
이제 방향이 추가된것을 보자 . 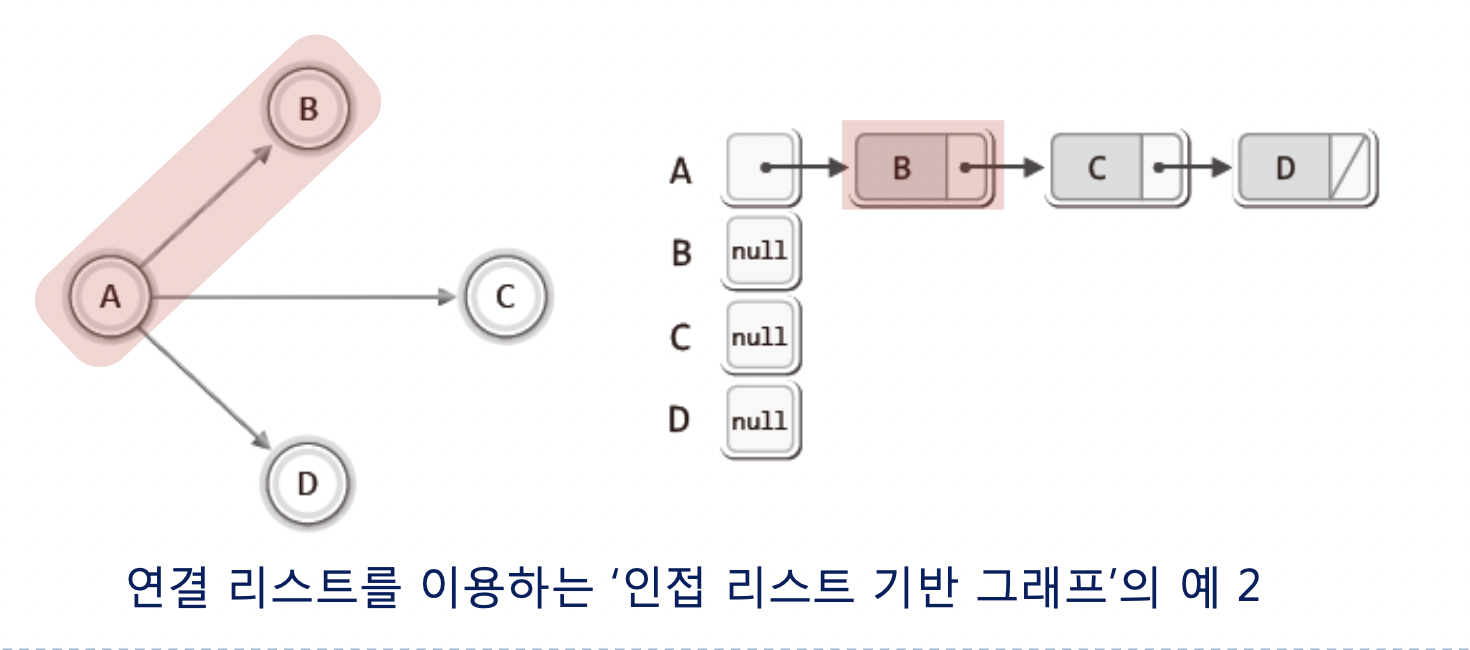
여기에는 각 정점 별로 가리키는 정점의 정보만을 연결 리스트에 담는다.
이제 다음포스트에 구현해보자 !

