[자료구조] 그래프 - 2(인접 리스트 기반의 그래프 구현)

구현 해보일것인데 우리는 인접 리스트 기반의 그래프를 구현해보자.
그 중 무방향 그래프를 할것인데 그 이유는 방향 보다 연결 리스트에 추가해야 하는 노드의 수가 두 배 더 많기 때문이다.

자 ! 바로 헤더파일을 정의해보자
ALgraph.h

//
//  ALGraph.h
//  Graph
//
//  Created by 서희찬 on 2021/04/23.
//

#ifndef ALGraph_h
#define ALGraph_h

#include "DLinkedList.h"

// 정점의 이름을 상수화
enum {A,B,C,D,E,F,G,H,I,J};

typedef struct _ual
{
    int numV; // 정점의 수
    int numE; // 간선의 수
    List * adjList; //간선의 정보
}ALGraph;

// init graph
void GraphInit(ALGraph * pg, int nv);

// 그래프 리소스 해제
void GraphDestroy(ALGraph * pg);

// 간선의 추가
void AddEdge(ALGraph * pg, int fromV, int toV );

// 간선의 정보 출력
void ShowGraphEdgeInfo(ALGraph * pg);

#endif /* ALGraph_h */

이 중

enum {A,B,C,D,E... } 열거형인데 정점의 이름을 상수화 해주는것이다.
즉
A = 0
B= 1 C = 2,D=3.... 이런식으로 말이다.
그래서 AddEdge 에서 int 형으로 받을 수 있는것이다.

그럼 바로 main 함수를 보여주겠다.

#include <stdio.h>
#include "ALGraph.h"

int main(void)
{
    ALGraph graph;// 그래프의 생성
    GraphInit(&graph, 5); // 그래프의 초기화
    
    AddEdge(&graph, A, B); // A B 연결
    AddEdge(&graph, A, D);
    AddEdge(&graph, B, C);
    AddEdge(&graph, C, D);
    AddEdge(&graph, D, E);
    AddEdge(&graph, E, A);
    
    ShowGraphEdgeInfo(&graph); // 그래프의 간선정보 출력
    GraphDestroy(&graph); // 그래프의 리소스 소멸
    
    return 0;
}

어떤 방식으로 함수들이 정의 되어야하는지 메인 함수를 보고 나니 어림잡을 수 있겠는가?
이런 그래프가 생성될것이다.

이제 AVLGraph.c 를 구현해보자 !

먼저 Intit 함수부터 보자.

void GraphInit(ALGraph * pg, int nv) // 그래프의 초기화
{
    int i;
    
    // 정점의 수에 해당하는 길이의 리스트 배열을 생성하낟.
    pg->adjList = (List*)malloc(sizeof(List)*nv); // 간선정보를 저장할 리스트 생성
    
    pg->numV = nv; // 정점의 수는 nv에 저장된 값으로 결정
    pg->numE=0;// 초기의 간선수는 0개
    
    // 정점의 수만큼 생성된 리스트들을 초기화한다.
    for(i=0;i<nv;i++)
    {
        ListInit(&(pg->adjList[i]));
        SetSortRule(&(pg->adjList[i]), WhoIsPrecede); 정렬기준유도
        
    }
}

마지막 문장은 알파벳 순으로의 출력을 위한 정렬기준을 설정한것이다.

그림 GraphDestroy 함수가 왜 필요한지 알겠는가?

void GraphDestroy(ALGraph * pg)
{
    if(pg->adjList != NULL)
        free(pg->adjList); // 동적으로 할당된 연결 리스트의 소멸
}

할당을 해주었으니 소멸해준것이다.

이제 AddEdge 함수를 보자 .

이 함수의 정의를 통해서 간선의 이름이 지니는 상수 값의 의미또한 파악하자!

void AddEdge(ALGraph * pg, int fromV, int toV )
{
    // 정점 form V의 연결 리스트에 정점 toV 의 정보 추가
    LInsert(&(pg->adjList[fromV]), toV);
    
    // 정점 toV의 연결 리스트에 정점 fromV의 정보 추가
    LInsert(&(pg->adjList[toV]), fromV);
    pg->numE+=1;
    
}

무방향 그래프의 간선 추가이므로 LInsert 함수를 두 번 호출하였다.
만약 방향 그래프 였다면 한번만 추가해도 됐다.

또한 연결 리스트의 인덱스값으로 toV fromV 가 사용됐음을 주목하자!!

이렇듯 정점의 이름이 바로 사용될 수 있는 이유는, 정점의 이름이 의미하는 바가 상수이고, 그 값이 0에서 부터 시작해서 1씩 증가하기 때문이다.

그럼 어느정도의 기능들을 정의해서 알아봤으니 전체 소스코드를 보여주겠다

ALGraph.c

//
//  ALGraph.c
//  Graph
//
//  Created by 서희찬 on 2021/04/23.
//
#include <stdio.h>
#include <stdlib.h>
#include "DLinkedList.h"
#include "ALGraph.h"

int WhoIsPrecede(int data1,int data2);

void GraphInit(ALGraph * pg, int nv) // 그래프의 초기화
{
    int i;
    
    // 정점의 수에 해당하는 길이의 리스트 배열을 생성하낟.
    pg->adjList = (List*)malloc(sizeof(List)*nv); // 간선정보를 저장할 리스트 생성
    
    pg->numV = nv; // 정점의 수는 nv에 저장된 값으로 결정
    pg->numE=0;// 초기의 간선수는 0개
    
    // 정점의 수만큼 생성된 리스트들을 초기화한다.
    for(i=0;i<nv;i++)
    {
        ListInit(&(pg->adjList[i]));
        SetSortRule(&(pg->adjList[i]), WhoIsPrecede); //정렬기준유도
        
    }
    
}

void GraphDestroy(ALGraph * pg)
{
    if(pg->adjList != NULL)
        free(pg->adjList); // 동적으로 할당된 연결 리스트의 소멸
}

void AddEdge(ALGraph * pg, int fromV, int toV )
{
    // 정점 form V의 연결 리스트에 정점 toV 의 정보 추가
    LInsert(&(pg->adjList[fromV]), toV);
    
    // 정점 toV의 연결 리스트에 정점 fromV의 정보 추가
    LInsert(&(pg->adjList[toV]), fromV);
    pg->numE+=1;
    
}

void ShowGraphEdgeInfo(ALGraph * pg)
{
    int i;
    int vx;
    
    for (i=0; i<pg->numV; i++) {
        printf("%c 와 연결된 정점 : ",i + 65); // 아스키코드로 !
        
        if(LFirst(&(pg->adjList[i]), &vx))
        {
            printf("%c ",vx+65);
            
            while(LNext(&(pg->adjList[i]), &vx))
                printf("%c ",vx+65);
        }
        printf("\n");
    }
}

int WhoIsPrecede(int data1, int data2)
{
    if(data1<data2)
        return 0;
    else
        return 1;
}

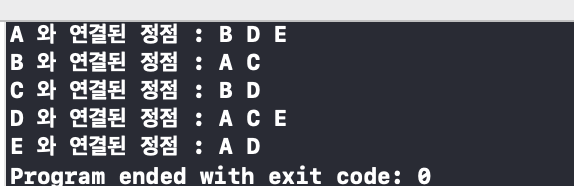
성공적으로 출력이 완료된다.